Capítulo 10 Redes Metabólicas
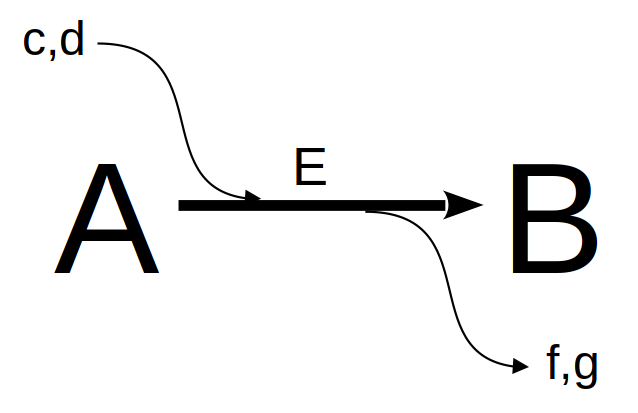
Figura 10.1: Uma representação da caixa preta de reações enzimáticas. E = enzima c,d = cofatores, coenzimas, modificadores; f,g = compostos secundários resultantes da catálise .
Algumas equações diferenciais podem ser analiticamente resolvidas, como as que envolvem o crescimento exponencial bacteriano:
10.1 Solução numérica para sistema de equações diferenciais
R (deSolve,pracma, lsoda), alguns sistemas simples podem ser resolvidos com os pacotes básicos de instalação:O procedimento mais simples emprega o método de Euler. A ideia básica do método consiste em integrar uma função diferencial de variação infinitesimal na variável independente (no caso, o tempo), para uma relação real, e a partir de valores iniciais fornecidos. Simplificando, o valor da função corresponderá ao acréscimo do incremento dy para cada intervalo dx, a partir da relação de cada reação envolvida na transformação dos compostos. Exemplificando para as reações presentes na Eq. (10.4):
k = 0.5 # constante cinética de catálise
dt = .005; tmax = 3 # intervalo de tempo & tempo máximo
t = seq(0,tmax,dt) # vetor de tempo
n = tmax/dt+1 # no. de pontos da simulação (necessário o acréscimo de 1 para que vetores fiquem de mesmo tamanho)
x = matrix(rep(0,2*n),nrow=2,ncol=n) # construção da matriz de uma linha pra cada composto, e uma coluna pra cada tempo dt
x[1,1] = 1; x[2,1] = 0 # valores iniciais de concentração
for(i in 2:n){
dA = -k*x[1,i-1]*dt; # dA
dB = k*x[1,i-1]*dt; # dB
x[1,i] = x[1,i-1]+dA; # variação em A com acrécimo dA
x[2,i] = x[2,i-1]+dB # variação em B com acréscimo dB
# laço que acrescenta a cada intervalo dt o valor do novo teor para cada composto
}
plot(t,x[1,],type="l",lty=1,
xlab="tempo, s",ylab="[espécie], M",ylim=c(0,1.025),
bty="l") # gráfico do composto 1
lines(t,x[2,],lty=2,col=2) # adição do gráfico do composto 2
legend(x=2,5,y=1,legend=c("A","B"),col=c(1,2),cex=1,
lty=c(1,2))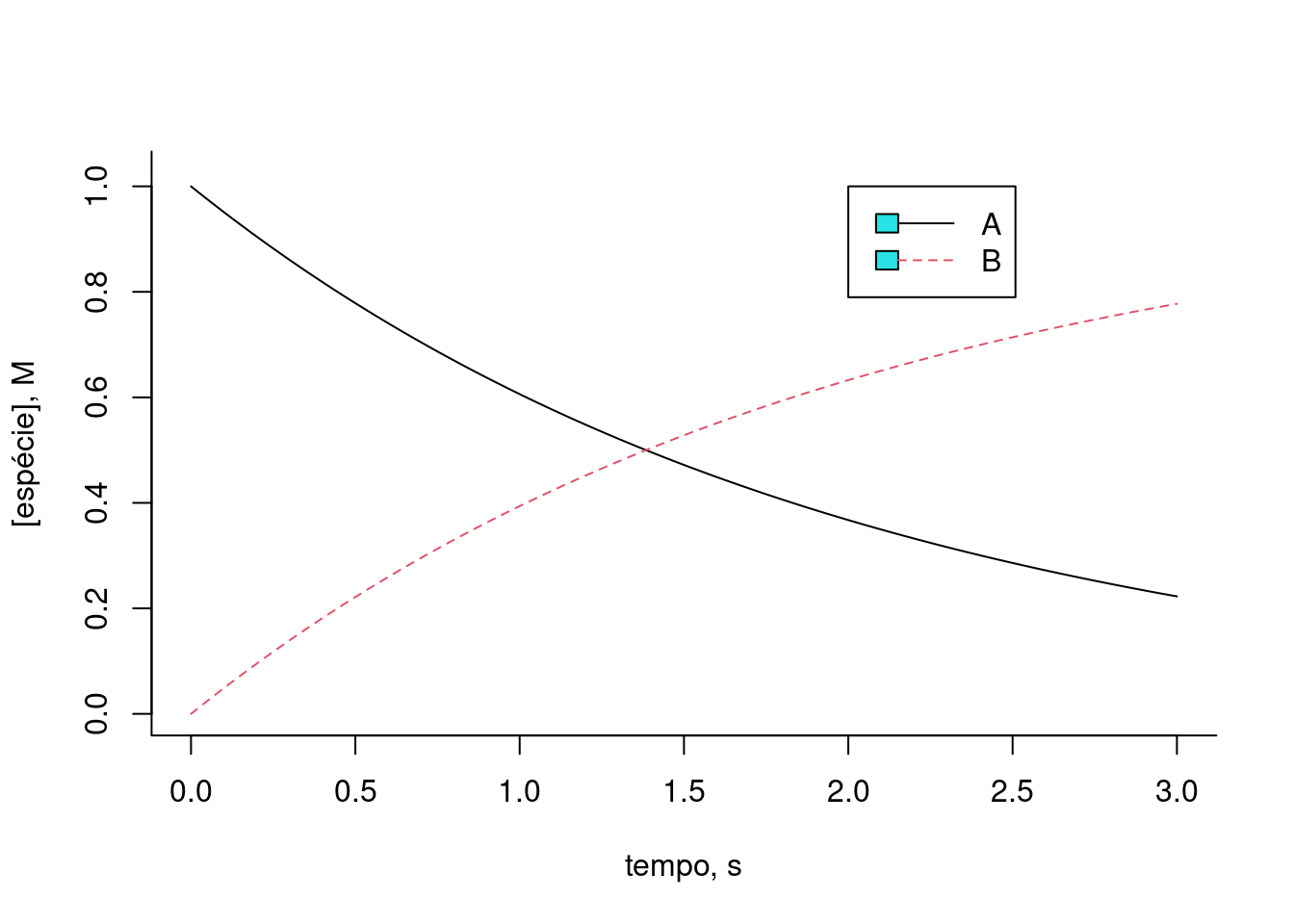
Figura 10.2: Solução de sistema de equações diferenciais por método de Euler para conversão de 1a. ordem da espécie A em B, a uma taxa cinética k.
R:k = 0.5; km = 0.5 # constantes cinéticas de catálise
dt = .005; tmax = 10 # intervalo de tempo & tempo máximo
t = seq(0,tmax,dt) # define vetor de tempo
n = tmax/dt+1 # define no. de pontos
x = matrix(rep(0,2*n),nrow=2,ncol=n) # constroi matriz de uma linha pra cada composto, e uma coluna pra cada tempo dt
x[1,1] = 1; x[2,1] = 1 # valores iniciais de concetração
for(i in 2:n){
dA = -k*x[1,i-1]*dt+km*x[2,i-1]*dt;
dB = k*x[1,i-1]*dt-km*x[2,i-1]*dt;
x[1,i] = x[1,i-1]+dA;
x[2,i] = x[2,i-1]+dB;
# laço que acrescenta a cada intervalo dt o valor de novo teor para cada composto
}
plot(t,x[1,],type="l",lty=1,
xlab="tempo, s",ylab="[espécie], M",ylim=c(0,2),bty="l") # gráfico do composto 1
lines(t,x[2,],lty=2,col=2) # adição do gráfico do composto 2
legend(x=2,5,y=2,legend=c("A","B"),col=c(1,2),cex=1,
lty=c(1,2))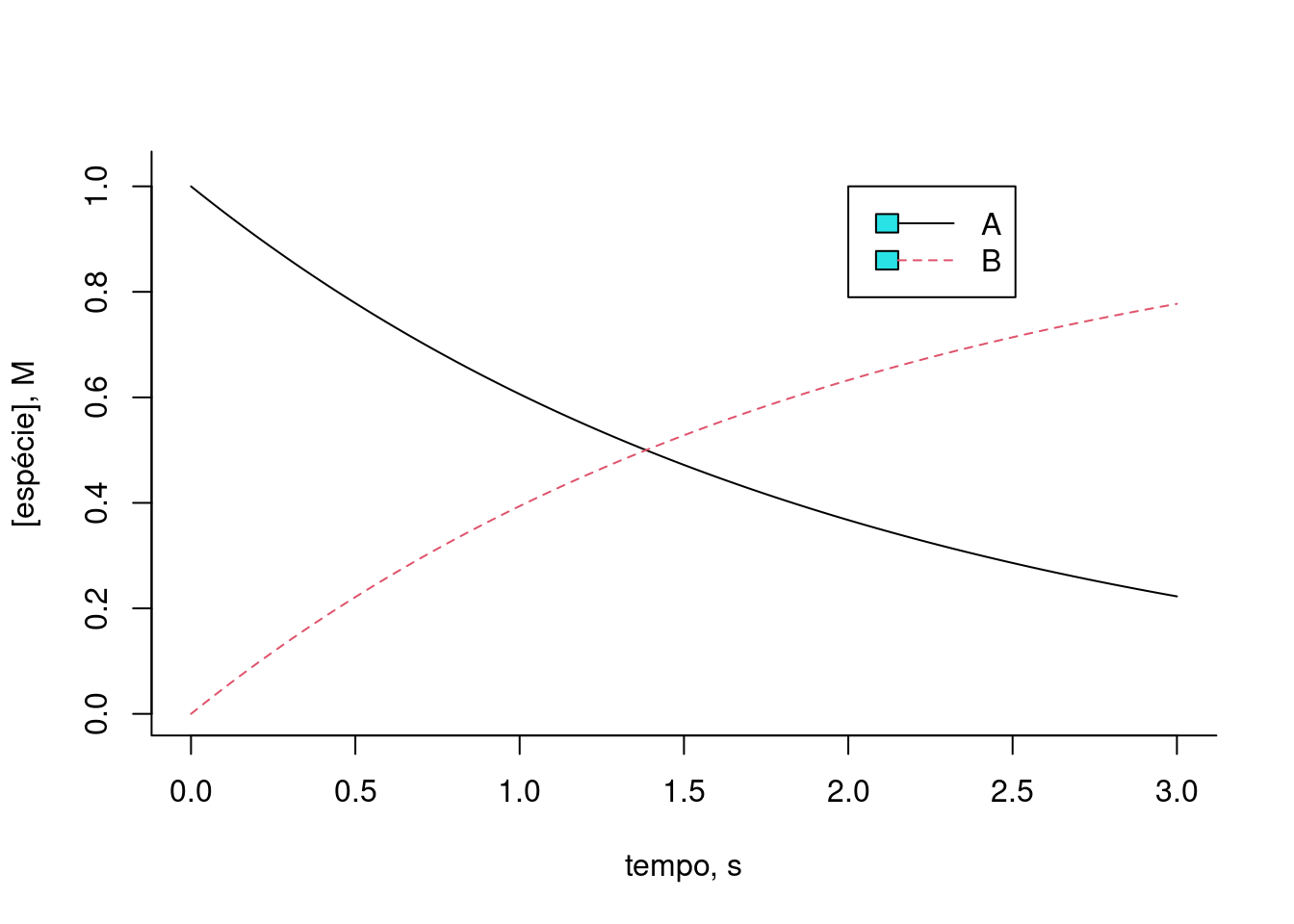
Figura 10.3: Solução numérica para a conversão reversível da espécie A em B. k = km = 0,5; Ao e Bo = 1 (teores iniciais).
k = 0.5; km = 0.1 # constantes cinéticas de catálise
dt = .005; tmax = 10 # intervalo de tempo & tempo máximo
t = seq(0,tmax,dt) # define vetor de tempo
n = tmax/dt+1 # define no. de pontos
x = matrix(rep(0,2*n),nrow=2,ncol=n) # constroi matriz de uma linha pra cada composto, e uma coluna pra cada tempo dt
x[1,1] = 1; x[2,1] = 0.2 # valores iniciais de concetração
for(i in 2:n){
dA = -k*x[1,i-1]*dt+km*x[2,i-1]*dt;
dB = k*x[1,i-1]*dt-km*x[2,i-1]*dt;
x[1,i] = x[1,i-1]+dA;
x[2,i] = x[2,i-1]+dB;
# laço que acrescenta a cada intervalo dt o valor de novo teor para cada composto
}
plot(t,x[1,],type="l",lty=1,
xlab="tempo, s",ylab="[espécie], M",ylim=c(0,2),bty="l") # gráfico do composto 1
lines(t,x[2,],lty=2,col=2) # adição do gráfico do composto 2
legend(x=2,5,y=2,legend=c("A","B"),col=c(1,2),cex=1,lty=c(1,2))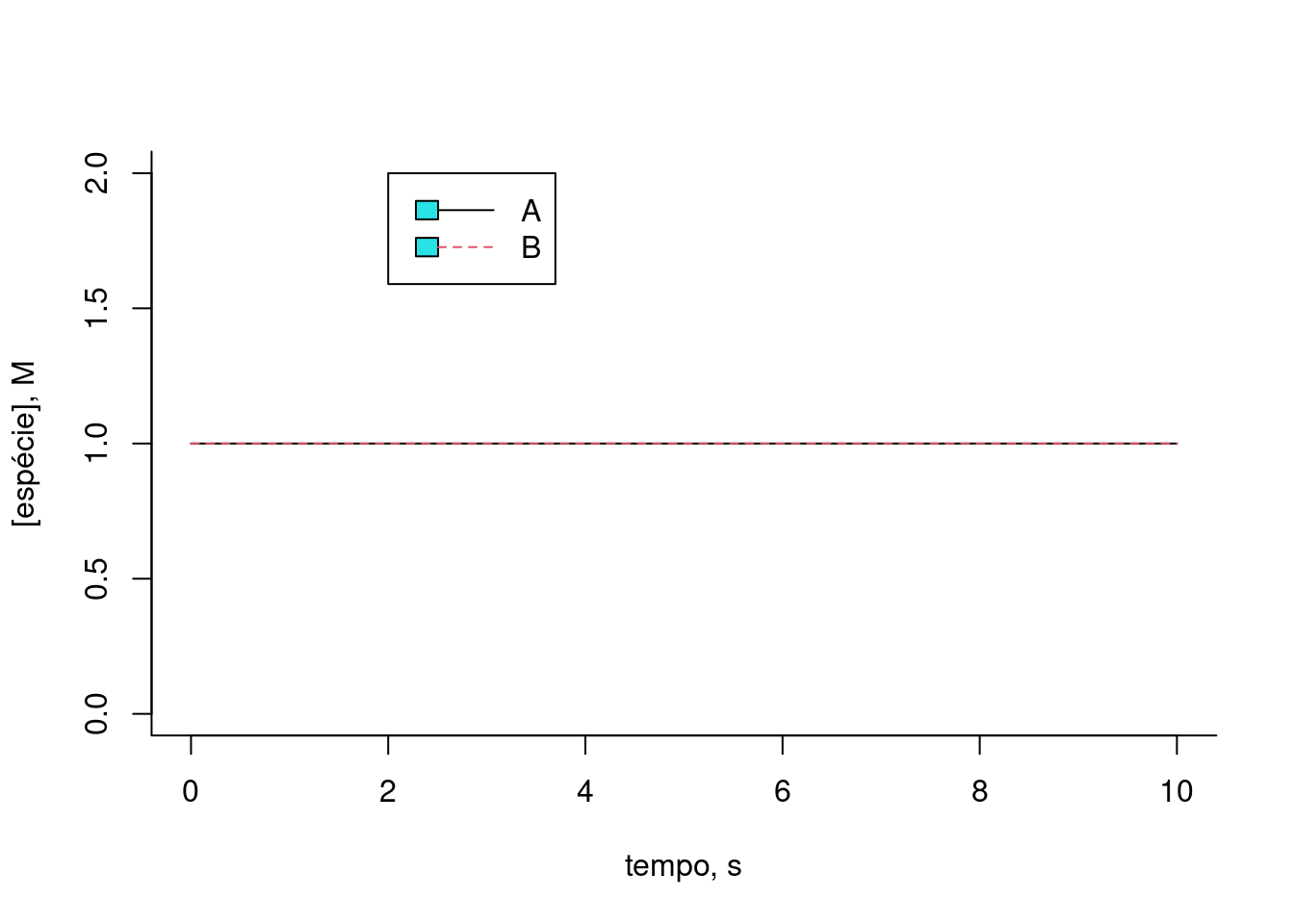
Figura 10.4: Solução numérica para a conversão reversível da espécie A em B. k = 0,5; km = 0,1; Ao = 1; Bo = 0,2 (teores iniciais).
k1 = 0.5; km1 = 0.1; k2 = 1 # constantes cinéticas de catálise
dt = .005; tmax = 3 # intervalo de tempo & tempo máximo
t = seq(0,tmax,dt) # define vetor de tempo
n = tmax/dt+1 # define no. de pontos
x = matrix(rep(0,3*n),nrow=3,ncol=n) # constroi matriz de uma linha pra cada composto, e uma coluna pra cada tempo dt
x[1,1] = 1; x[2,1] = 0; x[3,1] = 0 # valores iniciais de concentração
for(i in 2:n){
dA = -k1*x[1,i-1]*dt+km1*x[2,i-1]*dt;
dB = k1*x[1,i-1]*dt-(km1+k2)*x[2,i-1]*dt;
dC = k2*x[2,i-1]*dt;
x[1,i] = x[1,i-1]+dA;
x[2,i] = x[2,i-1]+dB;
x[3,i] = x[3,i-1]+dC; # laço que acrescenta a cada intervalo dt o valor de novo teor para cada composto
}
plot(t,x[1,],type="l",lty=1,
xlab="tempo, s",ylab="[espécie], M",ylim=c(0,1.025),bty="l") # gráfico do composto 1
lines(t,x[2,],lty=2,col=2) # adição do gráfico do composto 2
lines(t,x[3,],lty=3,col=3) # adição do gráfico do composto 3
legend(x=2,5,y=1,legend=c("A","B","C"),col=c(1,2,3),cex=1,lty=c(1,2,3))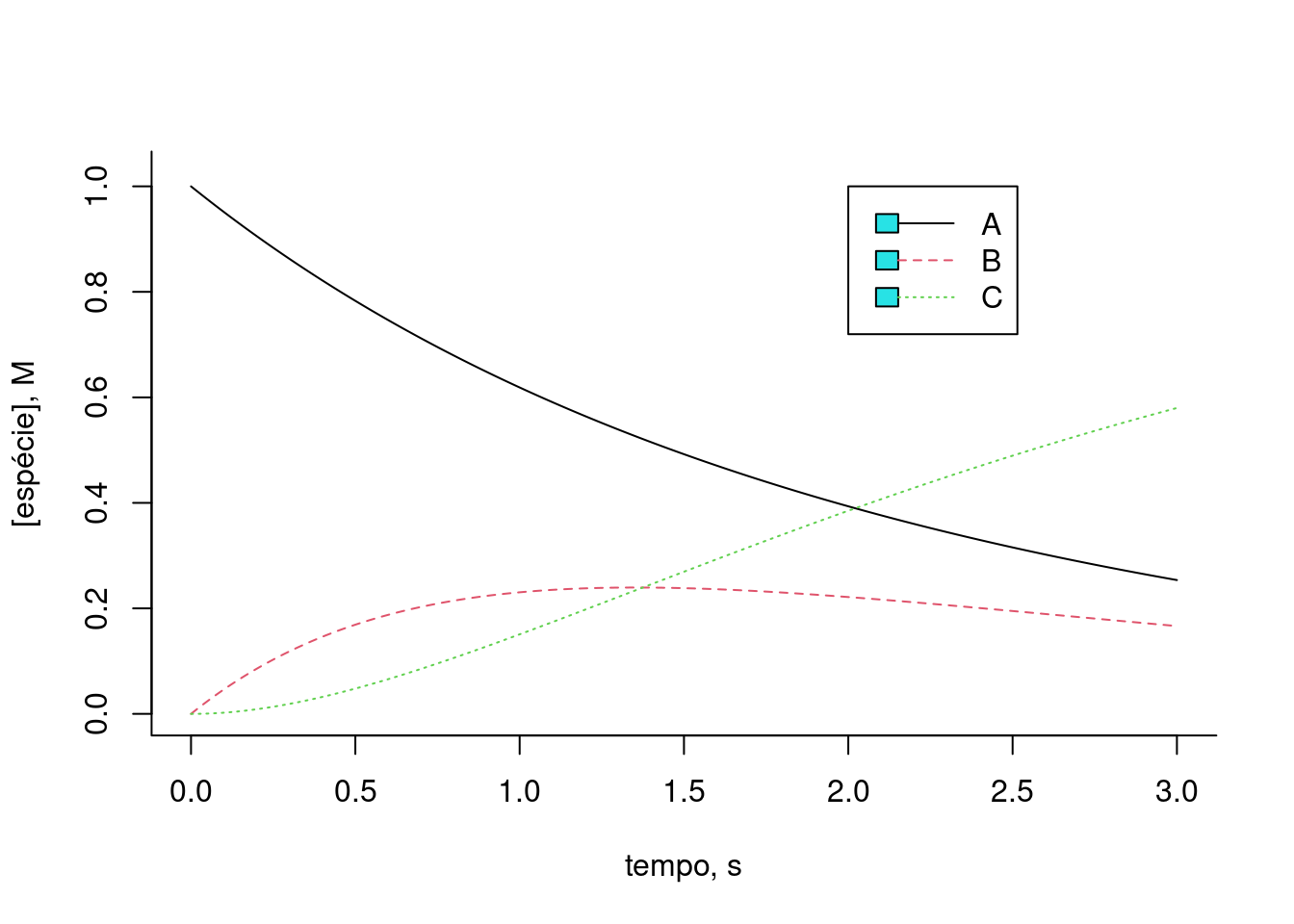
Figura 10.5: Solução de Euler para uma cinética de 3 compostos. k1 = 0,5; k2 = 1; km1 = 0,1. Teores iniciais: Ao = 1; Bo = 0; Co = 0.
R: # Forward and reverse rate constants
k1 = 3; km1 = 1; k2 = 4; km2 = 0.7
dt = .005; tmax = 10
t = seq(0,tmax,dt); n = tmax/dt+1
x = matrix(rep(0,3*n),nrow=3,ncol=n)
x[1,1] = 1; x[2,1] = 0; x[3,1] = 0
for(i in 2:n){
dA = -k1*x[1,i-1]*dt+km1*x[2,i-1]*dt;
dB = k1*x[1,i-1]*dt-(km1+k2)*x[2,i-1]*dt+
km2*x[3,i-1]*dt;
dC = k2*x[2,i-1]*dt-km2*x[3,i-1]*dt;
x[1,i] = x[1,i-1]+dA;
x[2,i] = x[2,i-1]+dB;
x[3,i] = x[3,i-1]+dC;
}
plot(t,x[1,],type="l",lty=1,
xlab="tempo, s",ylab="[espécie], mol/L"
,ylim=c(0,1.025),bty="l")
lines(t,x[2,],col=2,lty=2)
lines(t,x[3,],col=3,lty=3)
legend(x=8,y=0.6,legend=c("A","B","C"),col=c(1,2,3),cex=1,lty=c(1,2,3))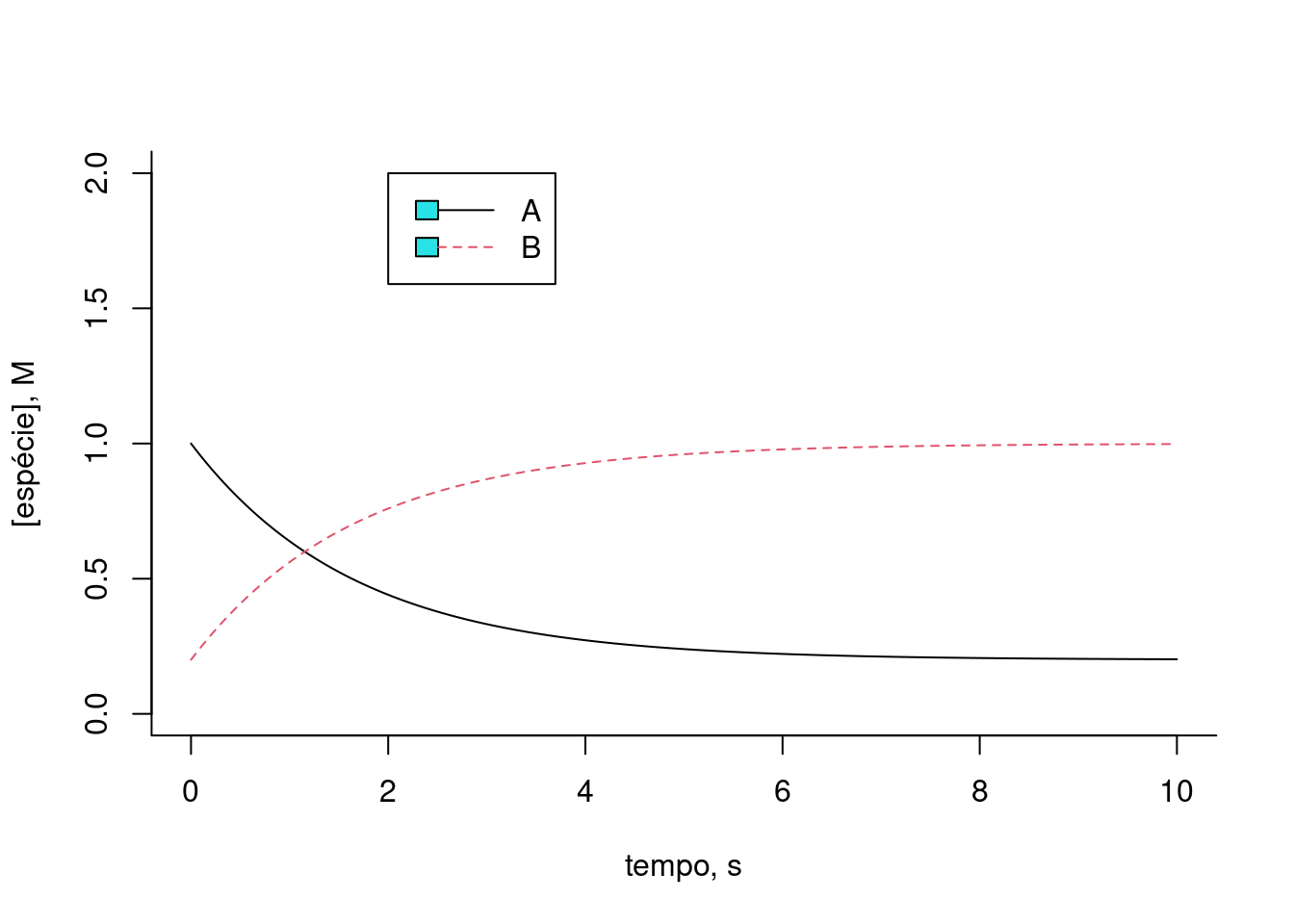
Figura 10.6: Solução de Euler para uma cinética reversível de 3 compostos. k1 = 1; km1 = 3; k2 = 5; km1 = 0,1. Teores iniciais: Ao = 1; Bo = 0; Co = 0.
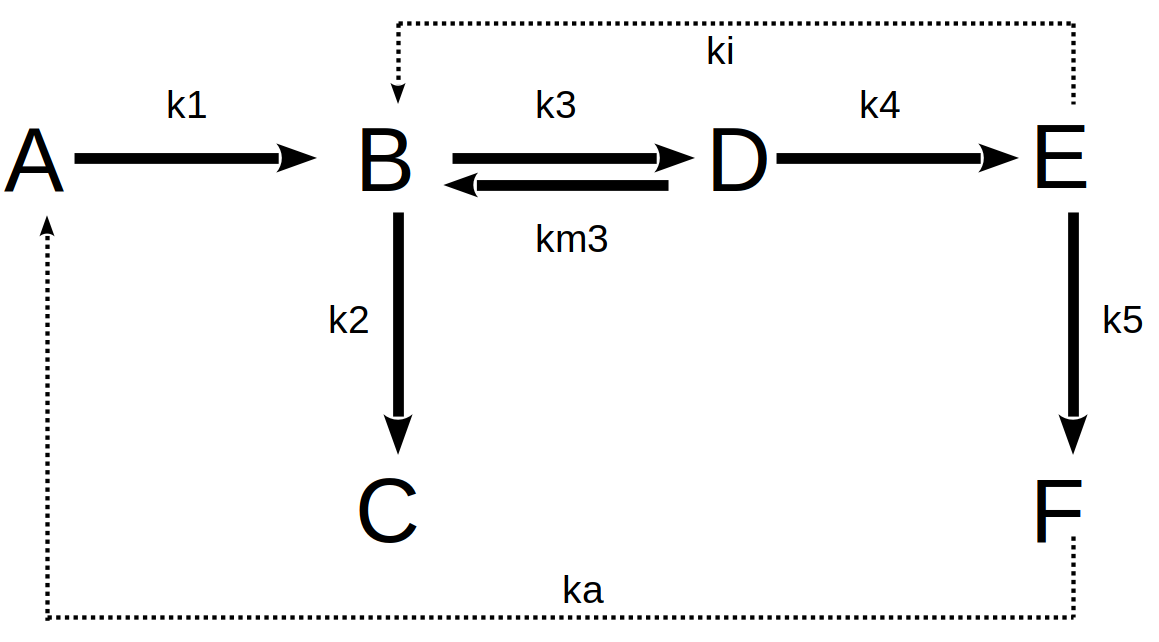
Figura 10.7: Um exemplo de reações bioquímicas em rota metabólica fictícia. As setas pontilhadas juntamente aos valores de ki e ka representam modulações alostéricas com respectivas constantes de inibição e ativação enzimáticas.
Pode-se elaborar o trecho de código que segue para a solução numérica de Euler que envolve as equações diferenciais elencadas acima como:# Constantes cinéticas e alostéricas
k1 = 2
k2 = 0.5
k3 = 0.7
km3 = 0.3
k4 = 5
k5 = 1
ki = 0.3 # constante de inibição
ka = 0.2 # constante de ativação
dt = .005; tmax = 10
t = seq(0,tmax,dt); n = tmax/dt+1
x = matrix(rep(0,6*n),nrow=6,ncol=n)
# Valores iniciais dos compostos
x[1,1] = 1; x[2,1] = 0; x[3,1] = 0; x[4,1] = 1; x[5,1] = 0; x[6,1] = 0
for(i in 2:n){
# sistema de equações inserido na matriz dos intervalos
dA=-k1*x[1,i-1]*dt+ka*x[6,i-1]*dt;
dB=k1*x[1,i-1]*dt+km3*x[4,i-1]*dt-k3*x[2,i-1]*dt-k2*x[2,i-1]*dt-ki*x[1,i-1]*dt;
dC=k2*x[2,i-1]*dt;
dD=k3*x[2,i-1]*dt-km3*x[4,i-1]*dt-k4*x[4,i-1]*dt;
dE=k4*x[4,i-1]*dt-k5*x[5,i-1]*dt;
dF=k5*x[5,i-1]*dt-ka*x[6,i-1]*dt
# Adição dy aos valores de y
x[1,i] = x[1,i-1]+dA;
x[2,i] = x[2,i-1]+dB;
x[3,i] = x[3,i-1]+dC;
x[4,i] = x[4,i-1]+dD;
x[5,i] = x[5,i-1]+dE;
x[6,i] = x[6,i-1]+dF
}
# Elaboração dos gráficos cinéticos
plot(t,x[1,],type="l",lty=1,
xlab="tempo,s",ylab="[espécie], mol/L",ylim=c(0,1.025),bty="l")
lines(t,x[2,],col=2,lty=2)
lines(t,x[3,],col=3,lty=3)
lines(t,x[4,],col=4,lty=4)
lines(t,x[5,],col=5,lty=5)
lines(t,x[6,],col=6,lty=6)
legend(x=6.5,y=0.65,legend=c("A","B","C","D","E","F"),col=c(1,2,3,4,5,6),cex=1,lty=c(1,2,3,4,5,6))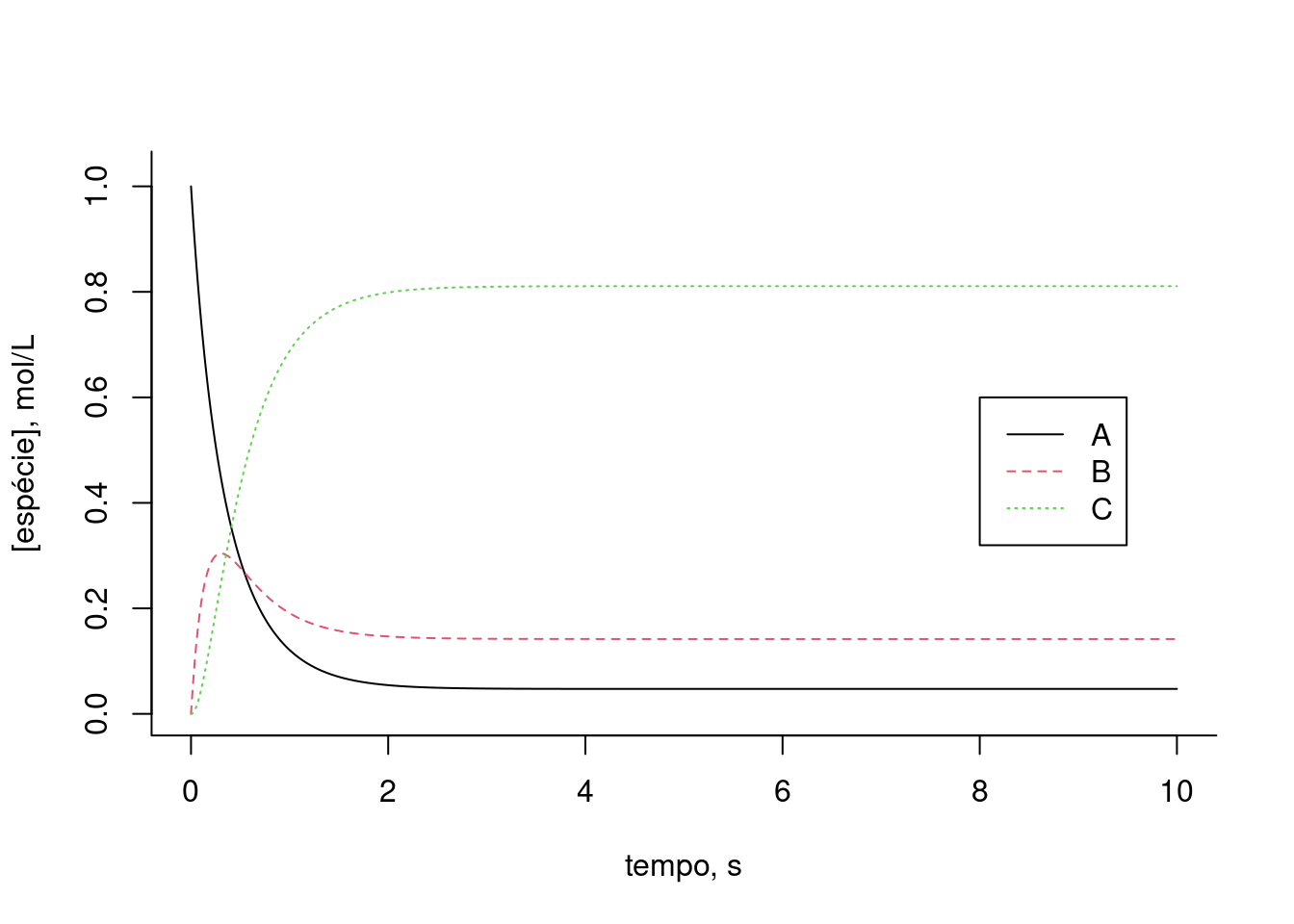
Figura 10.8: Solução para uma via metabólica fictícia apresentando inibição (ki) e ativação (ka) alostéricas. Taxas cinéticas: k1 = 2, k2 = 0,5, k3 = 0,7, km3 = 0,3, k4 = 5, k5 = 1, ki = 0,3, ka = 0.2. Valores iniciais dos compostos: A=1; B, C, D, E, F = 0
R, ou ainda por análise de sistemas.10.2 Algumas reações do metabolismo da glicose
deSolve ou similar para a solução de sistema de equações diferenciais ordinárias de 1a. ordem ou diferenciais parciais. A biblioteca agrega funções que permitem um código mais enxuto e simples para a solução do sistema. Ilustrando sua aplicação, seguem algumas das muitas relações simples da rede metabólica que envolve a glicólise, gliconeogênese, e via das pentoses nas células: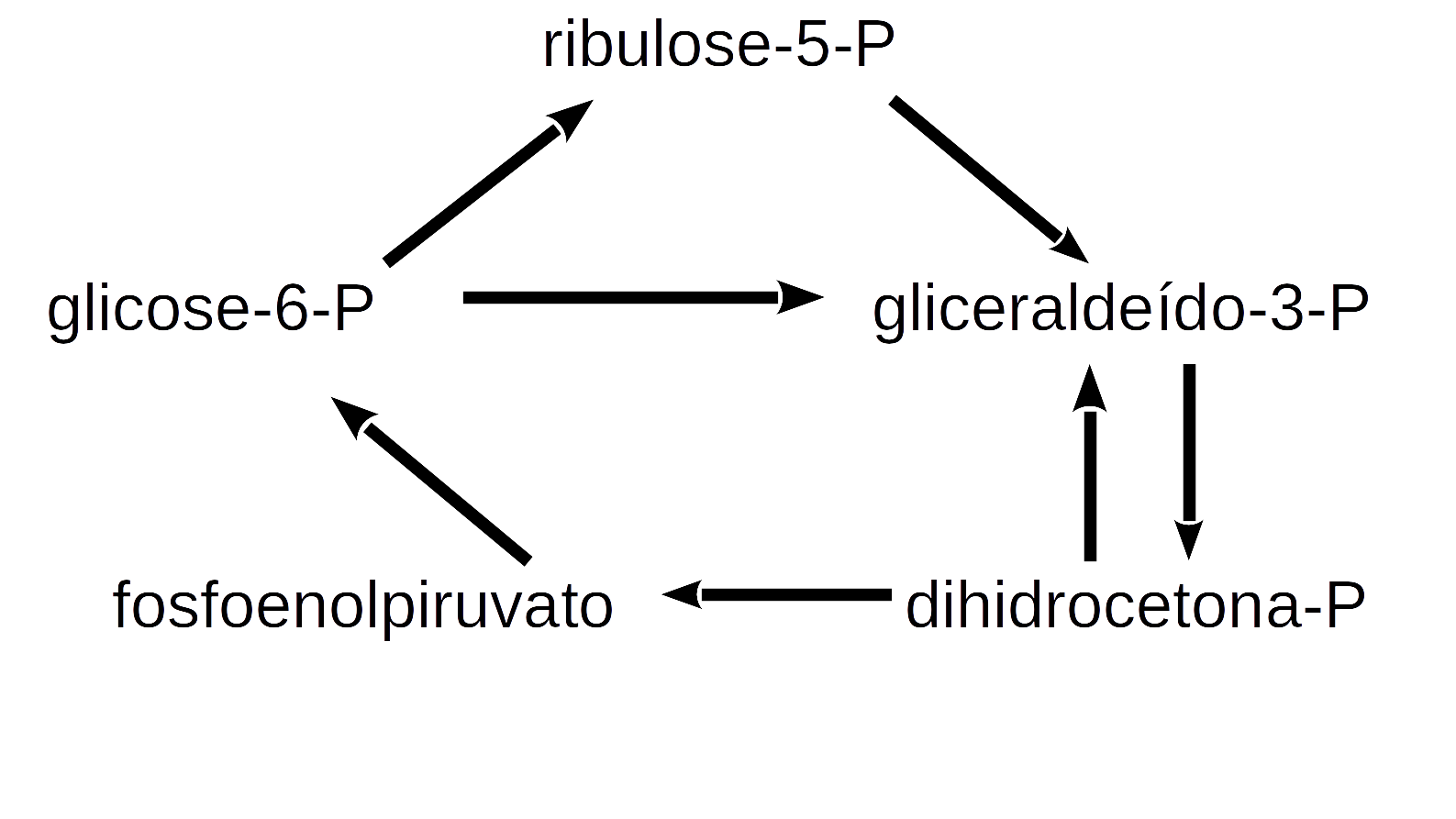
Figura 10.9: Algumas relações metabólicas envolvidas na glicólise, gliconeogênese e vias das pentoses.
library(deSolve)
# Parâmetros das reações
k1 = 0.1; k2 = 0.5; k3 = 0.05; k4 = 0.5; k5 = 0.2
parms = c(k1, k2, k3, k4, k5)
# Valores iniciais para cada composto
G6P0=1;R5P0=0;G3P0=0.3;DHCP0=0.1;PEP0=0
# Intervalo de tempo
tmin = 0; tmax = 20; dt = 0.01
tempo = seq(tmin, tmax, dt)
# Função para as derivadas das espécies no tempo
eq.dif = function(tempo, x, parms) {
# especificação dos compostos
G6P = x[1]
R5P = x[2]
G3P = x[3]
DHCP = x[4]
PEP = x[5]
# equações diferenciais
dG6P = -k1*G6P+k3*G3P^2+k5*PEP^2
dR5P = k1*G6P-k4*R5P
dG3P = -k2*G3P*DHCP-k3*G3P^2+k4*R5P
dDHCP = -k2*G3P*DHCP
dPEP = k2*G3P*DHCP-k5*PEP^2
list(c(dG6P,dR5P, dG3P, dDHCP, dPEP)) # incrementos das espécies
}
# Rotina de lsoda pra solução diferencial ordinária
out = lsoda(c(G6P0,R5P0,G3P0,DHCP0,PEP0),tempo,eq.dif, parms,
rtol=1e-4, atol= 1e-6)
# Saída do resultado em vetores pra cada quantidade (tempo e espécies)
t = out[,1]; G6P = out[,2]; R5P = out[,3]; G3P = out[,4];
DHCP = out[,5]; PEP = out[,6];
# Elaboração de gráficos verticais
par(mfrow=c(1,5))
plot(t,G6P,type="l")
plot(t,R5P,type="l")
plot(t,G3P,type="l")
plot(t,DHCP,type="l")
plot(t,PEP,type="l")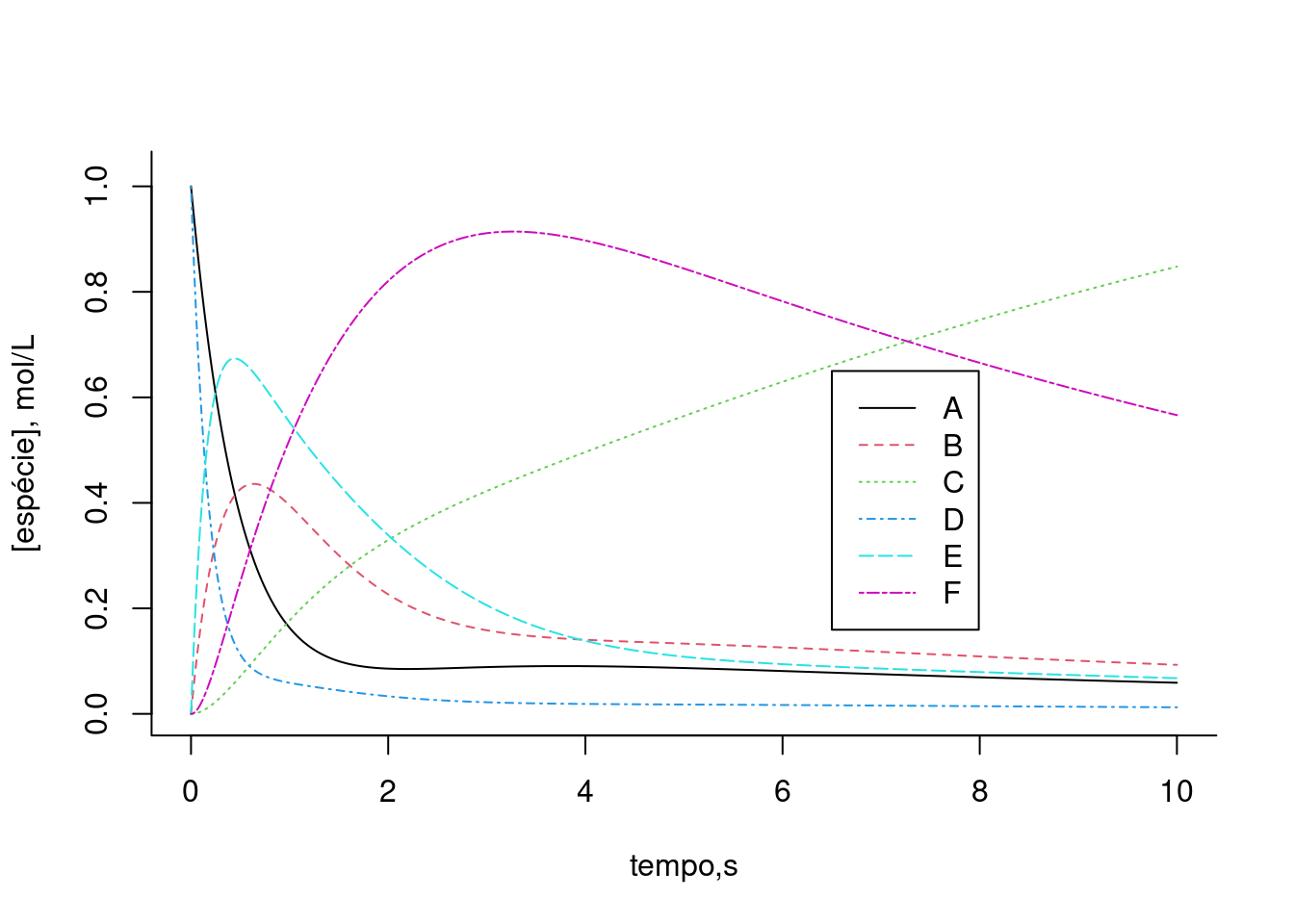
Figura 10.10: Cinética de conversões para uma rede metabólica simples envolvendo algumas reações da glicólise, gliconeogênese e via das pentoses. Valores das constantes cinéticas: k1 = 0,1; k2 = 0,5; k3 = 0,05; k4 = 0,5; k5 = 0,2. Valores iniciais dos compostos: G6P = 1; para os demais, 0.
# Elaboração de gráfico com todas as espécies
par(mfrow=c(1,1))
plot(t,G6P,type="l",col=1,lty=1,ylab="[espécie]",ylim=c(0,1))
lines(t,R5P,type="l",col=2,lty=2)
lines(t,G3P,type="l",col=3,lty=3)
lines(t,DHCP,type="l",col=4,lty=4)
lines(t,PEP,type="l",col=5,lty=5)
legend(x=10,y=1,legend=c("G6P","R5P","G3P","DHCP","PEP"),col=c(1,2,3,4,5),cex=1,lty=c(1,2,3,4,5))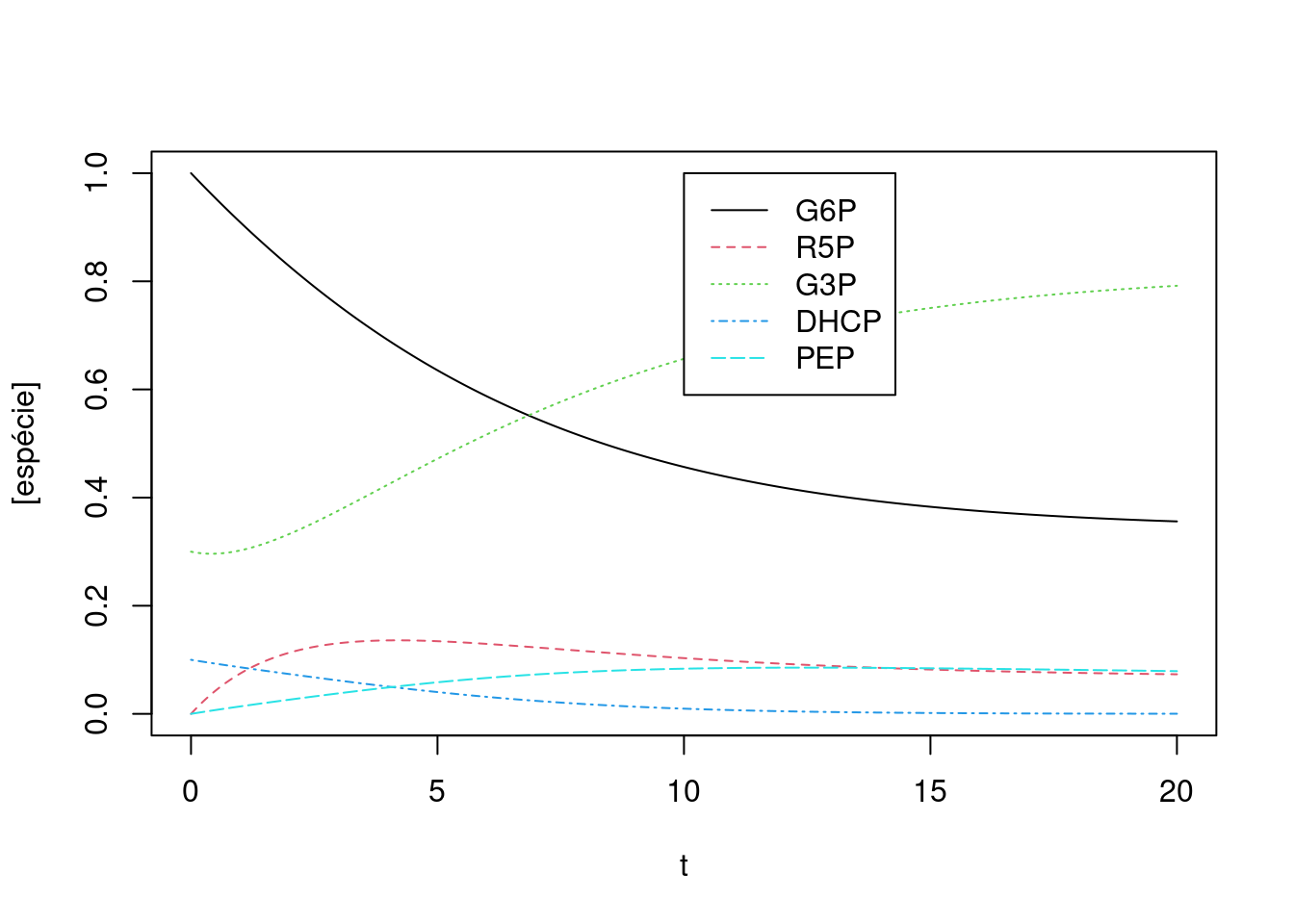
Figura 10.11: Cinética de conversões para uma rede metabólica simples envolvendo algumas reações da glicólise, gliconeogênese e via das pentoses. Valores das constantes cinéticas: k1 = 0,1; k2 = 0,5; k3 = 0,05; k4 = 0,5; k5 = 0,2. Valores iniciais dos compostos: G6P = 1; para os demais, 0.
10.3 Cinética do metabolismo de 6-mercaptopurina

Figura 10.12: Metabolismo esquemático simplificado para o metabolismo de 6-mercaptopurina (adaptado de Lavrova et al., 2017).
lsoda: library(deSolve)
# Parâmetros
k0=5;k1=10;k2=10;k3=5;k4=1e-5;k7=0.01;k8=0.5;km7=1;km1=0.01;km2=4;km3=0.01;km4=0.1;km8=0.01;VPUR=0.01;VD=0.9;VOUT=1e-4
# Lista de parâmetros
parms = c(k0,k1,k2,k3,k4,k7,k8,km7,km1,km2,km3,km4,km8,VPUR,VD,VOUT)
# especificação dos compostos
MPex=x[1]
MPin=x[2]
TIMP=x[3]
TXMP=x[4]
TGMP=x[5]
meTGMP=x[6]
TITP=x[7]
ATP=x[8]
AMP=x[9]
PP=x[10]
# Concentrações iniciais das espécies
reag0=c(MPex0=0.68,MPin0=0,TIMP0=0,TXMP0=0,TGMP0=0,meTGMP0=0,TITP0=0,ATP0=0.2,AMP0=0,PP0=0)
# Definição do intervalo de tempo
tmin = 0; tmax = 2; dt = 0.01
tempo = seq(tmin, tmax, dt)
# Função para as derivadas de cada espécie
eq.dif = function(tempo, x, parms) {
# Definição de parâmetros
MPex=x[1]
MPin=x[2]
TIMP=x[3]
TXMP=x[4]
TGMP=x[5]
meTGMP=x[6]
TITP=x[7]
ATP=x[8]
AMP=x[9]
PP=x[10]
# Equações diferenciais
dMPex = -k0*MPex
dMPin = -(VPUR + k1)*MPin + k0*MPex + km1*TIMP
dTIMP = k1*MPin + km8*TITP - (k2 + k7*ATP + km1 + k8*PP)*TIMP+km2*TXMP + km7*TITP*AMP
dTXMP = k2*TIMP - k3*TXMP*ATP - km2*TXMP + km3*TGMP*AMP* PP
dTGMP = k3*TXMP*ATP - (k4 + VD)*TGMP - km3*TGMP*AMP*PP + km4*meTGMP
dmeTGMP = k4*TGMP - VOUT*meTGMP - km4*meTGMP
dTITP = k8*TIMP*PP - km8*TITP + k7*TIMP*ATP - km7*TITP*AMP
dATP = -k7*TIMP*ATP + km3*TGMP*AMP*PP - k3*TXMP*ATP + km7*TITP*AMP
dAMP = -km3*TGMP*AMP*PP + k3*TXMP*ATP + k7*TIMP*ATP - km7*TITP*AMP
dPP = -k8*TIMP*PP + km8*TITP - km3*TGMP*AMP*PP + k3*TXMP*ATP
list(c(dMPex,dMPin,dTIMP,dTXMP,dTGMP,dmeTGMP,dTITP,dATP,dAMP,dPP)) # lista de valores diferenciais para cada espécie
}
# Rotina de lsoda pra solução equações diferenc. ordinárias
sol.eq = lsoda(reag0,tempo,eq.dif, parms,
rtol=1e-4, atol= 1e-6)
# Isolamento das colunas de resultdos
t = sol.eq[,1]; MPex = sol.eq[,2]; MPin = sol.eq[,3]; TIMP = sol.eq[,4];
TXMP = sol.eq[,5]; TGMP = sol.eq[,6];meTGMP = sol.eq[,7];TITP = sol.eq[,8];ATP = sol.eq[,9];AMP = sol.eq[,10];PP = sol.eq[,11]
# Elaboração do gráfico
plot(t,MPex,type="l",xlab="tempo, dias",ylab="[espécie], umol/L")
lines(t,MPin,type="l",col=2,lty=2)
lines(t,TIMP,type="l",col=3,lty=3)
lines(t,TXMP,type="l",col=4,lty=4)
lines(t,TGMP,type="l",col=5,lty=5)
lines(t,meTGMP,type="l",col=6,lty=6)
lines(t,TITP,type="l",col=7,lty=7)
lines(t,ATP,type="l",col=8,lty=8)
lines(t,AMP,type="l",col=9,lty=9)
lines(t,PP,type="l",col=10,lty=10)
legend(x=1.5,y=0.65,legend=c("MPex","MPin","TIMP","TXMP","TGMP","meTGMP","TITP","ATP","AMP","PP"),col=c(1,2,3,4,5,6,7,8,9,10),cex=0.7,lty=c(1,2,3,4,5,6,7,8,9,10))
Figura 10.13: Dependência da dinâmica da rede metabólica de degradação de 6-mercaptopurina em função do teor inicial de ATP a 0,2 umol/L. Os valores iniciais e parâmetros são descritos no trecho de código.
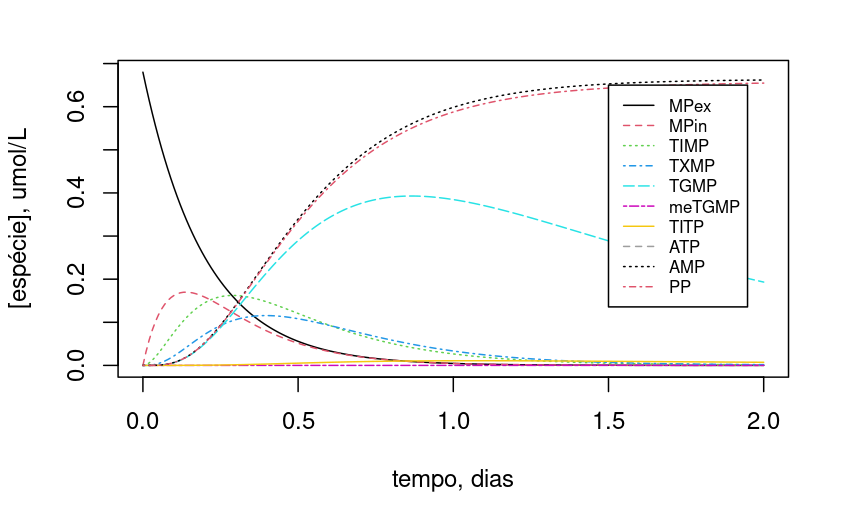
Figura 10.14: Dependência da dinâmica da rede metabólica de degradação de 6-mercaptopurina em função do teor inicial de ATP a 2 umol/L. Os valores iniciais e parâmetros são descritos no trecho de código.