Capítulo 6 Interação Bimolecular

      Quando se menciona interação entre biomoléculas, normalmente se faz referência à processos adsortivos envolvendo um biopolímero (proteína, ácido nucleico, glicano), e um ligante de baixo peso molecular, embora o formalismo também se aplique com alguma restrição a interações entre biopolímeros, e mesmo células inteiras.
      O formalismo mais comum para interação biomolecular é o que envolve a formação de complexo adsortivo entre uma proteína e um ligante (ligand binding), exemplificado para íons (Ca${}^{2+}$, Mg${}^{2+}$, etc), fármacos e candidatos, produtos naturais, e antígenos, dentre vários.
      Perguntas simples acerca da interação ligante-proteína podem elucidar diversas características da formação de tais complexos, como:

1. Quanto de proteína/ligante estão presentes ?
2. Quanto do complexo é formado ?
3. Quão rápido o complexo associa/dissocia ?
4. Quais os mecanismos envolvidos ?

      De modo geral, pode-se representar a interação ligante-proteína como segue:

$$\begin{array}{}P+L\begin{array}{c}{}_{k_{on}}\\ \rightleftharpoons \\ {}^{k_{off}}\end{array}PL& \text{(6.1)}\end{array}$$

Onde P representa o teor de proteína livre, L o ligante livre, e PL o complexo formado. As taxas de reação são definidas para a formação (k${}_{on}$; M${}^{-1}$s${}^{-1}$) e dissociação (k${}_{off}$; s${}^{-1}$) do complexo.

      Dessa forma deduz-se a equação para a isoterma de interação do ligante com a proteína como segue:

$$\begin{array}{}Kd=\frac{\left[P\right]\ast \left[L\right]}{\left[P\right]+\left[L\right]}& \text{(6.2)}\end{array}$$

Onde Kd representa a constante de equilíbrio de dissociação para o complexo PL formado, tal como condicionado ao equilíbrio de formação/dissociação do complexo (v${}_{assoc}$ = v${}_{dissoc}$), e também definido como:

$$\begin{array}{}Kd=\frac{k_{off}}{k_{on}}& \text{(6.3)}\end{array}$$

      A partir da Eq. (6.2) pode-se facilmente deduzir a expressão final para a interação de um ligante a um conjunto de sítios de mesma afinidade na proteína:

$$\begin{array}{}\nu =\frac{n\ast \left[L\right]}{Kd+\left[L\right]}& \text{(6.4)}\end{array}$$

6.1 Modelos de Interação e Representações Lineares

      Observe que a equação (6.4) praticamente repete o formalismo já visto com a formação do complexo ativado de enzima-substrato (5.2), bem como sua representação resultante como uma hipérbole quadrática. De fato, ocorre essencialmente a substituição do parâmetro cinético v da reação pelo parâmetro termodinâmico $\nu$ (“nu”, do Grego) para a isoterma de ligação. As demais quantidades envolvidas mantém-se análogas (P no lugar de E; L no lugar de S;Kd no lugar de Km; e n no lugar de Vmax).
      Mantida essa similaridade com o formalismo da equação de Michaelis-Menten, da mesma maneira decorrem as linearizações para a Eq. (6.4), bem como ajustes não lineares à mesma, na busca de uma solução analítica para os parâmetros termodinâmicos Kd e n. Exemplificando um trecho de código para as linearizações mais comuns no tratamento de dados de interação ligante-proteína:

L=c(0.1,0.2,0.5,1,5,10,20)*1e-6
Kd=1e-6;n=1
v=n*L/(Kd+L)
par(mfrow=c(2,3)) # estabelece área de plot pra 6 gráficos
plot(L,v,type="o",main="Direto")
plot(log(L),v,type="o",main="Langmuir")
plot(1/L,1/v,type="o",main="Klotz")
plot(v,v/L,type="o",main="Scatchard")
plot(L,L/v,type="o",main="Woolf")
plot(log10(L),log10(v/(n-v)),type="o",main="Hill")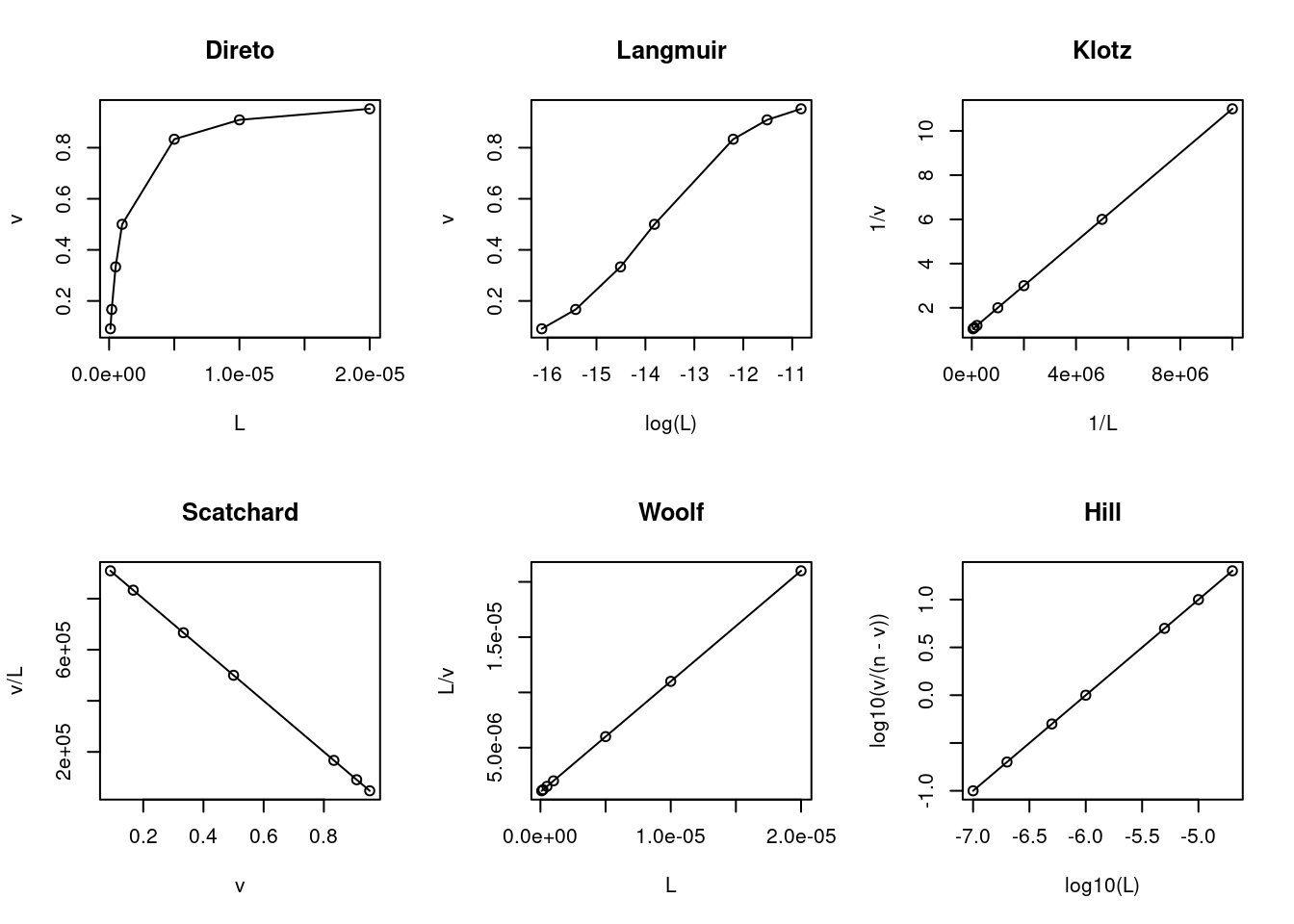 

Figura 6.1: Principais linearizações da isoterma de ligação ligante-proteína.

par(mfrow=c(1,1)) # volta à janela gráfica normal

      Desvios da linearidade, por outro lado, são frequentemente utilizados como diagnósticos para modelos que distintos do de homogeneidade de sítios de ligação como acima (heterogeneidade de sítios, criação de sítio, cooperatividade. As equações abaixo descrevem esses modelos, e consideram K, constante de equilíbrio de associação ligante-proteína, como o reverso de Kd, a fim de tornar as expressões mais legíveis:

$$\begin{array}{}K=\frac{1}{Kd}& \text{(6.5)}\end{array}$$

      O modelo de heterogeneidade de sítios de ligação pressupõe que haja na proteína mais um sítio com afinidades distintas para o ligante ((Dahlquist 1978)). Formalmente esse modelo pode ser exemplificado para 2 conjuntos de sítios de ligação, como segue:

$$\begin{array}{}\nu =\frac{K1\ast \left[L\right]}{1+K1\ast \left[L\right]}+\frac{K2\ast \left[L\right]}{1+K2\ast \left[L\right]}& \text{(6.6)}\end{array}$$

      O trecho de código abaixo exemplifica o modelo no ‘R’, bem como suas principais linearizações diagnósticas.

L=c(0.1,0.2,0.5,1,5,10,20)*1e-6
Kd1=2e-6;n1=1;
Kd2=2e-8;n2=1
v=(n1*L/(Kd1+L))+(n2*L/(Kd2+L))

par(mfrow=c(2,3)) # estabelece área de plot pra 6 gráficos
plot(L,v,type="o",main="Direto")
plot(log(L),v,type="o",main="Langmuir")
plot(1/L,1/v,type="o",main="Klotz")
plot(v,v/L,type="o",main="Scatchard")
plot(L,L/v,type="o",main="Woolf")
plot(log10(L),log10(v/(n1+n2-v)),type="o",main="Hill") # n1+n2=ntot no Hill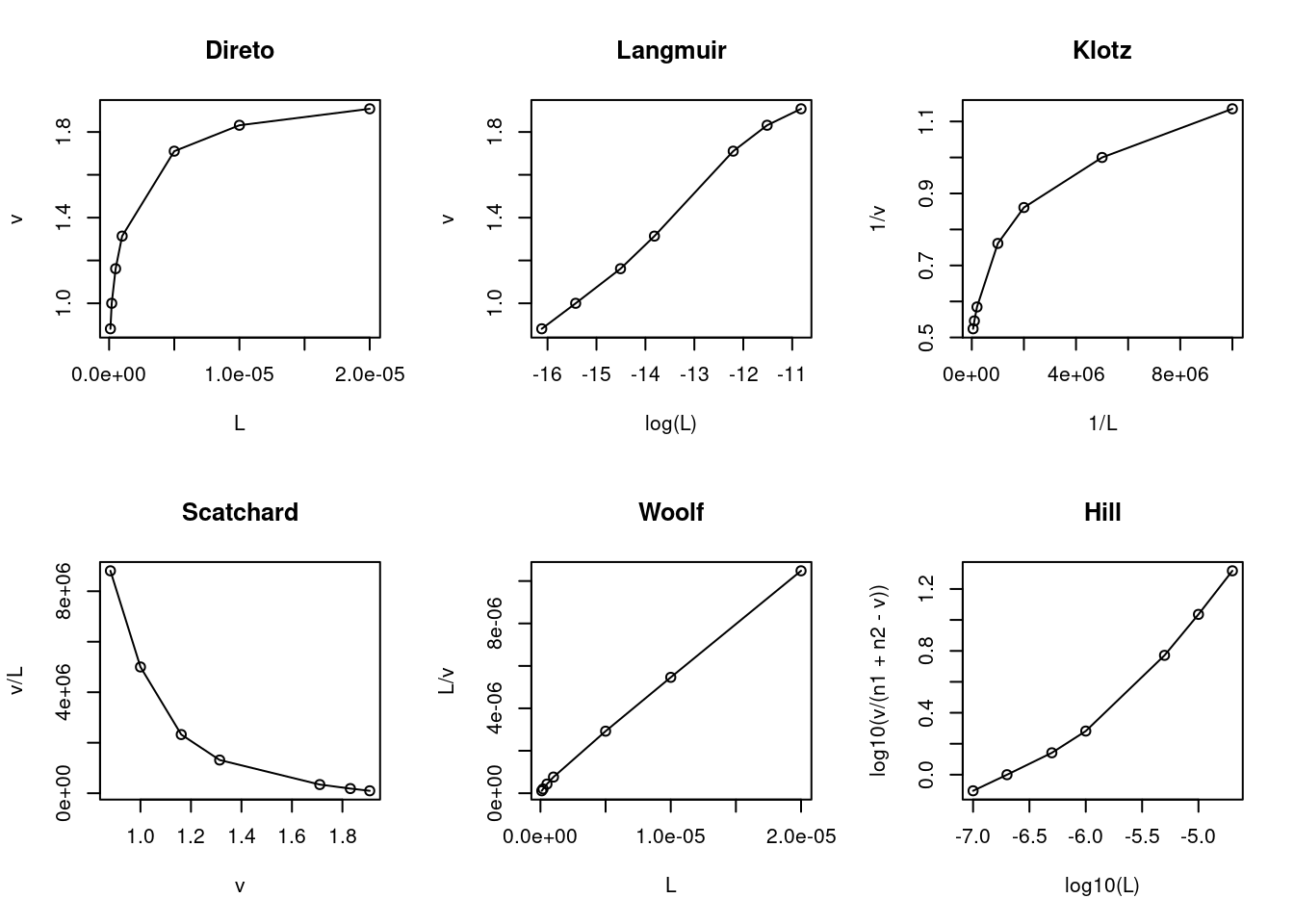

Figura 6.2: Modelo e linearizações para heterogeneidade de 2 conjuntos de sítios de ligação

par(mfrow=c(1,1)) # volta à janela gráfica normal

      O modelo de criação de novo sítio - “one-site creator”; (Parsons and Vallner 1978) estabelece uma cooperatividade positiva resultante da produção de novos sítios para o ligante na proteína. Segue o modelo exemplificado e suas linearizações resultantes.

L=c(0.1,0.2,0.5,1,5,10,20)*1e-6
Kd1=2e-6;n1=1
Kd2=2e-5;n2=1
nH=0.5
v=(n1*L*1/Kd1)/(1+1/Kd1*L)+((n2*1/Kd1*1/Kd2*L^2)/(1+1/Kd1*L)*(1+1/Kd2*L))
par(mfrow=c(2,3)) # estabelece área de plot pra 6 gráficos
plot(L,v,type="o",main="Direto")
plot(log(L),v,type="o",main="Langmuir")
plot(1/L,1/v,type="o",main="Klotz")
plot(v,v/L,type="o",main="Scatchard")
plot(L,L/v,type="o",main="Woolf")
plot(log10(L),log10(v/(n-v)),type="o",main="Hill") # n1+n2=ntot no Hill

## Warning in xy.coords(x, y, xlabel, ylabel, log): NaNs produced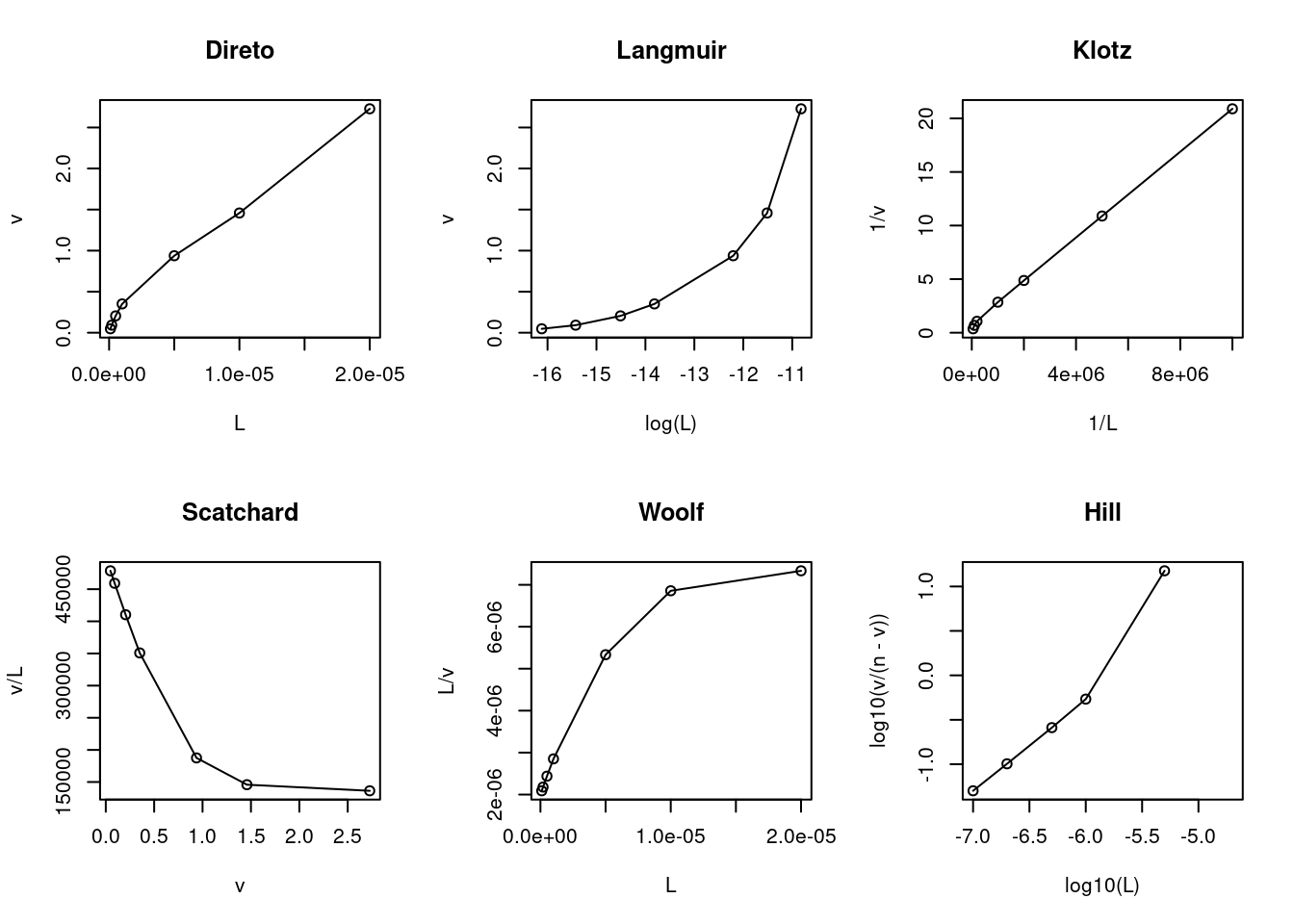

Figura 6.3: Modelo e linearizações para criação de novo sítio: 1-site creator.

par(mfrow=c(1,1)) # volta à janela gráfica normal

      Os modelos de cooperatividade (negativa e positiva) seguem um formalismo similar descrito para a ligação de oxigênio à hemoglobina junto ao capítulo 4 (Eq. (4.2)). Na cooperatividade negativa uma segunda molécula de ligante interage com a proteína com menor afinidade:

L=c(0.1,0.2,0.5,1,5,10,20)*1e-6
Kd=2e-6;n=1
nH=0.5
v=(n*L^nH/(Kd+L^nH))
par(mfrow=c(2,3)) # estabelece área de plot pra 6 gráficos
plot(L,v,type="o",main="Direto")
plot(log(L),v,type="o",main="Langmuir")
plot(1/L,1/v,type="o",main="Klotz")
plot(v,v/L,type="o",main="Scatchard")
plot(L,L/v,type="o",main="Woolf")
plot(log10(L),log10(v/(n-v)),type="o",main="Hill") # n1+n2=ntot no Hill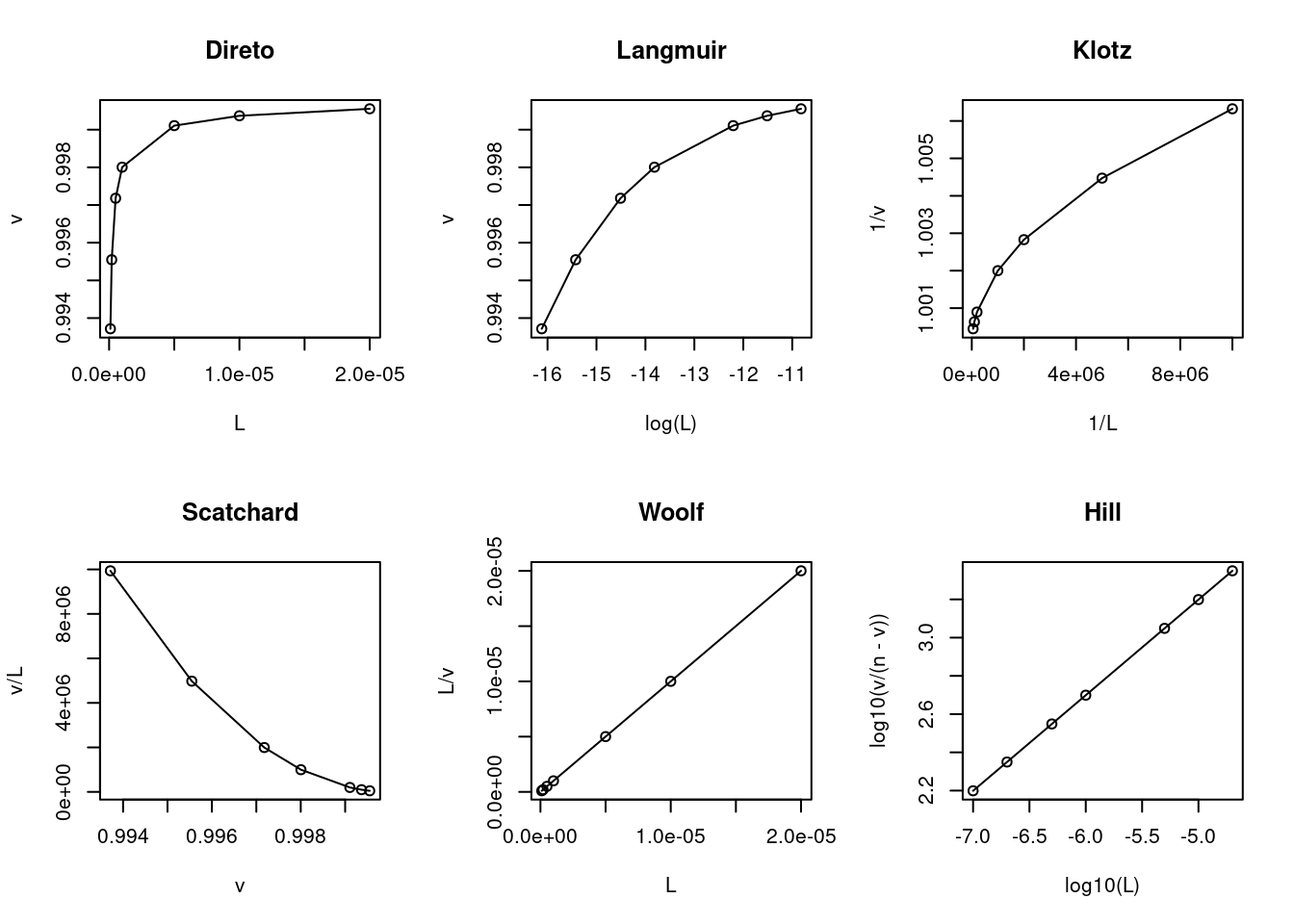

Figura 6.4: Modelo e linearizações para cooperatividade negativa de sítios de ligação.

par(mfrow=c(1,1)) # volta à janela gráfica normal

      Já na cooperatividade positiva, uma segunda molécula de ligante interage com a proteína com maior afinidade que a primeira molécula (Parsons and Vallner 1978):

L=c(0.1,0.2,0.5,1,5,10,20)*1e-6
Kd=2e-6;n=1
nH=1.5
v=(n*L^nH/(Kd+L^nH))
par(mfrow=c(2,3)) # estabelece área de plot pra 6 gráficos
plot(L,v,type="o",main="Direto")
plot(log(L),v,type="o",main="Langmuir")
plot(1/L,1/v,type="o",main="Klotz")
plot(v,v/L,type="o",main="Scatchard")
plot(L,L/v,type="o",main="Woolf")
plot(log10(L),log10(v/(n-v)),type="o",main="Hill") # n1+n2=ntot no Hill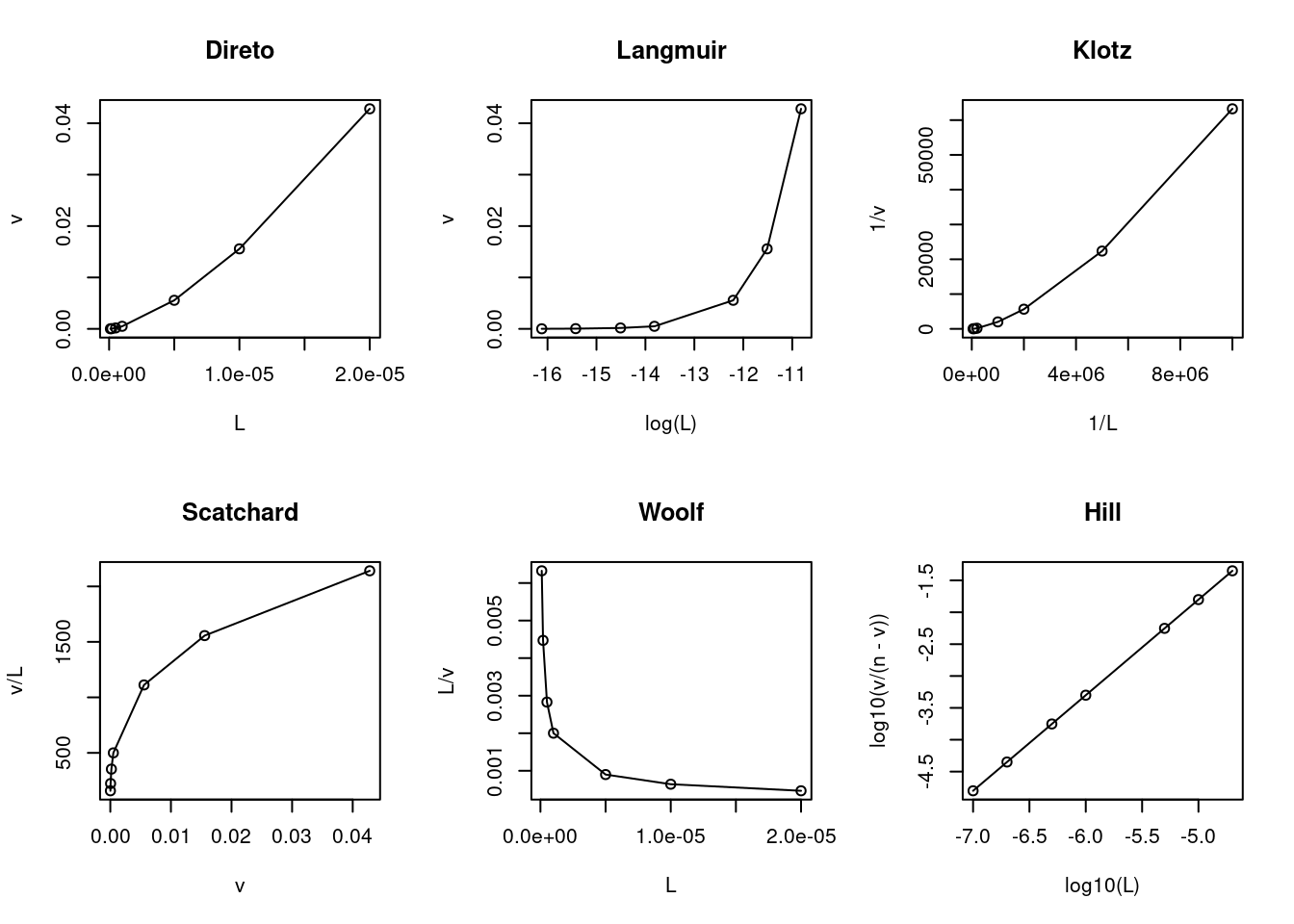

Figura 6.5: Modelo e linearizações para cooperatividade positiva de sítios de ligação.

par(mfrow=c(1,1)) # volta à janela gráfica normal

      Observe que a inclinação do gráfico de Hill é inferior à unidade para a cooperatividade negativa, e superior a essa, para a cooperatividade positiva, e representa o mesmo parâmetro nH visto na Eq.(4.2).
      Ainda que sujeito à crítica por sua inconsistência estatística (variável dependente em ambos os eixos), a representação de Scatchard tem sido privilegiada ao longo de décadas como diagnóstico de modelos de interação ligante-proteína. Entre suas vantagens, aloca-se a possibilidade de facilmente distinguir-se o modelo de cooperatividade positiva (aclive) do de heterogeneidade de sítios de ligação (declive abrupto) ou de cooperatividade negativa (declive suave).

6.2 Ajuste Não-Linear Em Interação Ligante-Proteína

      Ajustes diretos da equação não linear dos modelos de interação também podem ser efetuados como fora realizado para a equação de Michaelis-Menten no capítulo 5 sobre Enzimas. Exemplificando, pode-se simular a obtenção de dados experimentais de binding pelo trecho a seguir, utilizando-se o comando ‘runif’ (random uniform) para geração de sequência aleatória (como fora realizado no capítulo 5.

# Isoterma de Interação Ligante-Proteína
n=1
Kd=10
L=120
i=3
L=seq(0, L, i)
v=(L*n)/(Kd+L)+rnorm(40,0,0.1)

## Warning in (L * n)/(Kd + L) + rnorm(40, 0, 0.1): longer object length is not a
## multiple of shorter object length

plot(L,v)

      Observe que o comando ‘rnorm’ adiciona um erro de distribuição normal aos dados. Outra forma para simulação desses é dada abaixo, introduzindo-se o comando ‘runif’ de geração de números aleatórios.

# Simulação de dados de interação bimolecular (1 sítio)

# Simulação de dados
set.seed(20160227) # estabelece semente para geração de números aleatórios
L<-seq(0,50,1)
PL<-((runif(1,10,20)*L)/(runif(1,0,10)+L))+rnorm(51,0,1) 
# 1. runif(n,min,max); quando sem atributos, considera-se min=0  e max=1
# 2. rnorm(no. pontos,media,desvio) - erro aleatório de distribuição normal
plot(L,PL, xlab="L", ylab="PL")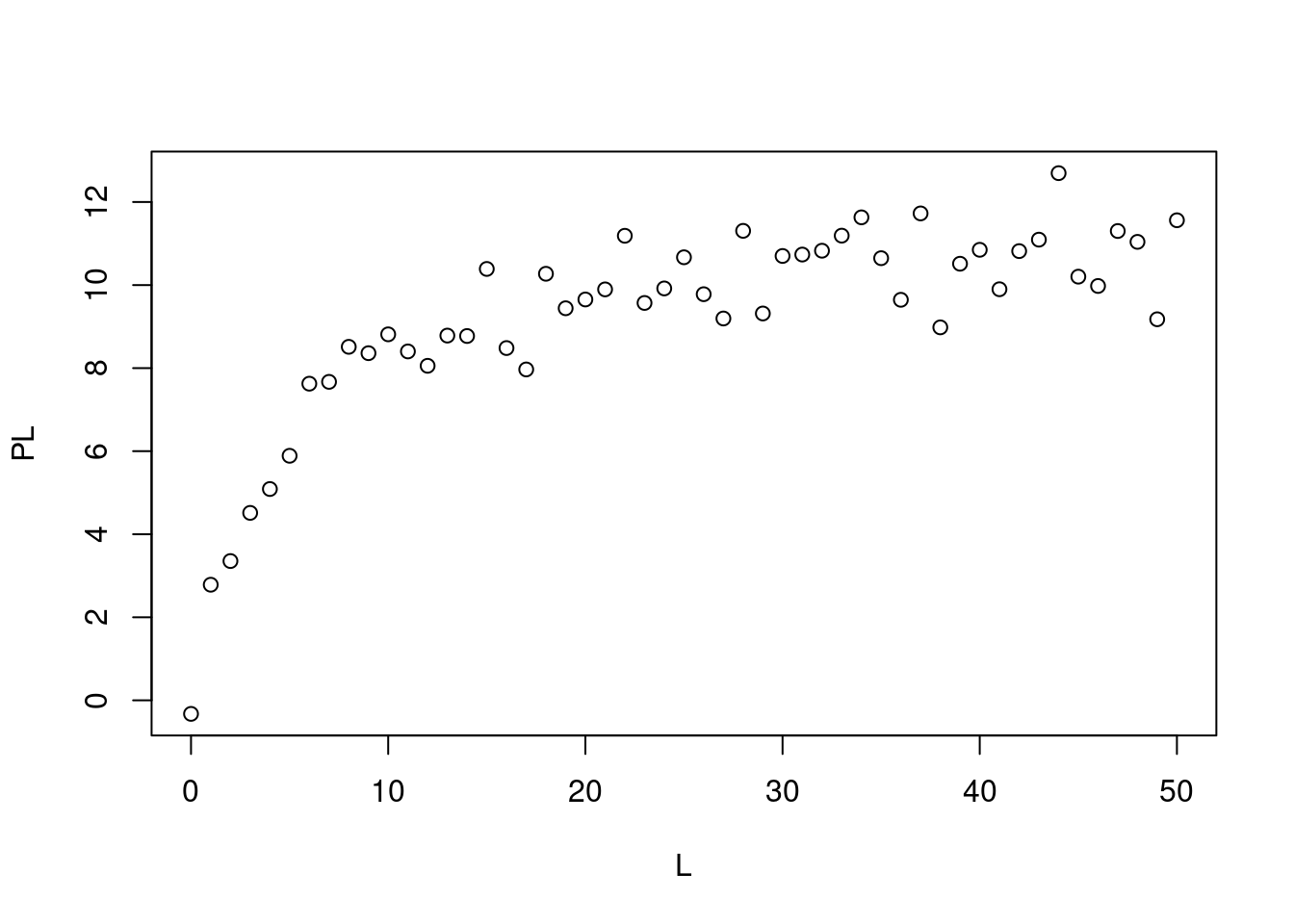

Figura 6.6: Dados simulados para isoterma de interação bimolecular.

      Agora precisamos utilizar o comando ‘nls’ para o ajuste não linear, sobreposição da curva teórica, e tabela estatística de resultados:

#Ajuste não linear
m<-nls(PL~n*L/(Kd+L),start=list(n=1,Kd=1))

#Coef. de correlação
cor(PL,predict(m)) # Coeficiente de correlação de Pearson

## [1] 0.9

#Gráfico de dados e simulação
plot(L,PL)
lines(L,predict(m),lty=2,col="red",lwd=3)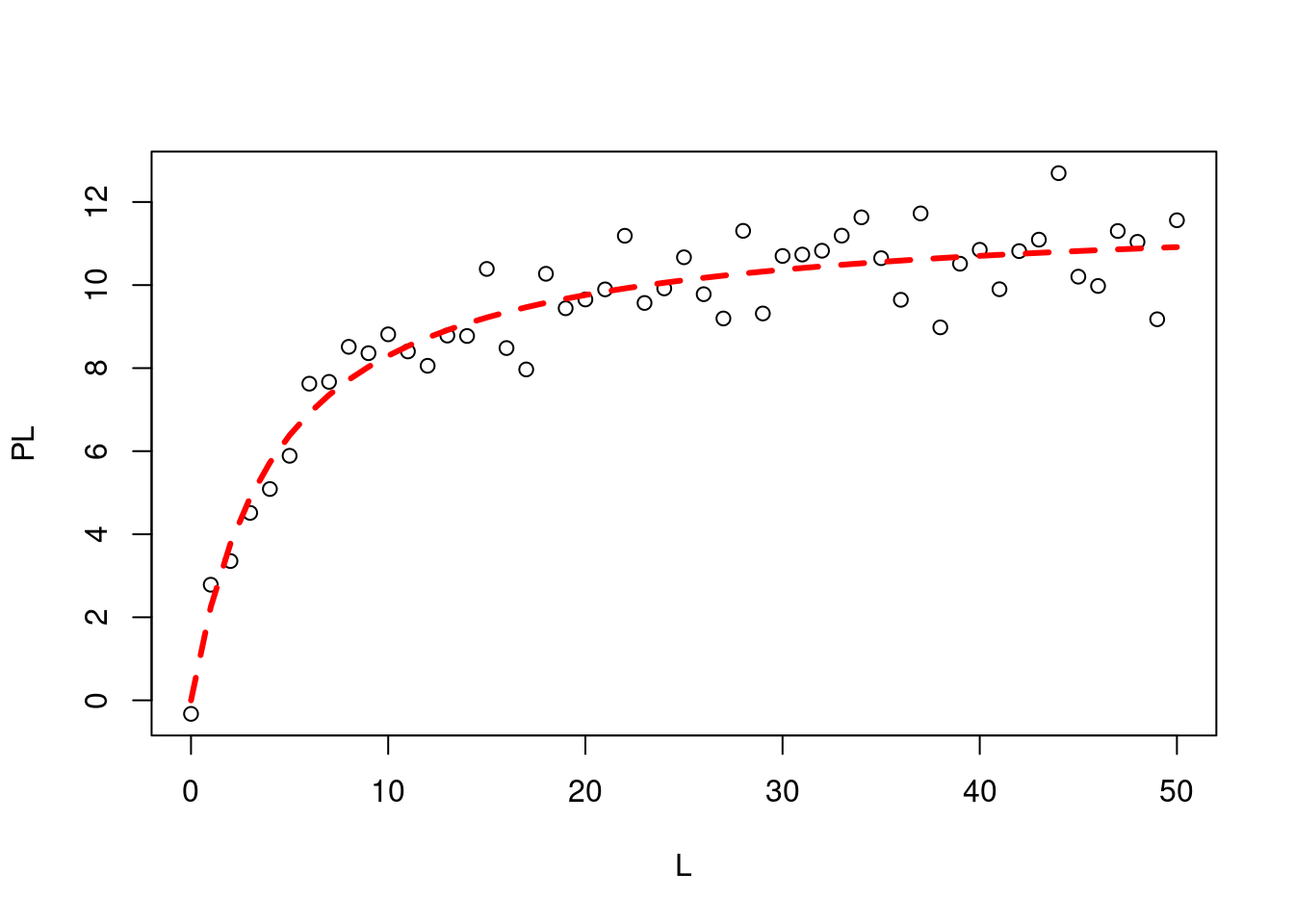

summary(m)

## 
## Formula: PL ~ n * L/(Kd + L)
## 
## Parameters:
##    Estimate Std. Error t value Pr(>|t|)    
## n    11.848      0.262   45.22  < 2e-16 ***
## Kd    4.278      0.511    8.37  5.3e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8 on 49 degrees of freedom
## 
## Number of iterations to convergence: 6 
## Achieved convergence tolerance: 1.55e-06

6.3 Sistemas Gráficos no R

      A última curva de simulação obtida o foi junto à biblioteca padrão para manipulação de gráficos da instalação do ‘R’, Graphics. Trata-se um conjunto de funções amplo também utilizado por vários outros pacotes do ambiente. Contudo, existem no ‘R’ diversas outras bibliotecas para elaboração de gráficos, dentre os quais vale destacar o Lattice, também incluido na instalação padrão, e o ggplot2. Ambos os sistemas geram resultados com melhor estética e flexibilidade gráfica que a biblioteca Graphics padrão, e possuem empregos e semânticas distintas entre si.
      O sistema Lattice (Sarkar 2008) é baseado no sistema Trellis para representação gráfica de dados multivariados. Sua força está na representação de dados em paineis contendo subgrupos e, embora tenha sintaxe menos intuitiva e por vezes mais elaborada que o pacote Graphics, produz um grafismo superior a esse com poucos cliques de teclado. De modo geral, o Lattice produz o gráfico dentro do próprio algoritmo, de modo diferente aos sistemas Graphics (pode-se acumular linhas sucessivas de modificação do gráfico) ou ggplot2.
     Por outro lado a biblioteca ggplot2 é baseada na gramática de gráficos (Wickham 2011), e produz o gráfico utilizando uma única linha de comando que combina camadas sobrepostas, de modo similar à aplicativos de manipulação de imagens (ex: Inkscape, Gimp, Corel Draw, Photoshop). Dessa forma é possível alterar cada ítem do gráfico em suas camadas específicas (tema, coordenadas, facets, estatísticas, geometria, estética, dados). Exemplificando o resultado gráfico da curva de simulação acima de binding para Lattice e ggplot2:

# Simulação de dados
set.seed(20160227) # estabelece semente para geração de números aleatórios
L<-seq(0,50,1)
PL<-((runif(1,10,20)*L)/(runif(1,0,10)+L))+rnorm(51,0,1) 
# 1. runif(n,min,max); quando sem atributos, considera-se min=0  e max=1
# 2. rnorm(no. pontos,media,desvio) - erro aleatório de distribuição normal

# Produção do gráfico com sistema Lattice
library(lattice)
xyplot(PL~L)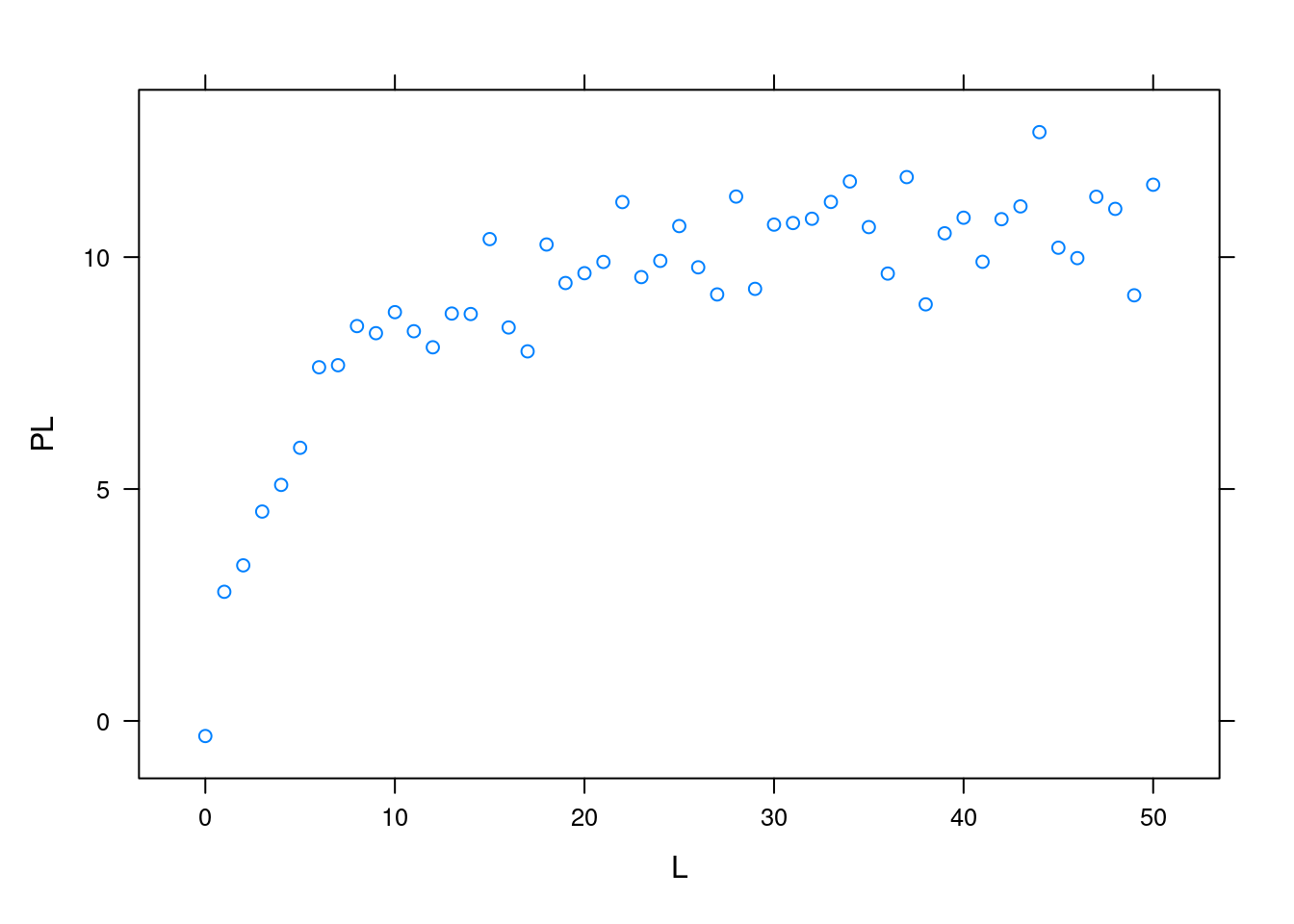

# Produção do gráfico com sistema ggplot2
library(ggplot2)
qplot(L,PL)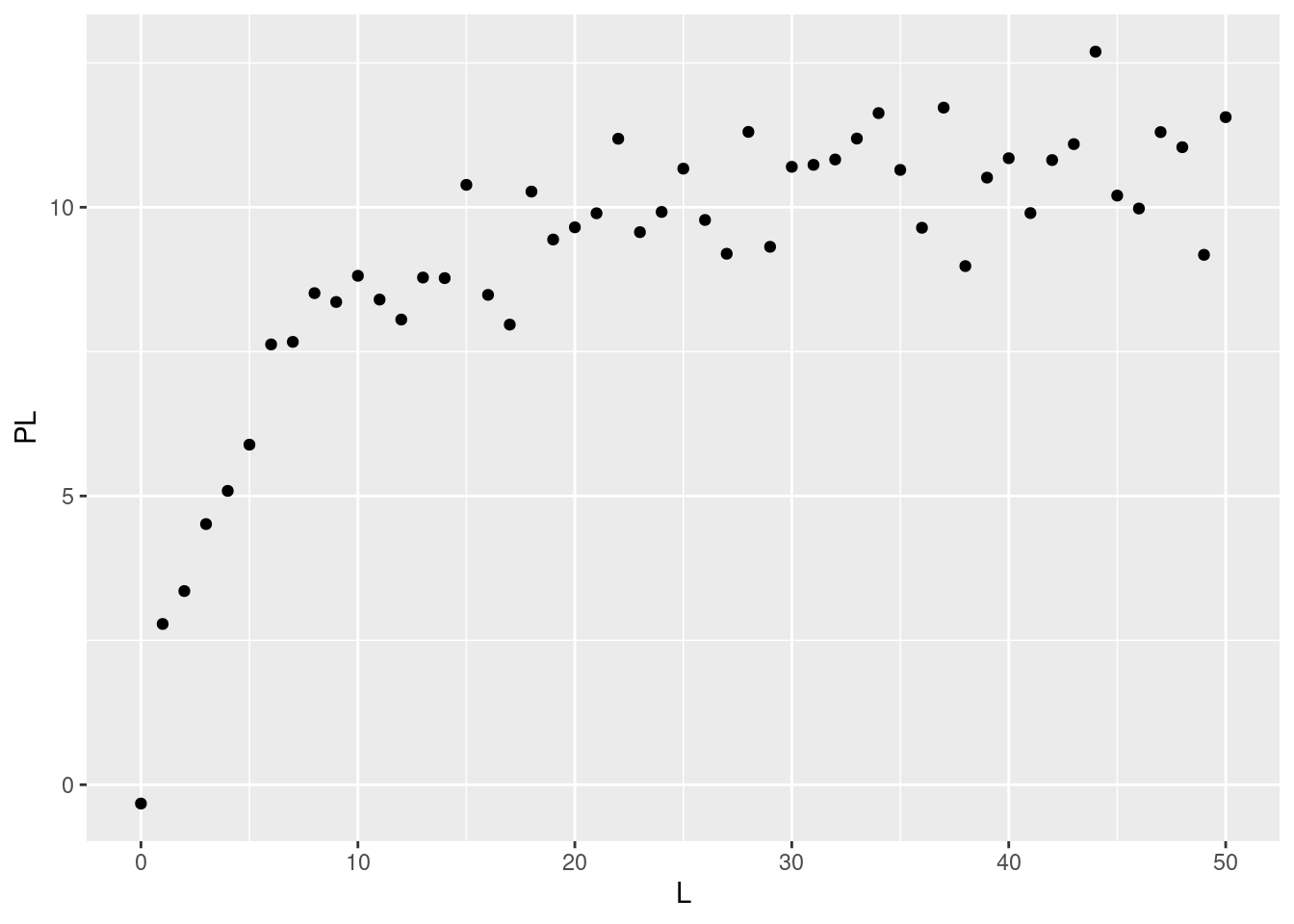

      Como a percepção de peculiaridades dos sistemas gráficos se revela melhor com dados mais elaborados, as ilustrações a seguir utilizarão o conjunto de dados ‘Puromycin’, que integra a biblioteca ‘datasets’ do ‘R’. Os dados apresentam a velocidade de reação enzimática sobre um substrato em células tratadas e não tratadas com puromicina.

      O código abaixo retorna a plotagem, ajuste não linear e resultados obtidos com a biblioteca Graphics padrão, e foi extraído do própria documentação do dataset.

library(datasets)

plot(rate ~ conc, data = Puromycin, las = 1,
     xlab = "[S], mM",
     ylab = "v (contagem/min/min)",
     pch = as.integer(Puromycin$state),
     col = as.integer(Puromycin$state),
     main = "Ilustração de Ajuste Com Graphics")

## Ajuste da equação de Michaelis-Mentem
fm1 <- nls(rate ~ Vm * conc/(K + conc), data = Puromycin,
           subset = state == "treated",
           start = c(Vm = 200, K = 0.05))
fm2 <- nls(rate ~ Vm * conc/(K + conc), data = Puromycin,
           subset = state == "untreated",
           start = c(Vm = 160, K = 0.05))
summary(fm1)

## 
## Formula: rate ~ Vm * conc/(K + conc)
## 
## Parameters:
##    Estimate Std. Error t value Pr(>|t|)    
## Vm 2.13e+02   6.95e+00   30.61  3.2e-11 ***
## K  6.41e-02   8.28e-03    7.74  1.6e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11 on 10 degrees of freedom
## 
## Number of iterations to convergence: 5 
## Achieved convergence tolerance: 8.82e-06

summary(fm2)

## 
## Formula: rate ~ Vm * conc/(K + conc)
## 
## Parameters:
##    Estimate Std. Error t value Pr(>|t|)    
## Vm 1.60e+02   6.48e+00   24.73  1.4e-09 ***
## K  4.77e-02   7.78e-03    6.13  0.00017 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10 on 9 degrees of freedom
## 
## Number of iterations to convergence: 5 
## Achieved convergence tolerance: 4.45e-06

## Adição de linhas de ajuste ao plot
conc <- seq(0, 1.2, length.out = 101)
lines(conc, predict(fm1, list(conc = conc)), lty = 1, col = 1)
lines(conc, predict(fm2, list(conc = conc)), lty = 2, col = 2)
legend(0.8, 120, levels(Puromycin$state),
       col = 1:2, lty = 1:2, pch = 1:2)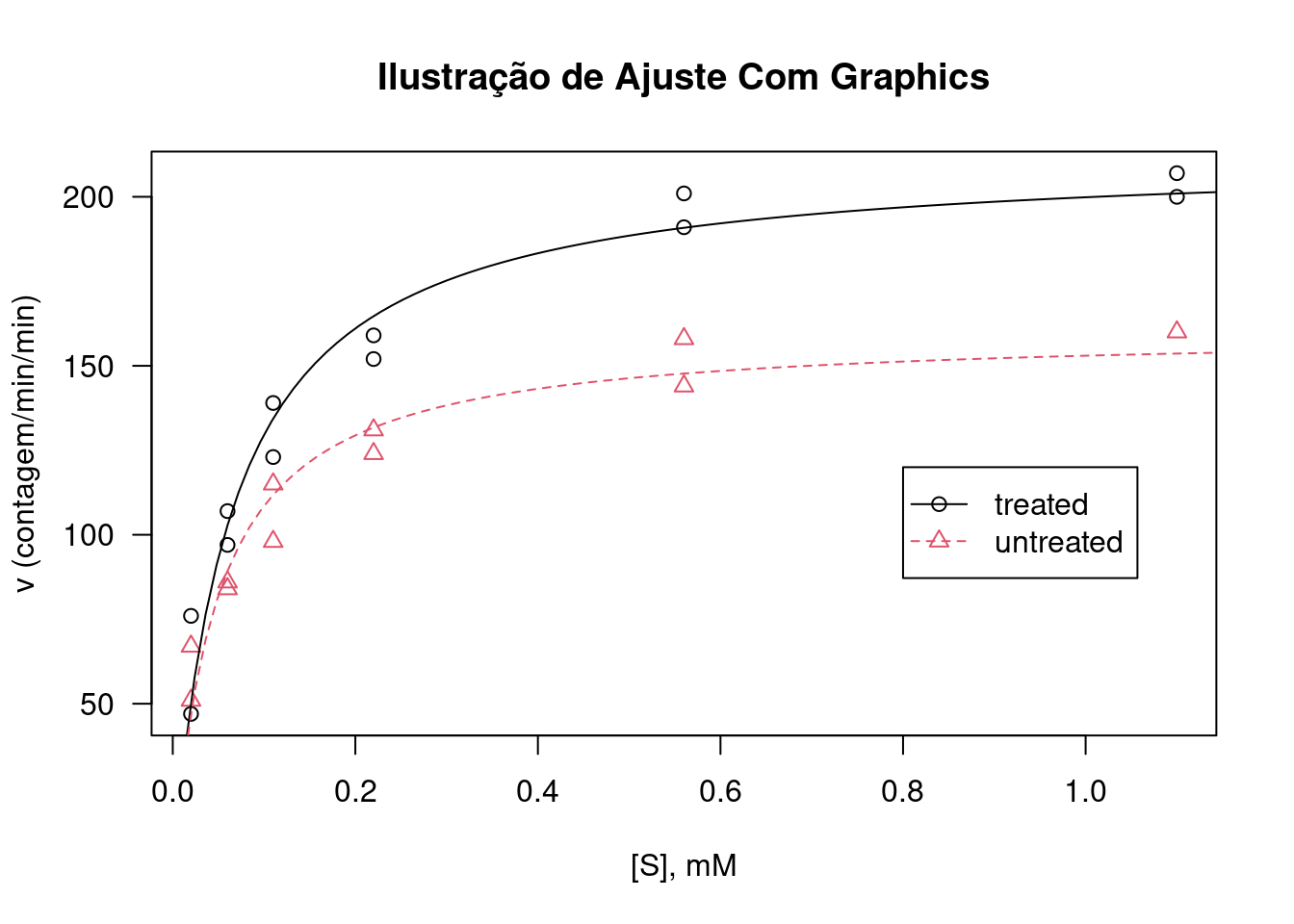

Figura 6.7: Plotagem e análise com graphics.

      O sistema ggplot2, por sua vez, exige que os comandos sejam elencados em camadas justapostas intercaladas com o sinal “+”, como segue:

library(datasets)
p <- ggplot(data=Puromycin, aes(conc, rate, color = state)) +
  geom_point() +
  geom_smooth(
    method       = "nls",
    formula      = y ~ Vm*x/(Km+x),
    method.args  = list(start = list(Vm = 200, Km = 0.1)),
    se           = FALSE 
  ) # expressão que define o plot
p # variável que apresenta o plot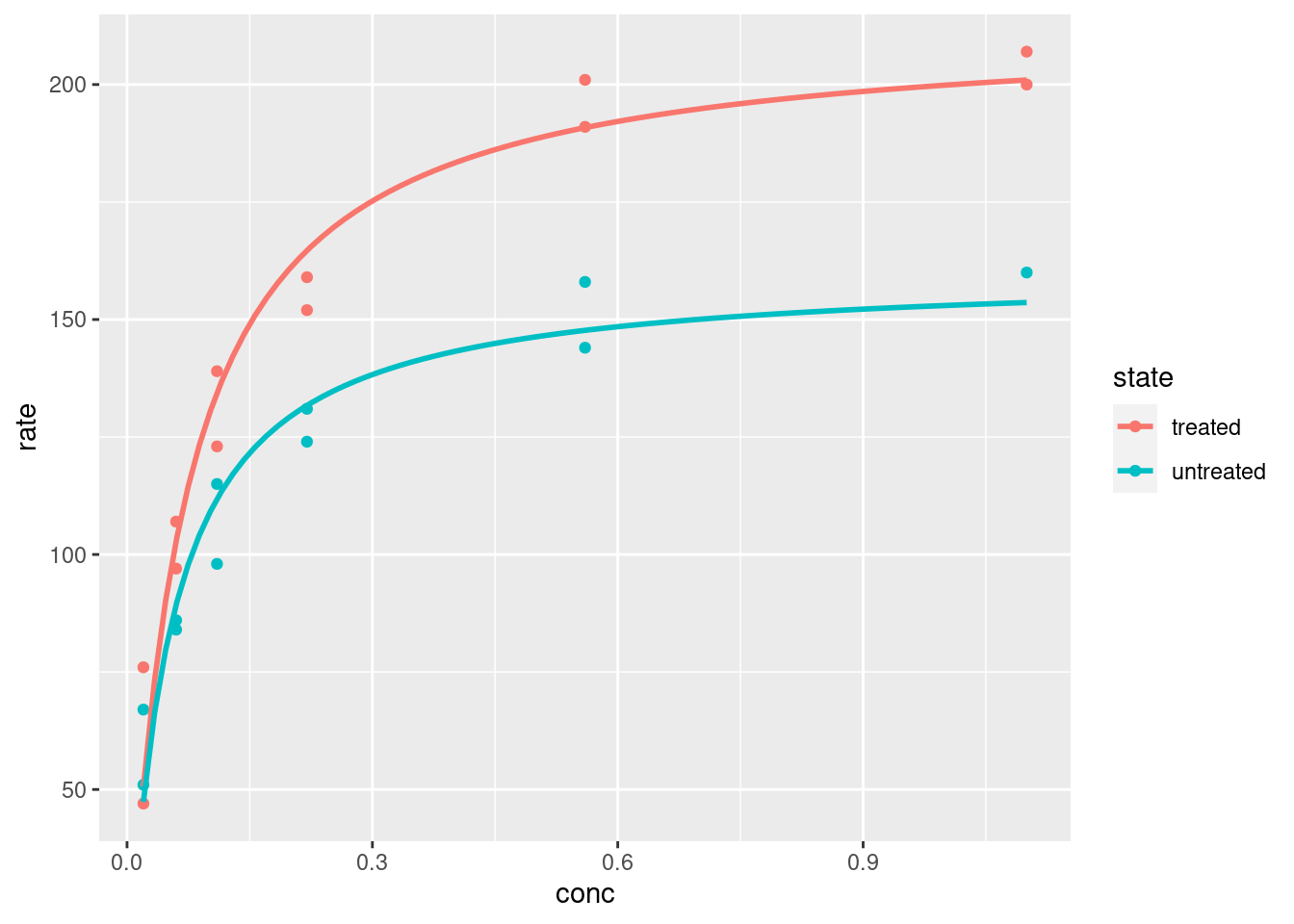

Figura 6.8: Plotagem e análise com ggplot2.

      Perceba o menor número de instruções do script para a produção do gráfico. Além disso, e diferente do Graphics, ggplot2 permite adicionar camadas à linha de comandos principais, e apresentar os dados multivariados em paineis (funções ‘facet_grid’ e ‘facet_wrap’), sem a necessidade de se utilizar o comando ‘mfrow’ ou ‘mfcol’ visto no capítulo, como segue:

p + facet_grid(rows = vars(state))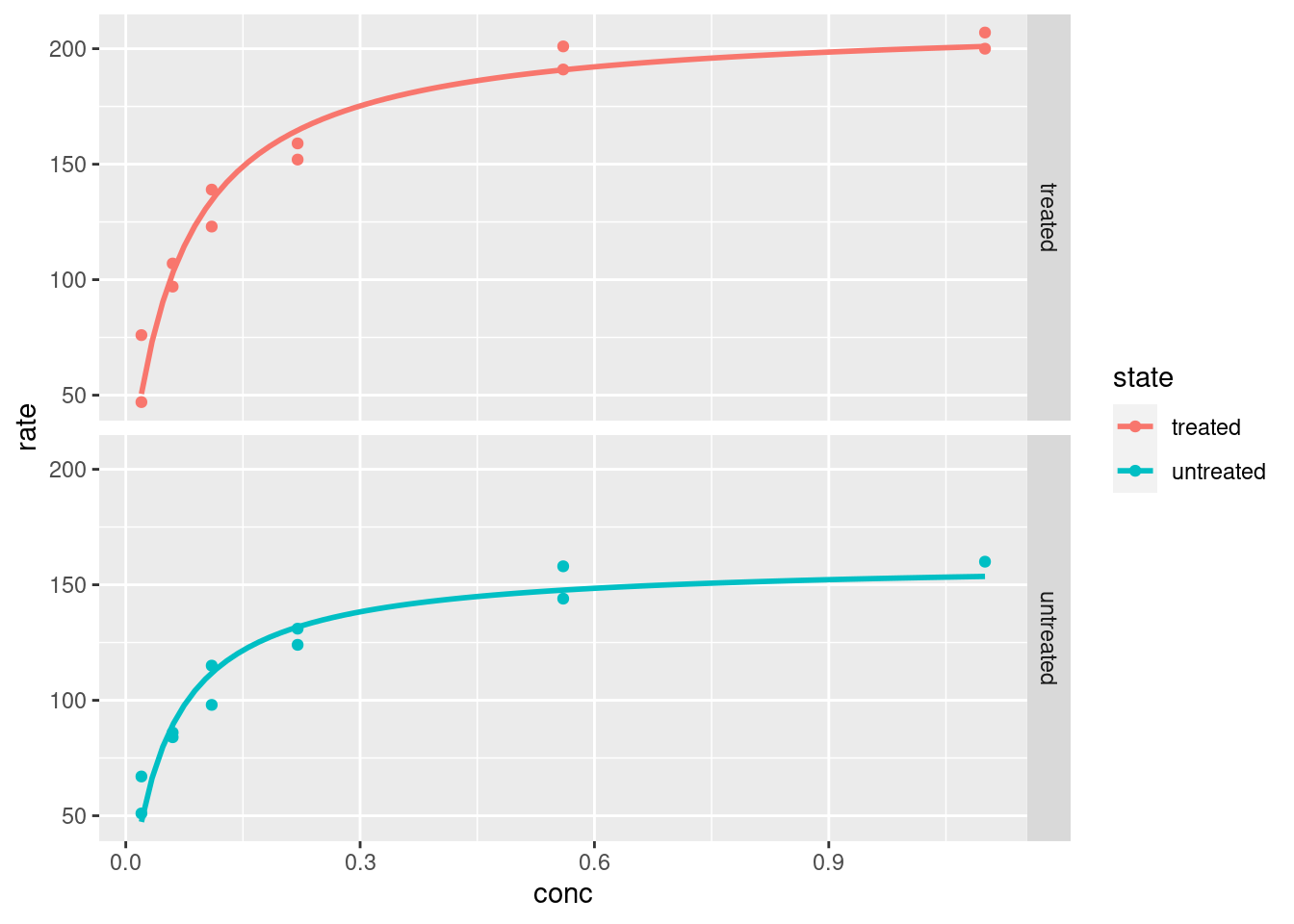

Figura 6.9: Plotagem e análise com ggplot2 - paineis (faceting).

      Lattice também possui uma economia de instruções em relação à Graphics. Não considerando o ajuste estatístico, os grupos podem ser apresentados simplesmente utilizando-se a fórmula:

$$\begin{array}{}xyplot(y\sim x|groups=z)& \text{(6.7)}\end{array}$$

library(lattice)
xyplot(rate ~ conc, data = Puromycin, groups=state)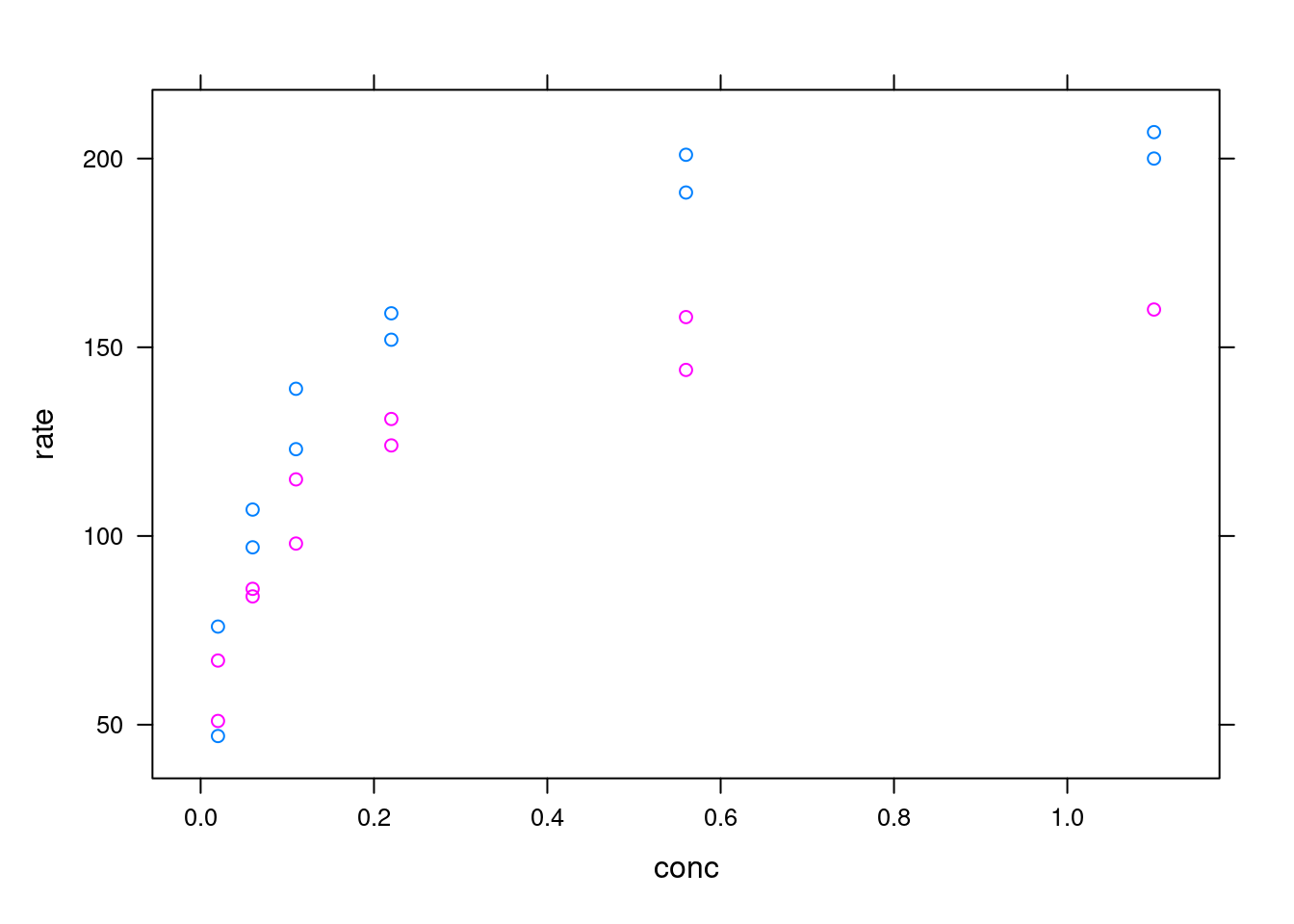

      E para a representação dos ajustes não lineares:

library(nlme)
n1<-nlsList(rate ~ Vmax*conc/(Km+conc) | state, data=Puromycin, start=list(Vmax=200, Km=0.1))
summary(n1)
xyplot(rate ~ conc,groups = state, data =
         Puromycin) +
  layer(panel.curve(Vmax[1]*x/(Km[1]+x),col=1),
        data = as.list(coef(n1))) +
  layer(panel.curve(Vmax[2]*x/(Km[2]+x),col=2),
        data = as.list(coef(n1)))

      A biblioteca Lattice também permite a apresentação em paineis; diferente de ggplot2, contudo, o gráfico é gerado algoritmicamente, sem a sobreposição de comandos:

library(nlme) # pacote quer permite regressão não linear com subgrupos

## 
## Attaching package: 'nlme'

## The following object is masked from 'package:dplyr':
## 
##     collapse

## The following object is masked from 'package:seqinr':
## 
##     gls

nonlinLatt<-nlsList(rate~Vmax*conc/(Km+conc)| state, start=list(Vmax=200, Km=0.1), data=Puromycin)
summary(nonlinLatt)

## Call:
##   Model: rate ~ Vmax * conc/(Km + conc) | state 
##    Data: Puromycin 
## 
## Coefficients:
##    Vmax 
##           Estimate Std. Error t value Pr(>|t|)
## treated        213          7      32    3e-11
## untreated      160          7      23    1e-09
##    Km 
##           Estimate Std. Error t value Pr(>|t|)
## treated       0.06      0.008       8    2e-05
## untreated     0.05      0.008       6    2e-04
## 
## Residual standard error: 10 on 19 degrees of freedom

xyplot(rate + fitted(nonlinLatt)~conc| state, data=Puromycin,
       type=c("p","l"),distribute.type=TRUE,col.line="red",
       ylab="rate")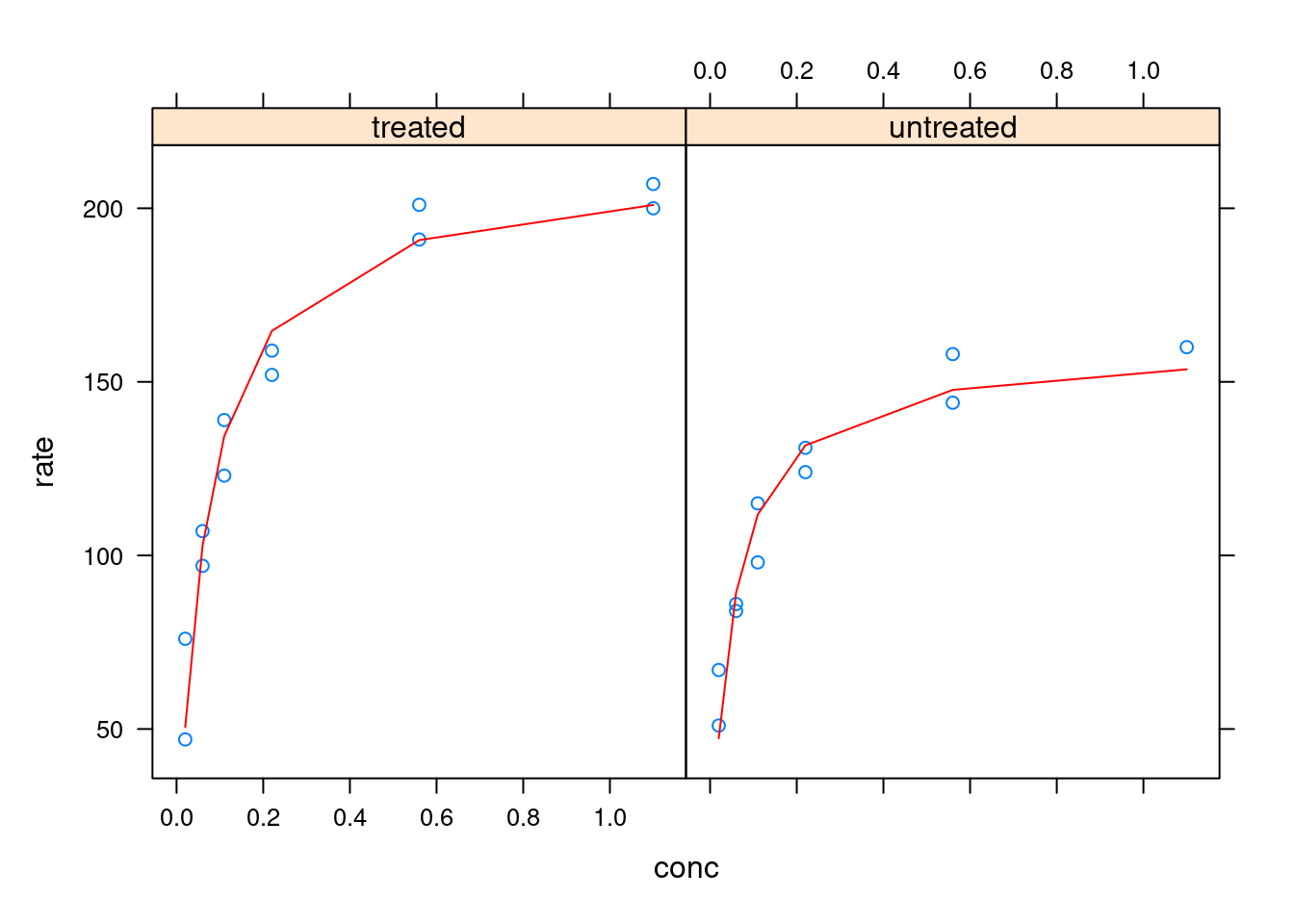

Figura 6.10: Plotagem e análise com Lattice - ajuste externo e paineis.

      Das muitas diferenças que os pacotes ggplot2 e Lattice apresentam, há uma que vale a pena ressaltar. Como visto acima, o ggplot2 realiza o ajuste não linear dentro da linha de comandos de geração do gráfico, ao passo que o Lattice permite fazê-lo fora da linha. Isso é inerente do ggplot2, uma biblioteca desenhada para a produção de gráficos, e não para análises computacionais. Dessa forma o algoritmo que permite o ajuste não linear pelo ggplot2, ainda que seja o mesmo ‘nls’ já trabalhado, não expressa seus resultados explicitamente (embora haja formas de “pescá-los” utilizando-se outros pacotes).
      De certa forma, ainda que o Lattice exija uma curva de aprendizado menos intutiva, ele permite que se utilize os resultados estatísticos obtidos anteriormente para inclusão no algoritmo de plotagem. Isso é vantajoso quando se deseja outros algoritmos estatísticos para ajuste, como acima, ou mesmo sua flexibilização, além do ‘nls’ incluido em ggplot2. Não obstante, o Lattice também permite que se inclua a linha de ajuste dentro do próprio algoritmo, como abaixo:

xyplot(rate ~ conc | state, data = Puromycin,
       panel = function(x, y, ...) {
         panel.xyplot(x, y, ...)
         n3<-nls(y ~ Vmax*x/(Km+x), data=Puromycin, start=list(Vmax=200, Km=0.1))
         panel.lines(seq(0.02,1.1,0.02), predict(n3,newdata=data.frame(x=seq(0.02,1.1,0.02))), col.line = 2)
       },
       xlab = "conc", ylab = "rate")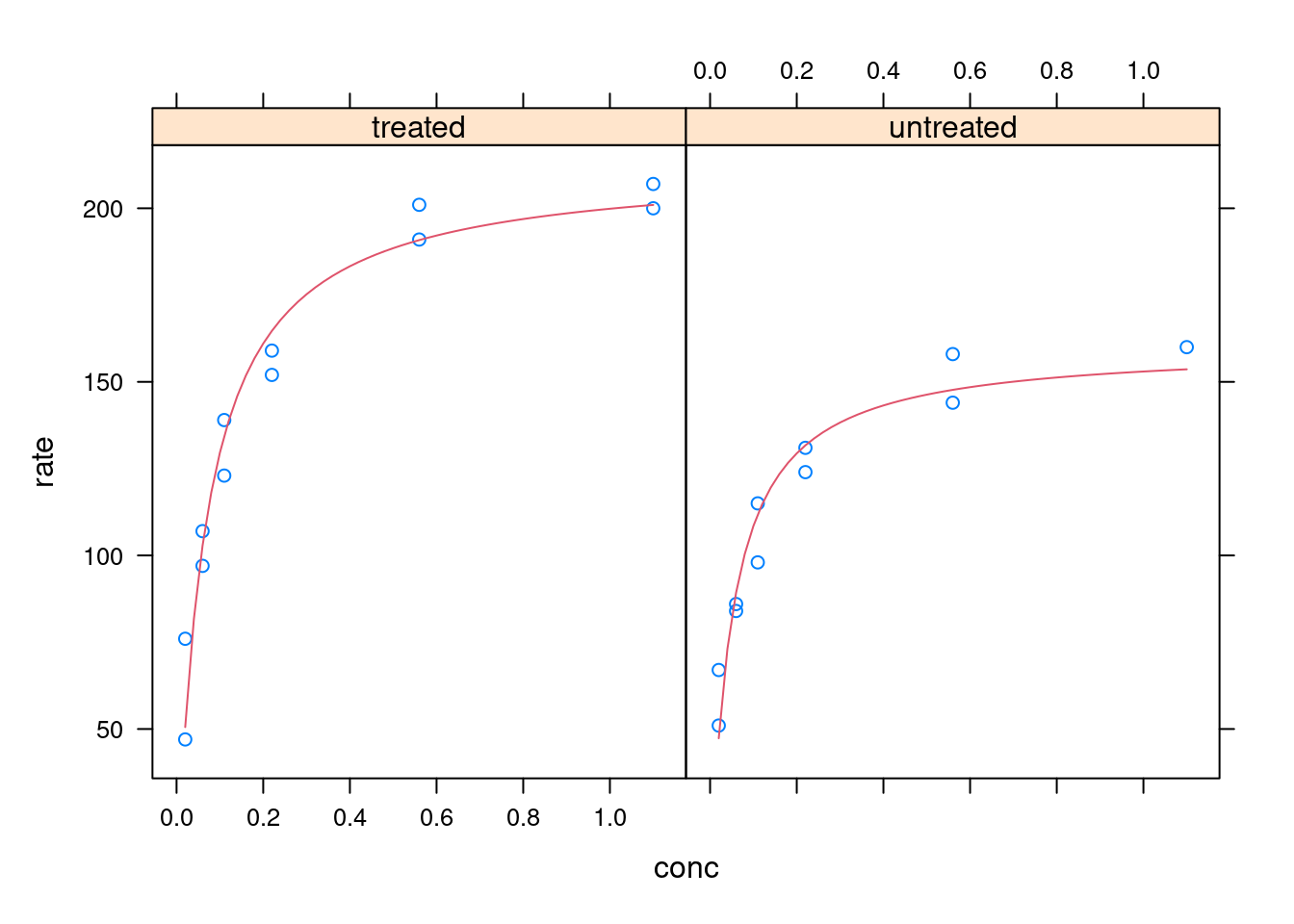

Figura 6.11: Plotagem e análise com Lattice - ajuste interno e paineis.

6.4 Solução Numérica Para o Equilíbrio de Complexos Ligante-Proteína

      Como visto no capítulo 3, por vezes uma solução numérica pode ser empregada quando a solução analítica não converge, ou quando estamos diante de uma equação mais complexa. Nesse sentido a formação de complexos de que trata este subtítulo pode também ser tratada por uma solução numérica.
      Usualmente o tratamento dado para a solução numérica envolve encontrar as raízes de uma equação ou sistema de equações, ou seja:

$$\begin{array}{}F\left(x\right)=0& \text{(6.8)}\end{array}$$ $$\begin{array}{}P+L\rightleftarrows PLKd=\frac{\left[P\right]\left[L\right]}{\left[PL\right]}Então,\left[PL\right]=\frac{\left[P\right]\left[L\right]}{Kd}& \text{(6.9)}\end{array}$$ $$\begin{array}{}\{\begin{array}{c}\left[Pt\right]=\left[P\right]+\left[PL\right]=\left[P\right]+\frac{\left[P\right]\left[L\right]}{Kd}\\ \left[Lt\right]=\left[L\right]+\left[PL\right]=\left[L\right]+\frac{\left[P\right]\left[L\right]}{Kd}\end{array}& \text{(6.10)}\end{array}$$

      Assim, tem-se um sistema de equações lineares nos parâmetros ([P] livre, [L] livre, e complexo [PL]) que pode ser solucionado pelo R por diversas maneiras, uma das quais pela função de minimização rootSolve:

#Cálculo de L, P, e PL em interação biomolecular para 1 conjunto de sítios de mesma afinidade
library(rootSolve) 
Pt =1; Lt=10; Kd=4

# Modelo
model = function(x) c(x[1]+(x[1]*x[2])/Kd-Pt,x[2]+(x[1]*x[2])/Kd-Lt,Pt-x[1]-x[3])
# o modelo acima deve conter uma lista de equações cuja igualdade é zero, ou seja, f(x)=0
(ss=multiroot(model,c(1,1,1))) # comando de execução do rootSolve (sementes pro algoritmo)

## $root
## [1] 0.3 9.3 0.7
## 
## $f.root
## [1] 5e-08 5e-08 5e-12
## 
## $iter
## [1] 5
## 
## $estim.precis
## [1] 4e-08

      Dessa forma os valores resultantes (f.root) quando [Lt] = 10 são apresentados como [P] = 0,3, [L] = 9,3 e [PL] = 0,7.

      Outras soluções numéricas permitem um maior controle sobre o algoritmo empregado, tais como a função optim do R (limites de busca da solução, emprego de vetores, por ex). Para isso será exemplificado a mesma situação acima, embora apresentando uma variação do formalismo que relaciona P, L e PL :

$$\begin{array}{}\{\begin{array}{c}\left[PL\right]=\left[Pt\right]-\left[L\right]\\ \left[PL\right]=\left[Lt\right]-\left[L\right]\\ \left[P\right]\ast \left[L\right]=Kd\ast \left[PL\right]\end{array}& \text{(6.11)}\end{array}$$

      Dessa forma pode-se contruir uma relação quadrática envolvendo as três incógnitas:

$$\begin{array}{}\left(\right[Pt]-[L]-[PL]{)}^2+(\left[Lt\right]-\left[L\right]-\left[PL\right]{)}^2+\left(\right[P]\ast [L]-Kd\ast [PL]{)}^2& \text{(6.12)}\end{array}$$

      Aplicando-se o algoritmo de minimização optim do R:

#Cálculo de L, P, PL em interação para 1 sítio

model2=function(x,Pt,Lt,K){L=x[1];P=x[2];PL=x[3];(Pt-P-PL)^2+(Lt-L-PL)^2+(P*L-Kd*PL)^2} # declaração da função
Pt=1;Lt=10;Kd=4 # parâmetros da função
sol2num = optim(c(0.5,1,.5),model2,method="L-BFGS-B",lower=c(0,0,0),upper=c(Lt,Pt,Pt),Pt=Pt,Lt=Lt) # método BFGS permite bounds (lower, upper)    
sol2num$par # LF, PF, PL calculados

## [1] 9.3 0.3 0.7

      Perceba que são os mesmos resultados anteriores, embora com maior controle da solução. Agora pode-se utilizar essa minimização para criar um vetor de soluções para as três quantidades, como segue:

#Declaração da função
bind1=function(x,Pt,Lt,Kd) {
  L=x[1];P=x[2];PL=x[3];
  (Pt-P-PL)^2+(Lt-L-PL)^2+(P*L-Kd*PL)^2
}

#Parâmetros da função
Pt = 1; Lt = c(5,10,20); Kd = 4

#Minimização (parâmetros para que a função acima dê zero)
y = function(i) optim(c(1, 1, 1), bind1, method =
                        "L-BFGS-B", lower = c(0,0,0), upper = c(Lt[i], Pt,
                                                                Pt), Lt=Lt[i], Pt=Pt, Kd=Kd)

# Resultados em matriz
ypar = function(i) y(i)$par
yp = matrix(nrow=length(Lt), ncol=2+length(Kd),
            byrow=T)
for (i in 1:length(Lt)) yp[i,]=y(i)$par
colnames(yp) = c("L","P","PL")
rownames(yp) = c("5","10","20")
yp

##     L   P  PL
## 5   4 0.5 0.5
## 10  9 0.3 0.7
## 20 19 0.2 0.8

6.5 Cinética de Interação Ligante-Proteína e Solução Numérica

      Sob o mesmo princípio da solução numérica apresentada no ítem anterior para o equilíbrio da interação ligante-proteína, o R permite solução de mesma natureza para a cinética da formação dos complexos, ou seja, os teores de P, L e PL observados no tempo. Nesse caso pode-se desenvolver outras relações a partir da Eq. (6.1). Tomando-se por base que no equilíbrio as taxas cinéticas de k${}_{on}$ e k${}_{off}$ se igualam (steady-state), pode-se relacionar algumas equações diferenciais para a associação, bem como para a dissociação dos complexos:

$$\begin{array}{}Paraaassociação:\{\begin{array}{c}\frac{d\left[PL\right]}{dt}=k_{on}\ast \left[L\right]\ast \left[P\right]\\ \frac{d\left[L\right]}{dt}=-k_{on}\ast \left[L\right]\ast \left[P\right]\\ \frac{d\left[P\right]}{dt}=-k_{on}\ast \left[L\right]\ast \left[P\right]\end{array}& \text{(6.13)}\end{array}$$ $$\begin{array}{}Paraadissociação:\{\begin{array}{c}\frac{d\left[PL\right]}{dt}=-k_{off}\ast \left[PL\right]\\ \frac{d\left[L\right]}{dt}=k_{off}\ast \left[PL\right]\\ \frac{d\left[P\right]}{dt}=k_{off}\ast \left[PL\right]\end{array}& \text{(6.14)}\end{array}$$

       Assim, as taxas globais resultantes para cada quantidade (taxa líquida) envolverá a soma das taxas de associação e dissociação de cada:

$$\begin{array}{}Taxaslíquidas:\{\begin{array}{c}\frac{d\left[PL\right]}{dt}=k_{on}\ast \left[L\right]\ast \left[P\right]-k_{off}\ast \left[PL\right]\\ \frac{d\left[L\right]}{dt}=-k_{on}\ast \left[L\right]\ast \left[P\right]+k_{off}\ast \left[PL\right]\\ \frac{d\left[P\right]}{dt}=-k_{on}\ast \left[L\right]\ast \left[P\right]+k_{off}\ast \left[PL\right]\end{array}& \text{(6.15)}\end{array}$$

      A solução para esse sistema final de equações diferenciais (taxas líquidas) envolve resolver a variação de cada quantidade ($\Delta$x) num determinado intervalo de tempo ($\Delta$t), tal que:

$$\begin{array}{}\Delta x=f\left(x\right)\ast \Delta t& \text{(6.16)}\end{array}$$

      Para isso é necessário utilizar uma biblioteca do R que permita a solução de um sistema de equações diferenciais. Entre as muitas soluções (odeintr, pracma, rODE), o emprego da biblioteca deSolve, que utiliza uma função para integração do sistema por algoritmo de Runge-Kutta de 4a. ordem:

# Cinética de interação ligante-protéina para 1 conjunto de sítios
library(deSolve)

# Condições experimentais
tempo = seq(0, 100) # intervalo de tempo
parms = c(kon=0.02, koff=0.001) # parâmetros do estado estacionário da interação (uM^-1*s^-1 e s^-1, respectivamente)
val.inic = c(L=0.8, P=1, PL=0) # valores iniciais, uM

# Integração do sistema por Runge-Kutta de 4a. ordem
solNumKin = function(t, x, parms) { 
  # definição da lista de parâmetros
  L  = x[1] # ligante 
  P  = x[2] # proteína
  PL = x[3] # complexo
  
  with(as.list(parms),{ 
    # definição da lista de equações diferenciais
    dL = -kon*L*P + koff*PL
    dP = -kon*L*P + koff*PL
    dPL = kon*L*P-koff*PL
    res<-c(dL, dP, dPL)
    list(res)
  })
}

sol.rk4 = as.data.frame(rk4(val.inic, tempo, solNumKin,
                            parms)) # rotina para Runge-Kutta 4a. ordem

# Gráfico
plot (sol.rk4$time, sol.rk4$L, type="l", xlab="tempo",ylab="[composto], uM")
legend("topright",c("L","P","PL"),text.col=c("black","red","blue"),bty="n",lty=c(1,2,3))
lines (sol.rk4$time, sol.rk4$P, type="l", lty=2,col=2,lwd=1.5)
lines (sol.rk4$time, sol.rk4$PL, type="l", lty=3,col=3,lwd=1.5)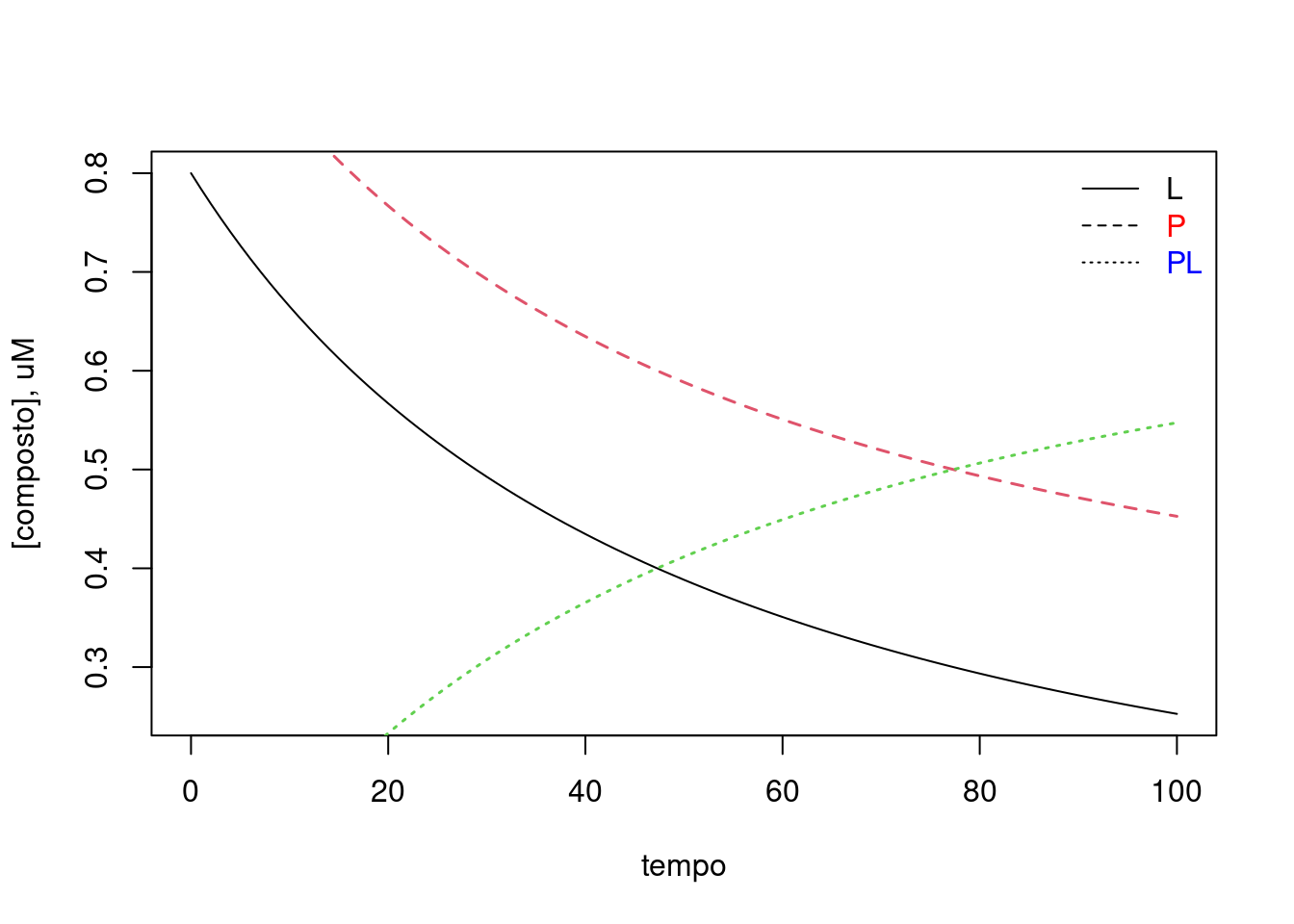

Figura 6.12: Teores de ligante e proteína livres (L e P), bem como do complexo PL apresentados ao longo do tempo de acordo com o método Runge-Kutta de 4a. ordem para solução de equações diferenciais.

References

Dahlquist, FW. 1978. “[13] the Meaning of Scatchard and Hill Plots.” Methods in Enzymology 48: 270–99.

Parsons, DL, and JJ Vallner. 1978. “Theoretical Models for Cooperative Binding—i. One-Site Creator of Binding Sites.” Mathematical Biosciences 41 (3-4): 189–215.

Sarkar, Deepayan. 2008. Lattice: Multivariate Data Visualization with r. Springer Science & Business Media.

Wickham, Hadley. 2011. “Ggplot2.” Wiley Interdisciplinary Reviews: Computational Statistics 3 (2): 180–85.