# Argumentos para uma função
args(curve)function (expr, from = NULL, to = NULL, n = 101, add = FALSE,
type = "l", xname = "x", xlab = xname, ylab = NULL, log = NULL,
xlim = NULL, ...)
NULLSistema tampão biológicos
Sistema acetato
A titulação de um ácido fraco é baseada na equação de Henderson-Hasselbach como segue [@po2001henderson] :
\[\begin{equation} pH = pKa + log\frac{[A^-]}{[HA]} \label{hender-hassel} \end{equation}\]
Ocorre que podemos tratar os teores de \(A^-\) e \(HA\) não em termos absolutos, mas como frações, tanto de base (fb), como de ácido (fa), tal que:
\[\begin{equation} fa+fb=1 \label{frac-tit} \end{equation}\]
Assim, pode-se definir que após uma certa quantidade de base, o valor inicial de HA, em fração unitária, será de 1-fb; dessa forma, a expressão de Henderson-Hasselbach pode ser escrita como:
\[\begin{equation} pH = pKa + log\frac{fb}{1-fb} \label{HH-frac} \end{equation}\]
A partir dessa dedução, pode-se facilmente relacionar que:
\[\begin{equation} fb = \frac{10^{(pH-pKa)}} {1+10^{(pH-pKa)}} \label{HH-fb} \end{equation}\]
E, da mesma forma, pode-se encontrar fa como
\[\begin{equation} fa = 1- fb \label{HH-fb2} \end{equation}\]
Resultando em
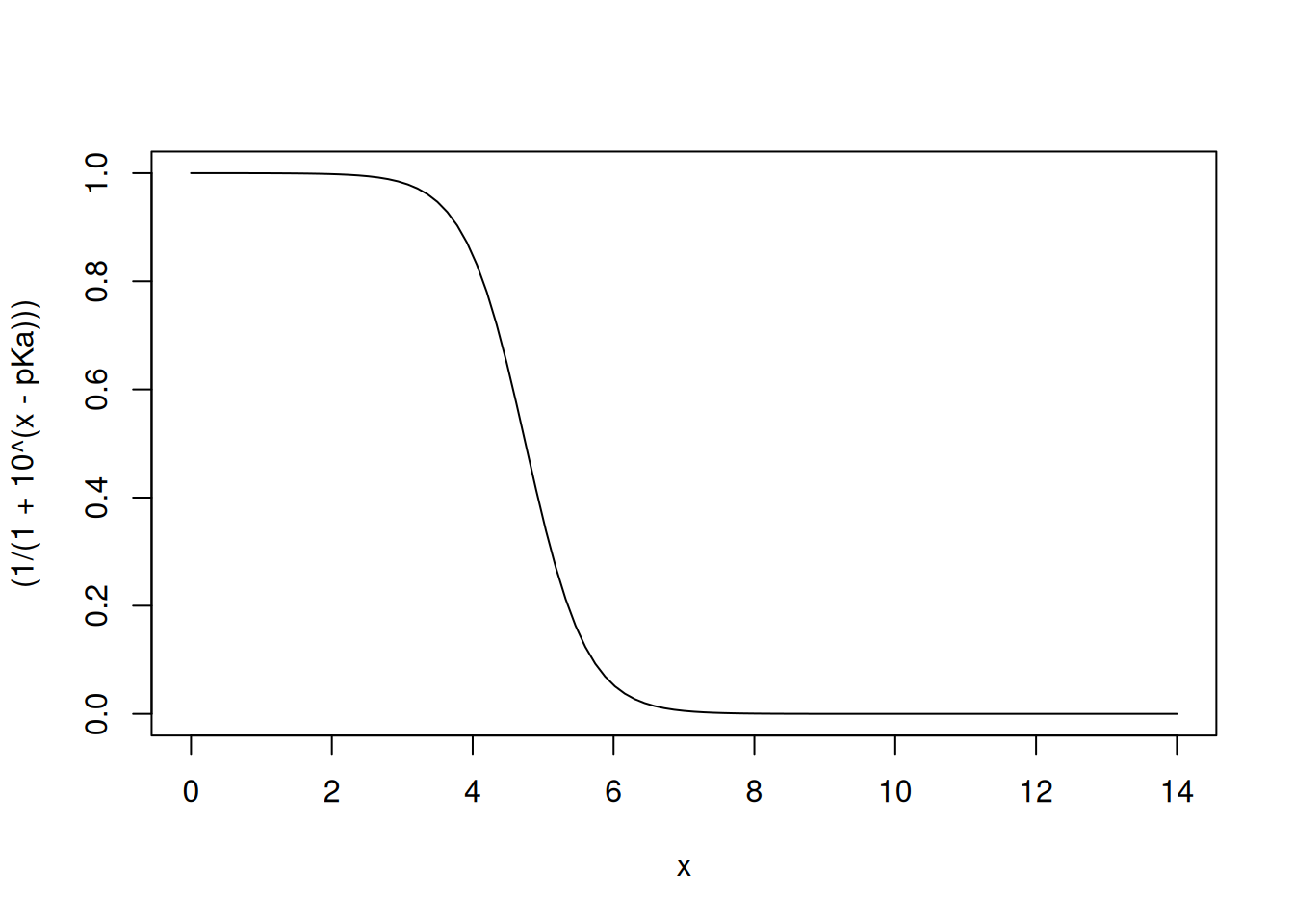
\[\begin{equation} fa = \frac{1}{1+10^{(pH-pKa)}} \label{eq-HH-fa} \end{equation}\]
Dessa forma é possível simular pelo R uma curva de titulação de um ácido fraco qualquer baseando-se em seu valor de pKa. Com exemplo em meio de acetobactérias, podemos exemplificar o tampão acetato, com valor de pKa de 4,75. Para isso utiliza-se a função
curve a partir de seus argumentos (args), como segue:Ou, de forma mais simples:
# Curva de titulação para o sistema acetato/ácido acético
pKa = 4.75
curve((1/(1+10^(x-pKa))),0,14)
Também pode-se fazer o inverso, elaborando um gráfico com a fração fb:
# Curva de titulação para o sistema acetato/ácido acético
pKa = 4.75
curve(((10^(x-pKa))/(1+10^(x-pKa))),0,14)
Sistema bicarbonato
Com o procedimento acima pode-se também simular a curva de titulação para o sistema bicarbonato de tamponamento sanguíneo com base nos valores de pKa do par ácido-base conjugado, apenas somando-se as expressões na equação \(\eqref{eq-HH-fa}\), tal que:
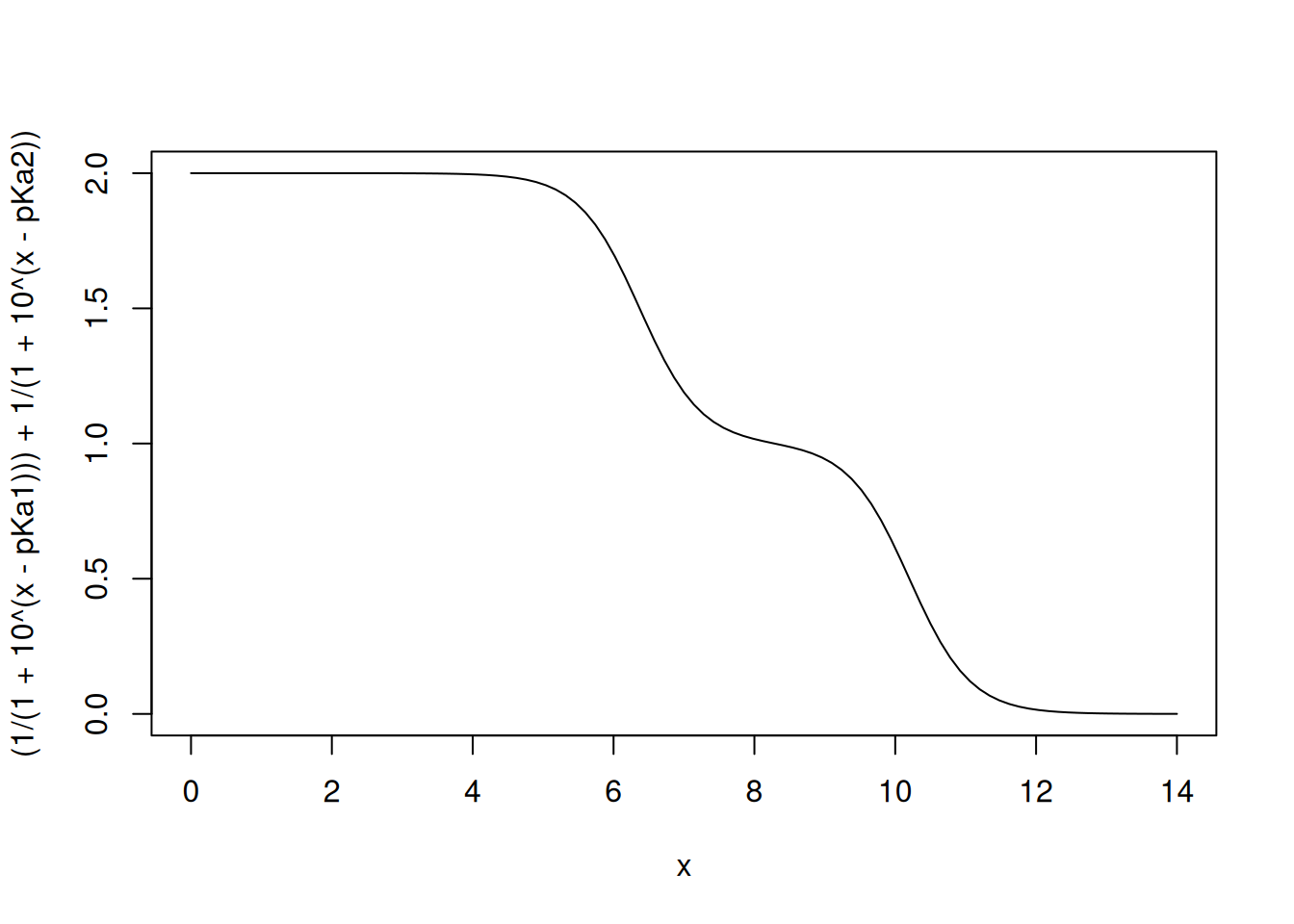
\[\begin{equation} fa = \frac{1}{1+10^{(pH-pKa1)}}+ \frac{1}{1+10^{(pH-pKa2)}} \label{HHbic} \end{equation}\]
Assim,
pKa1 = 6.37
pKa2 = 10.20
curve((1/(1+10^(x-pKa1)))+1/(1+10^(x-pKa2)),0,14)
O gráfico da Figure 1 pode ser armazenado em formatos, utilizando-se, por exemplo, o comando
dev.copy:dev.copy(pdf,"titBicarb.pdf",width=6, height=3) # alternativamente, bmp,
# jpeg, tiff, svg, png E é claro que, partindo-se dos argumentos da função
curve acima, e da flexibilidade que o pacote interno Graphics do R possibilita, pode-se elaborar uma curva mais complexa, como segue:pKa1 = 6.37
pKa2 = 10.20
curve((1/(1+10^(x-pKa1)))+1/(1+10^(x-pKa2)),0,14,
xlab="pH",ylab="fa",
main="Titulação de Ácido carbônico, H2CO3/HCO3-",
type="o", n=50,lwd=2,lty="dotted",
pch=3,col="blue",cex=1.2) # gráfico de titulação
text(4.7,1.3,"pKa = 6,37") # inserção de texto no gráfico
text(9,0.3,"pKa = 10,20")
abline(0.5,0, lty="dotted") # linha pontilhada em intercepto
# e inclinação específicos
abline(1.5,0, lty="dotted")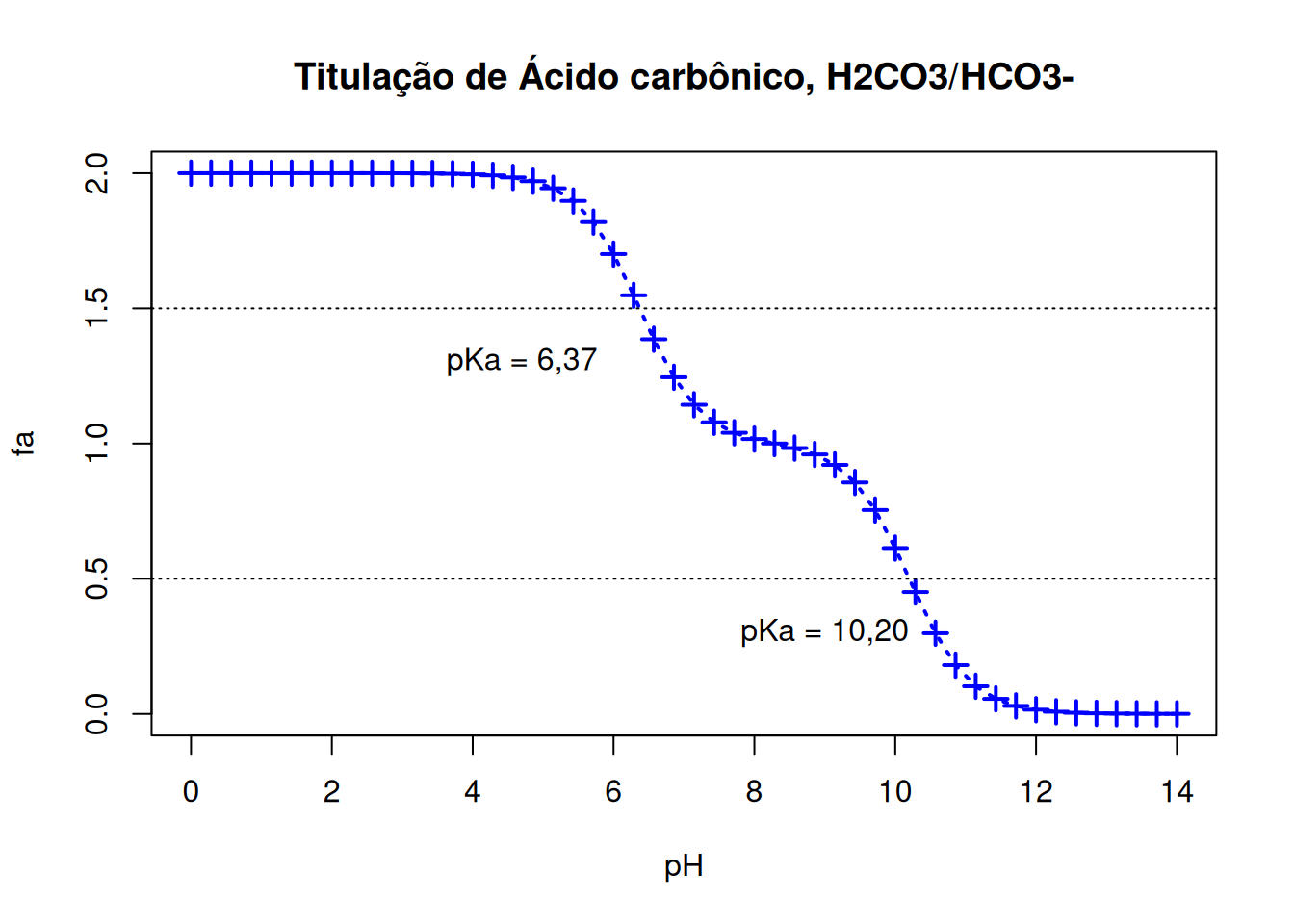
A título de ilustração é possível “recuperar” o valor de pKa fisiológico acima, ou seja, pKa1, utilizando-se o comando
locator(). Como trata-se de um ponto apenas no gráfico, basta digitar o código locator(1) e clicar com o botão esquerdo do mouse no ponto da curva correpondente à fração de 0,5 para fa.locator(1) # para mais pontos no gráfico, basta aumentar o valor entre parênteses Observe que à medida em que o valor de pH aproxima-se do de pKa, a crescente variação em fa parece afetar cada vez menos a variação em pH. Isto é a “alma” do sistema tampão, que permite aos organismos resistirem a variações de pH tanto quanto essas estiverem próximas do valor de pKa correspondentes (bicarbonato, fosfato, proteínas).
Enquanto o sistema bicarbonato possui dois valores de pKa 1 , um dos quais na faixa de tamponamento fisiológico extracelular, o sistema fosfato que atua intracelularmente possui três valores de pKa, embora também atuando em apenas uma faixa fisiológica.
Sistema fosfato
Da mesma forma que simulado para o sistema bicarbonato, podemos elaborar uma curva de titulação para o sistema fosfato de tamponamento, dessa vez considerando seus três valores de pKa correspondentes a cada dissociação do ácido triprótico. Como dantes, a expressão que define a fração fa deverá ser tomada como uma soma algébrica, como segue:
\[\begin{equation} fa = \frac{1}{1+10^{(pH-pKa1)}}+ \frac{1}{1+10^{(pH-pK2)}}+\frac{1}{1+10^{(pH-pKa3)}} \label{eq-HHfosf} \end{equation}\]
No R isso pode ser feito como abaixo: \(\eqref{eq-HHfosf}\)
pKa1=2.2
pKa2=7.2
pKa3=12.7
curve((1/(1+10^(x-pKa1)))+
(1/(1+10^(x-pKa2)))+
(1/(1+10^(x-pKa3))),
xlim=c(1,14),
xlab="pH",ylab="fa",
main="Titulação de tampão fosfato",
sub = " As linhas pontilhadas cruzam os valores de pKa"
)
abline(v=c(2.2,7.2,12.7),col=c("blue","red","green"),lty="dotted") # adição de
# linhas verticais marcando os valores de pKa
text(1.6,2.5,"pKa1")
text(6.5,1.5,"pKa2")
text(11.8,0.5,"pKa3")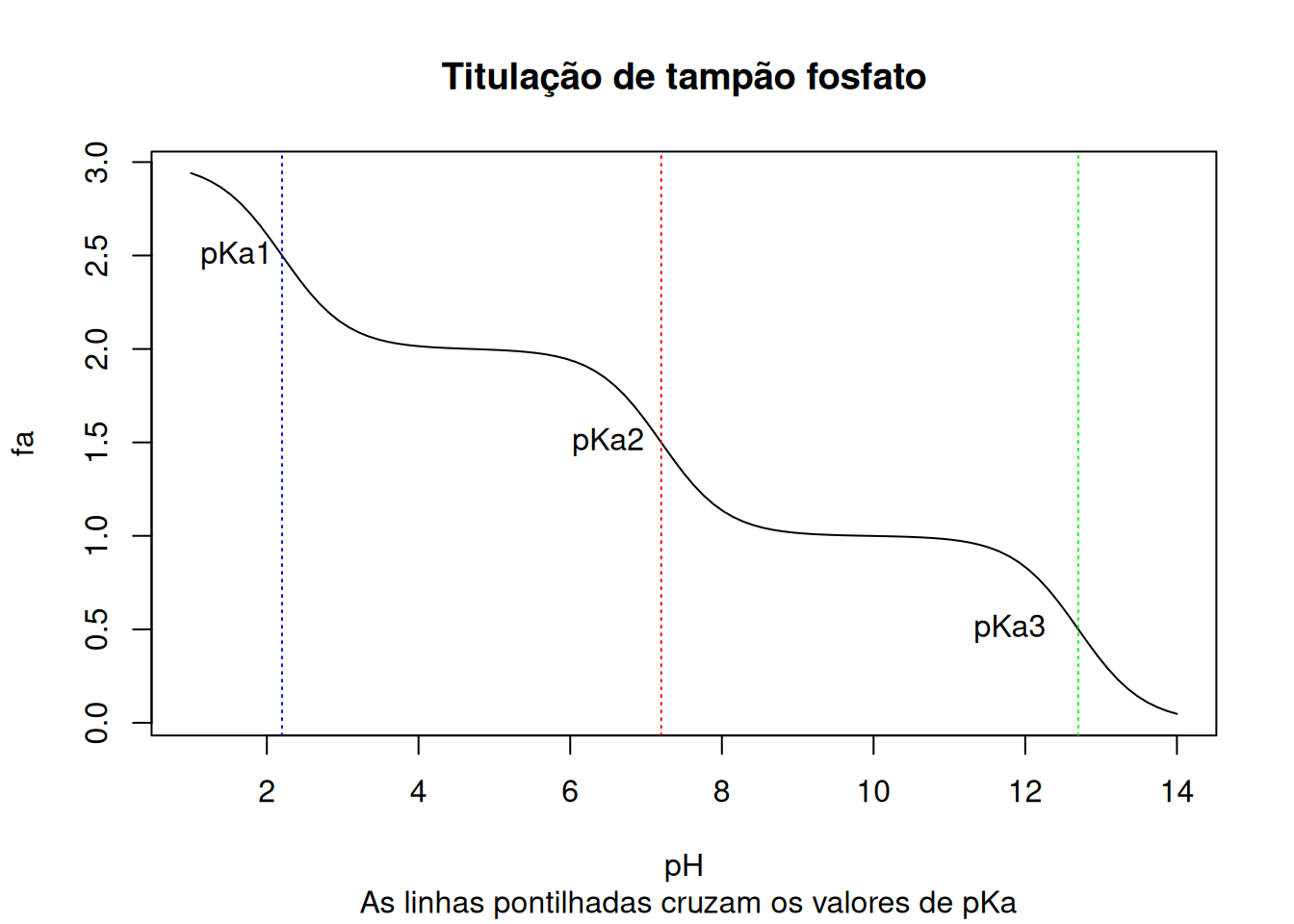
Titulação de sistemas em geral com programação do R
Como ilustrado no fornecimento de argumentos da função args, o ‘R’ é uma linguagem de programação orientada a objeto, e cujos comandos são estruturados como funções. Dessa forma, é possível criar uma função no ‘R’ para operacionalizar ou automatizar qualquer trabalho computacional.
Uma função pode ser criada basicamente pelas instrução que segue:
Uma função pode ser criada basicamente pelas instrução que segue:
função.X <- function( arg1, arg2, arg3 )
{
comandos de execução
return( objeto da função )
} Como exemplo, pode-se criar uma função para converter a temperatura de graus Celsius (C) para temperatura absoluta (K), como segue:
# Função para conversão de graus Celsius a Kelvin
CtoK <- function (tC) {
tK <-tC + 273.15
return(tK)
} Para executar essa função CtoK, basta:
# Executando CtoK:
CtoK (37)[1] 310.15 Tendo isso em mente, também podemos criar uma função que auxilie na elaboração de curvas de titulação, como acima. Essas operações podem ser automatizadas não apenas para o tampão fosfato, mas para qualquer composto sob dissociação em meio aquoso, não importando o número de prótons envolvidos. Para isso, é necessário:
Definir uma função do R que contenha os parâmetros e a operação desejada.
Incluir na função uma estrutura de laço ou loop que permita repetir a operação até exaurido o número de prótons do composto.
Definir um vetor do R contendo os valores dos pKas do composto.
Definir a expressão de curva que viabilize a simulação.
Abaixo é apresentado um modelo de código que permite a simulação para o tampão fosfato.
#Define função e plot de titulação
fa = function(pH,pKa) {
x=0
for(i in 1:length(pKa)) {
x = x+1/(1 + 10^(pH - pKa[i]))}
return(x)
}
pKa=c(2.2,7.2,12.7)
curve(fa(x,pKa),1,14, xlab="pH", ylab="fa",
col=2)
Footnotes
Obs: o valor de pKa do sistema bicarbonato é de 6,8 quando considerado o \(CO_2\) como fonte de ácido carbônico \(H_2CO_3\) em sua reação com \(H_2O\), como por exemplo, para determinação de parâmetros arteriais em analisador hospitalar (\(CO_2\), \(HCO_3^-\), \(O_2\)).↩︎