1. Escolha um tema;
2. Clique na imagem correspondente;
3. Clique em "add";
4. Use o mouse para interatividade e/ou edite o código.
Lembrete: o editor usa desfazer/refazer infinitos no código (Ctrl+Z / Shift+Ctrl+Z) !JSPlotly na Escola
1 Gráficos
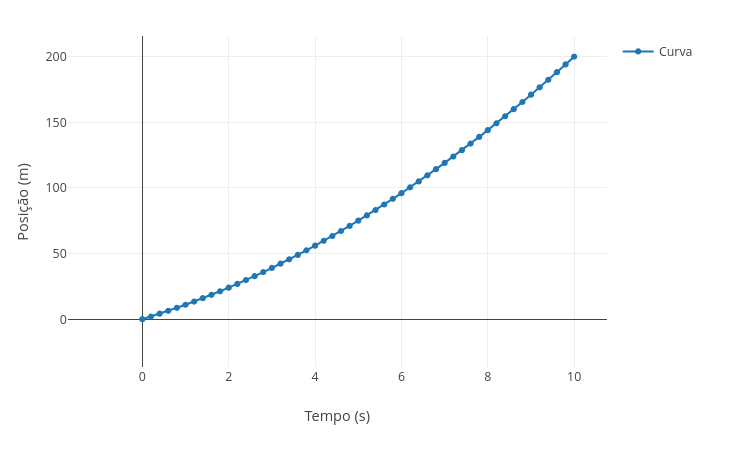
1.1 Simples - MUV (Física)
BNCC: EF09CI03, EM13CNT204, EM13CNT101
Equação:
\[ S(t) = S_0 + v_0,t + \frac{1}{2} a t^2 \]
onde:
- (S(t)) é a posição no instante (t);
- (S_0) é a posição inicial;
- (v_0) é a velocidade inicial;
- é a aceleração constante;
- é o tempo.
\[ v(t) = v_0 + a t \]
Sugestão:
1. Experimente substituir o valor da aceleração e sobreponha o gráfico: "const a = 5", seguido por "add";
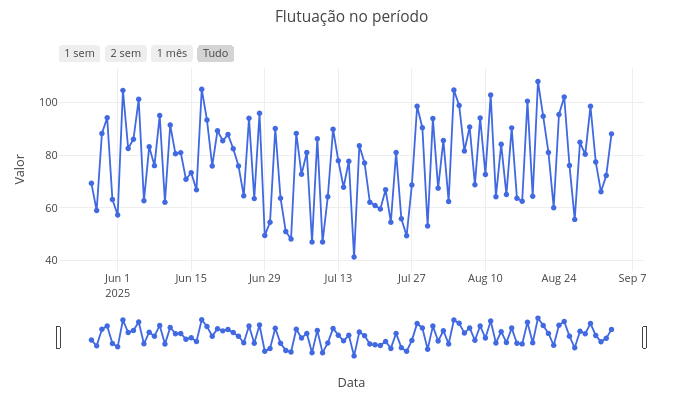
2. Mantenha os dados, mas substitua o valor da velocidade inicial, "const v0 = 3", sobrepondo em seguida.1.3 Uso de seletor e botões em flutuação de dados
BNCC: EF07MA21, EF07GE04, EM13MAT301, EM13CHS104, EM13CNT103
Sugestão:
1. Arraste os marcos de extremidade do gráfico para visualizar um limite mais restrito;
2. Clique nos botões com períodos distintos;
2. Pode-se alterar o ruido aleatório em torno da equação matemática que define a flutuação acima bastando-se modificar a linha de código em: "const valores = dias.map((_, i) => 50 + 10 * Math.sin(i / 10) + Math.random() * 50);" - altere "50" para "5".
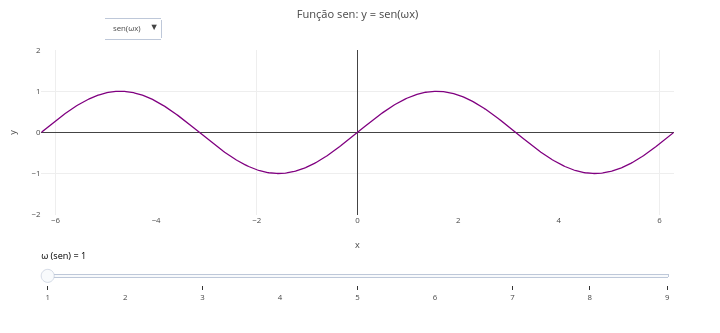
1.4 Barra deslizante para uma função (Matemática)
BNCC: EF07MA20, EF09MA20, EM13MAT302, EM13MAT304
Obs: Esse objeto didático tem um truque…na verdade, dois ! Após clicar em add, é necessário deslizar o slider primeiro para visualizar o gráfico. E para visualizar uma animação para outra equação, é necessário atualizar a página, como orientado na margem inferior da tela gráfica.
Sugestão:
1. Deslize o controle para evidenciar a animação manual;
2. Experimente substituir a equação modelo por outra, e arraste o controle deslizante para observar o efeito;
3. Altere alguns parâmetros para a animação, por exemplo, aumentando os níveis de "frames" (slider.max = "50"; slider.value = 1);
4. Recarregue a página e mude a função matemática; ex: "let f = x => Math.sin(x);"
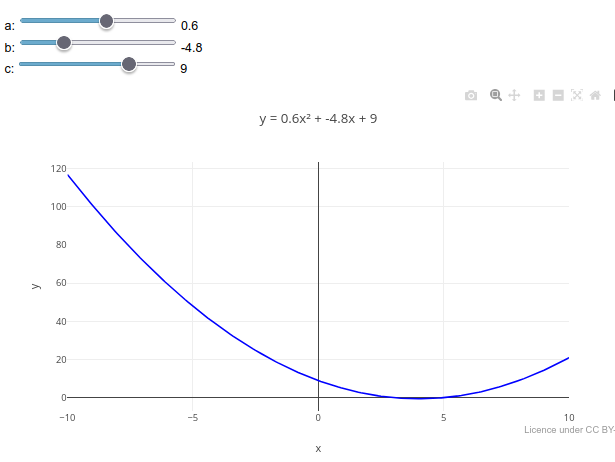
1.5 Múltiplos deslizadores para parábola (Matemática)
BNCC: EF07MA20, EF09MA20, EM13MAT302, EM13MAT304
1. Arraste qualquer slider, e observe a tendência apresentada, bem como a mudança nos parâmetros da equação no topo;
2. Como no exemplo anterior, é possível alterar a função matemática no código, bem como os parâmetros para um novo slider. Teste isso alterando a função " y_values = x_values.map(x => a * x * x + b * x + c);
" para " y_values = x_values.map(x => Math.sin(a * x * x + b * x + c));"1.6 Composição fractal
BNCC: EM13MAT301, EM13MAT305, EM13MAT401, EM13ARM502, EF09MA10
Equação
\[ z_{n+1}=z_{n}^{2}+c \]
Onde:
z ∈ C: geralmente inicializado como o ponto do plano complexo;
c ∈ C: fixo para cada conjunto de Julia.
Sugestão
1. Experimente alterar os componentes Real e Imaginário da fórmula, para obter padrões artísticos distintos. Seguem sugestões:
c = 0 + 0i
c = -0.4 + 0.6i
c = 0.285 + 0i
c = -0.8 + 0.156i
c = 0.45 + 0.1428i
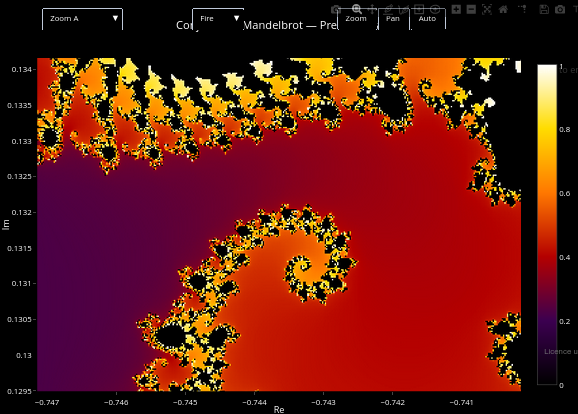
1.7 Fractal de Mandelbrot
Sugestão
1. Selecione cores e níveis de ampliação distintos ("zoom") nos dois menus, para visualizações distintas;
2. Verifique onde se encontram as equações que definem o perfil de Mandelbrot no código, e tece pequenas alterações para verificar resultados distintos.
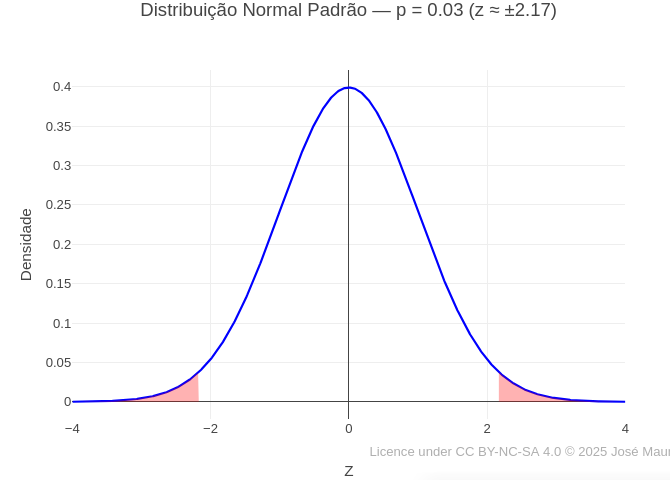
1.8 Curva de distribuição normal (Estatística)
BNCC: EM13MAT316, EM13MAT407, EM13MAT312
Equação
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} \, e^{ -\frac{(x - \mu)^2}{2\sigma^2} } \]
Onde:
- \(\mu\) = 0 (média da distribuição);
- \(\sigma\) = 1 (desvio padrão);
- x = variável aleatória contínua; f = função de densidade da distribuição normal
\[ z = \frac{x - \mu}{\sigma} \]
Sugestão:
1. Experimente alterar o valor de "p" e rodar o gráfico. Esse valor representa a probabilidade de se observar, sob a hipótese nula, um valor tão extremo ou mais extremo do que o observado — ou seja, mede a evidência contra a hipótese nula. No gráfico, representa a área sob a curva normal nas regiões críticas, indicando a chance de ocorrência do resultado observado por puro acaso.
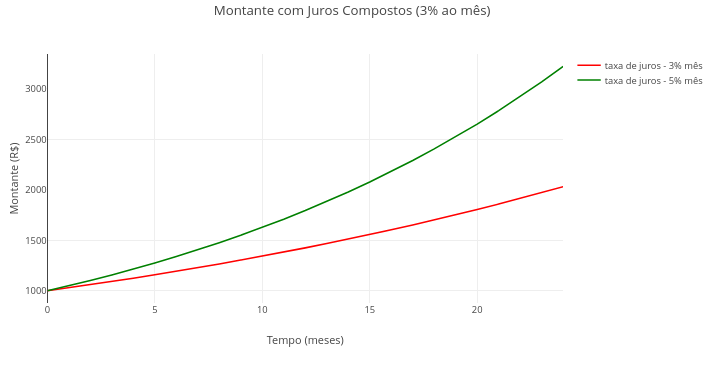
1.9 Juros Compostos (Matemática Financeira)
BNCC: EF09MA05, EM13MAT303, EM13MAT402
Equação:
\[ M = C \cdot (1 + i)^t \]
Onde,
- M: montante final
- C: capital inicial
- i: taxa de juros por período (em decimal)
- t: número de períodos (ex: meses)
Sugestão:
1. Varie o período de contratação, a taxa mensal de juros ou o montante inicial.
2. Experimente combinar os parâmetros na variação.
3. Avalie a diferença visual entre um investimento e um empréstimo, inserido valor positivo de capital inicial para o 1o. e negativo para o 2o.
4. Observe a curva descendente para um empréstimo simulado com capital inicial negativo. Os valores remanescentes referem-se à dívida faltante para quitar o empréstimo.
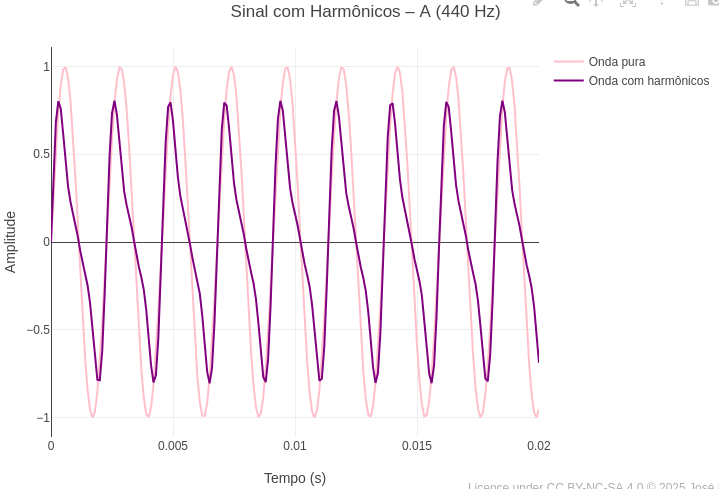
1.10 Altura, harmonia e timbre de sons (Física)
1.10.1 BNCC: EF15AR06, EM13ARH402
Sugestão:
1. Teste outras tonalidades (C,G,D, etc), observando como se apresenta a onda pura sobrepondo os gráficos;
2. Avalie a diferença entre uma onda pura e aquela produzida com instrumentos musicais, envolvendo harmônicos naturais. Para isso, substitua a opção booleana de "false" para "true" na variável "const ondaComposta".
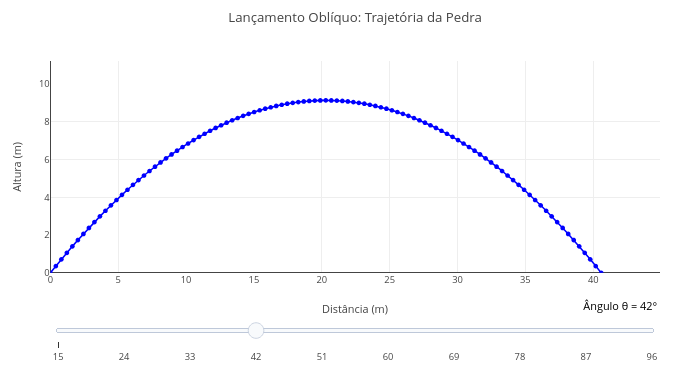
1.11 Lançamento oblíquo (Física)
BNCC: EF09MA07, EM13CNT102, EM13CNT104, EM13CNT302
Equação:
1. Equação geral
\[ y(x) = x \cdot \tan(\theta) - \frac{g}{2 v_0^2 \cos^2(\theta)} \cdot x^2 \]
Onde:
- y(x): altura em função da distância horizontal;
- x: posição horizontal (m);
- \(\theta\): ângulo de lançamento em relação à horizontal (radianos ou graus);
- v0: velocidade inicial do projétil (m/s);
- g: aceleração da gravidade (9,8 m/s²\(^{2}\))
2. Tempo total de vôo:
\[ t_{\text{total}} = \frac{2 v_0 \sin(\theta)}{g} \]
3. Posição Horizontal ao longo do tempo
\[
x(t) = v_0 \cos(\theta) \cdot t
\]
Sugestão:
1. Veja que há uma barra deslizante para ângulos iniciais na simulação. Arraste a barra para outro ângulo e adicione o gráfico, comparando o efeito dessa modificação.
2. Altere a velocidade inicial no código, e observe o efeito no gráfico.
3. Simule uma "condição lunar" para a trajetória, e cuja gravidade é em torno de 1/6 a da Terra (~1.6 m/s²).
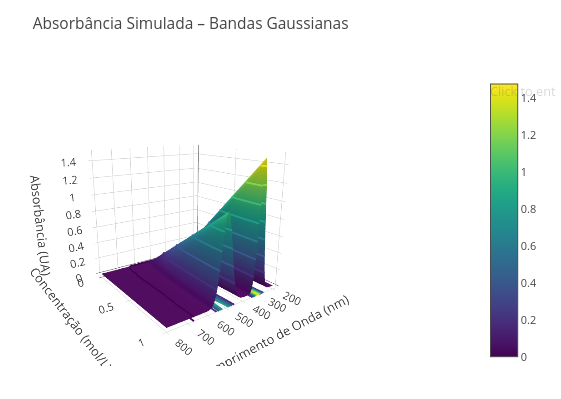
1.12 Gráfico 3D para bandas de absorção em função de concentração (Química)
BNCC: EF09CI04, EF09MA17, EM13CNT103, EM13MAT305
Sugestão
1. Experimente alterar o padrão do gráfico e suas cores. Respectivamente: type: 'surface', colorscale: 'Viridis');
2. Altere a faixa de comprimento de onda, separando os picos; para isso, mude as variáveis min/max de lambda: const lambdaMin = 450, lambdaMax = 600;
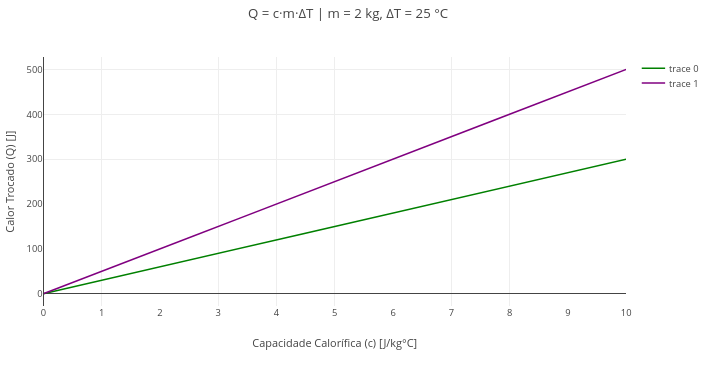
1.13 Capacidade Calorífica (Física)
BNCC: EF09CI06, EM13CNT104, EM13CNT203
Equação:
\[
Q = c \cdot m \cdot \Delta T
\]
Sugestão:
1. Experimente variar inicialmente a temperatura, sobrepondo alguns gráficos;
2. Varie também a massa no editor de códigos, para comparação.
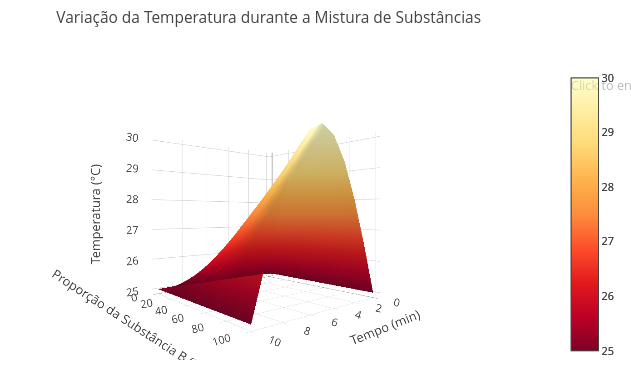
1.14 Gráfico 3D para mistura de substâncias em reação exotérmica (Química)
BNCC: EF09CI02, EM13CNT103, EM13CNT103
Sugestão:
1. Experimente variar inicialmente a temperatura, sobrepondo alguns gráficos;
2. Varie também a massa no editor de códigos, para comparação.
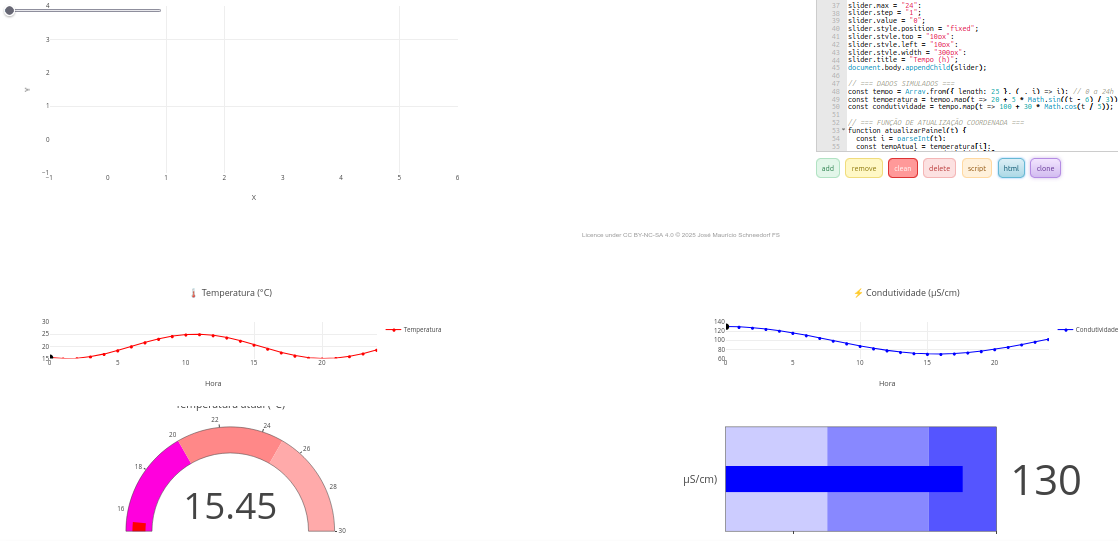
1.15 Painel interativo (dashboard) para medidas ambientais (dados simulados)
BNCC: EF07MA21, EF09MA21, EM13MAT406, EM13LGG604
Sugestão:
1. Ainda que seja um objeto que apenas simula a aquisição de dados, pode-se obter um resultado diferente interferindo-se no código, como:
a. Alteração dos sliders: "slider.min = "0";slider.max = "24"; slider.step = "1" " ;
b. Alteração nas equações que definem o comportamento dos mostradores:
"const tempo = Array.from({ length: 25 }, (_, i) => i); // 0 a 24h
const temperatura = tempo.map(t => 20 + 5 * Math.sin((t - 6) / 3)); // pico 12h
const condutividade = tempo.map(t => 100 + 30 * Math.cos(t / 5)); "
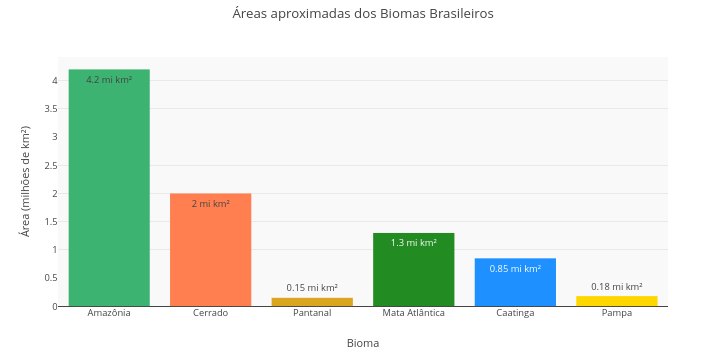
1.16 Área de biomas brasileiros (Biologia)
BNCC: EF05GE05, EF08GE08, EM13CNT301, EM13CNT304
Sugestão
1. Os dados apresentados são apenas para efeito de simulação. Desejando dados mais robustos, recomenda-se fontes seguras (ex: MapBiomas Brasil - https://brasil.mapbiomas.org/)
2. Este é um gráfico de barras, apenas isso. Se você alterar as informações presentes nas constantes dos 3 primeiros vetores ("const X = [...]"), poderá converter a representação para um tema distinto.
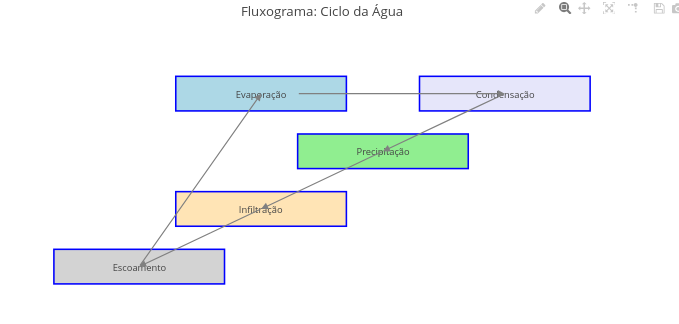
1.17 Diagrama de ciclo da água (Biologia)
BNCC: EF06CI03, EF06CI04, EM13CNT103, EM13CNT202
Sugestão:
1. Como para diagramas acima, experimente alterar no código as propriedades das setas e dos termos e campos envolvidos no fluxograma;
2. Substitua termos para a formação de outro fluxograma;
3. Reposicione os objetos na área gráfica (campos, termos, setas) com auxílio do mouse.
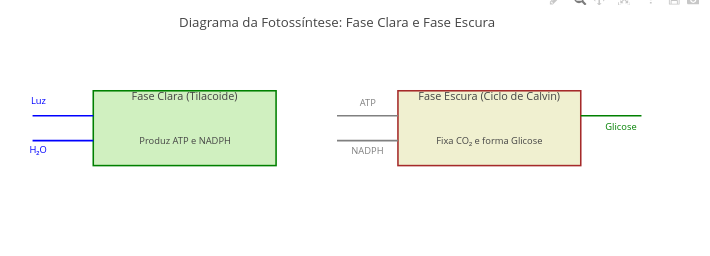
1.18 Fluxograma de ciclos claro e escuro da fotossíntese (Biologia)
BNCC: EM13CNT101, EM13CNT103, EM13CNT201, EM13MAT405
Sugestão
1. Experimente reposicionar as entradas e saídas (ex: Luz, Glicose) por simples arraste de mouse;
2. Substitua os termos dentro dos quadros, ou mude outros aspectos do diagrama (cor, preenchimento, por ex).
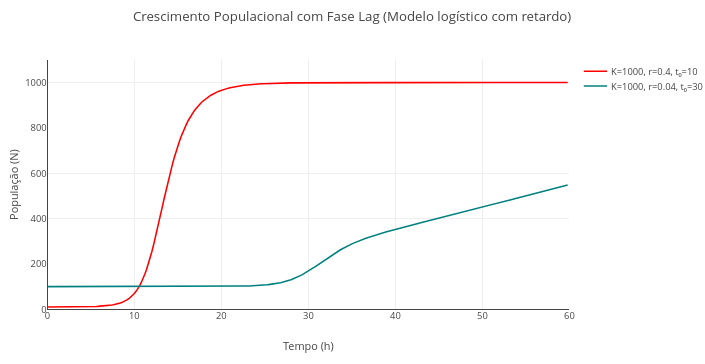
1.19 Modelo de Crescimento Populacional com Fase Lag (Biologia)
BNCC: EM13CNT102, EF06MA17, EF08CI06, EM13MAT301, EM13CNT201
Equação:
\[ N(t) = \frac{K}{1 + \left(\frac{K - N_0}{N_0}\right) \cdot e^{-r \cdot A(t) \cdot t}}, \quad \text{com } A(t) = \frac{1}{1 + e^{-k(t - t_0)}} \]
Onde:
- K = capacidade de suporte ambiental;
- N0 = população inicial;
- r = taxa intrínseca de crescimento;
- A(t) = fator de ativação do crescimento com atraso (fase lag);
- t0 = ponto médio de transição entre fase lag e fase log;
- k = constante de suavidade do retardo (fixado como 0.5 no código)
Sugestão:
1. Experimente variar os parâmetros da equação, combinando alguns, e comparando seus efeitos sobre os gráficos:
a. Capacidade de suporte;
b. População inicial;
c. Taxa de crescimento;
d. Retardo (fase lag);
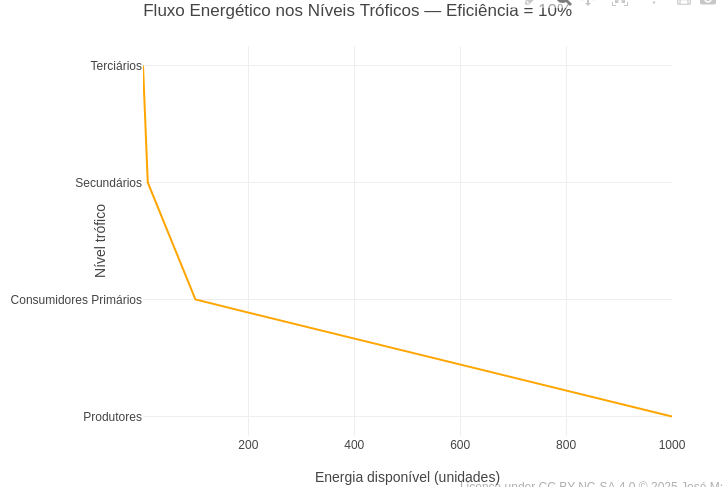
1.20 Eficiência energética e cadeia alimentar (Biologia)
1.20.1 BNCC: EF06CI02, EM13CNT202, EM13CNT203
Sugestão
1. A regra de Lindeman, esboçada na referência acima, estabelece uma variação para 5-20% de eficiência energética no ecossistema. Assim, experimente sobrepor as curvas com tais taxas;
2. Se quiser observar a relação logarítmica da transferência de energia, acrescente o comando "type: 'log'," , logo abaixo de "title: 'Energia disponível (unidades)',".
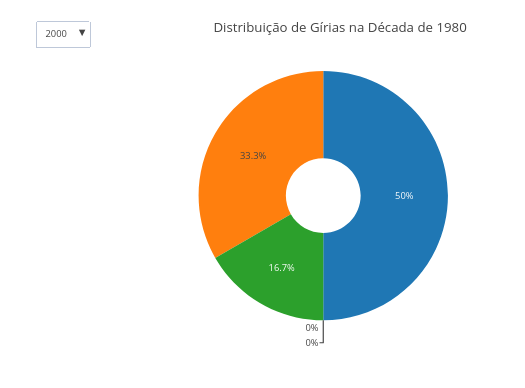
1.21 Gírias faladas no Brasil de 1980-2020 (Linguagens)
BNCC: EF89LP19, EM13LGG102
1. Pode-se usar a passagem de mouse para observar o "tip" (dica) apresentada para cada dado no gráfico.
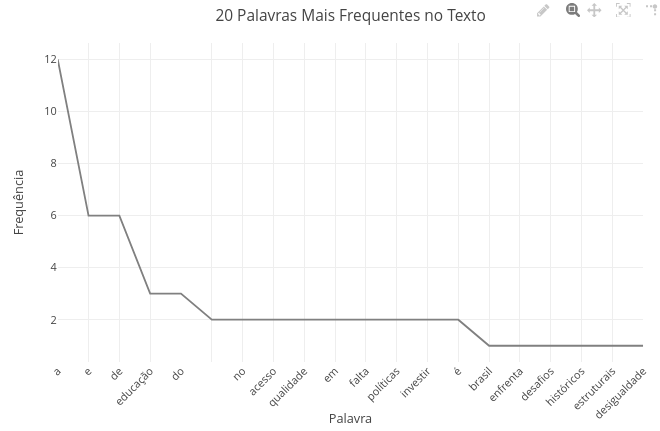
1.22 Frequência de palavras em texto (Linguagens)
BNCC: EM13LGG101, EM13LGG302, EM13LGG303
Sugestão
1. Experimente substituir o texto do código por outro;
2. Experimente variar o quantitativo de termos mais frequentes na variável "const entradas" (opcionalmente, varie também no título do gráfico, para fazer sentido);
3. Compare um texto em português com sua tradução para inglês ou outra língua.
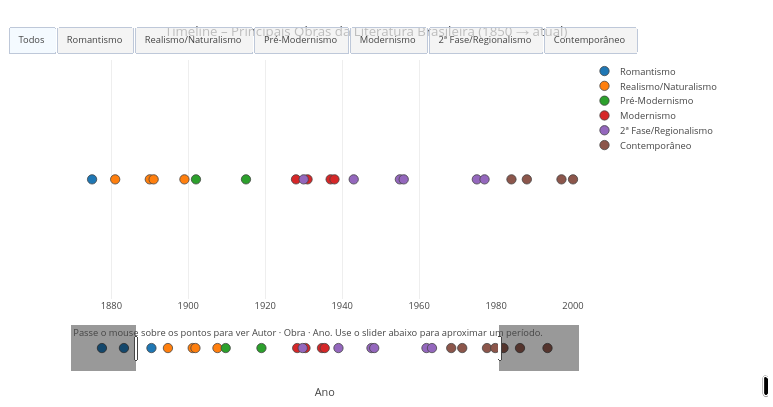
1.23 Obras literárias e movimentos estéticos (Linguagens)
1.23.1 BNCC: EF89LP47, EM13LP01, EM13LP02, EM13LGG201
Sugestão
1. Arraste os marcadores extremos para ampliar o foco em um período específico da lieratura;
2. Altere o script acrescentando outras obras-chave em "const obras =" e "const periodos ="1.24 Criação de objetos 3D (Arte)
BNCC: EF09MA16, EF15AR06, EM13MAT405, EM13LGG604
1. Experimente alterar alguns valores no script, testando o resultado. Por exemplo, crie uma tapete (ou melancia achatada) alterando o código em: "const zVal = L * (t - 0.5)"...para "const zVal = L * (t - 20.5);"
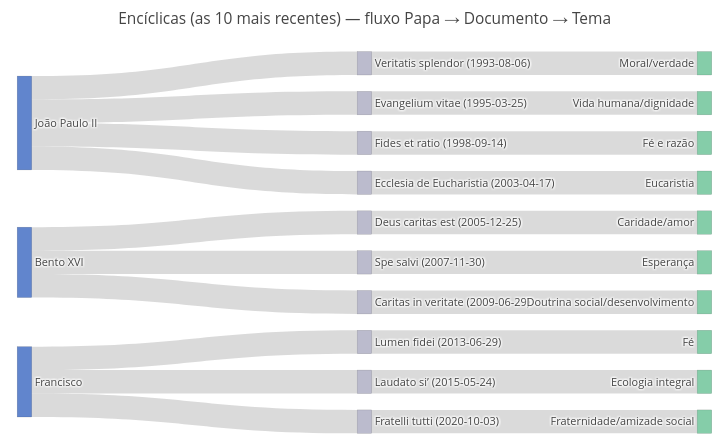
1.25 Diagrama interativo sobre encíclicas papais (Ensino Religioso)
BNCC: EF05ER01, EF09ER02, EM13ER04
Sugestão
1. Para perceber o dinamismo da representação, experimente arrastar qualquer parte do fluxograma, e observe a acomodação das demais;
2. Como dantes, pode-se alterar a informação constante no fluxograma, mantendo suas características gráficas e dinâmicas, bastando-se alterar as constantes utilizadas para gerar o objeto ("const = ").
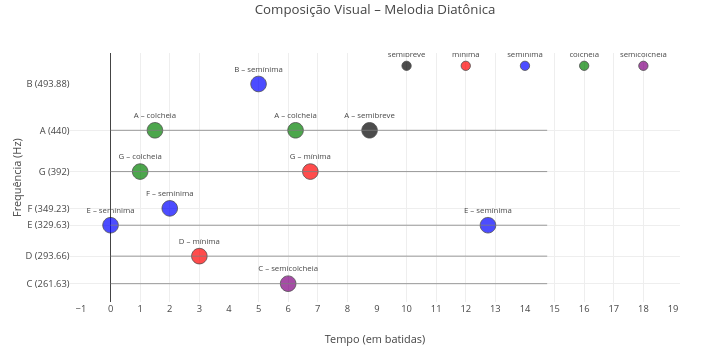
1.26 Editor de notação musical (Arte)
BNCC: EF15AR06, EF69AR22, EM13ARH402
1. Experimente alterar a sequência melódica do código no vetor correspondente;
2. Experimente alterar as figuras de duração no vetor correspondente
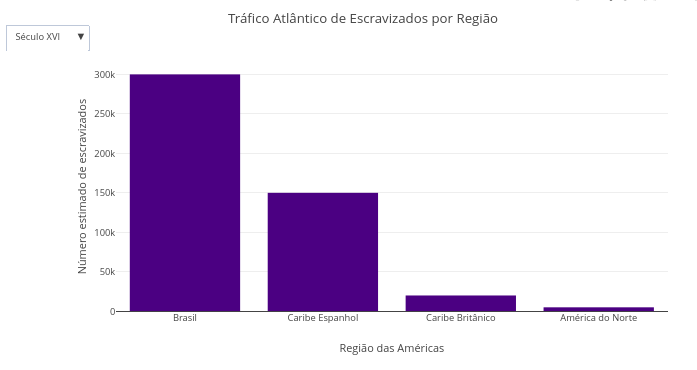
1.27 Distribuição de escravizados nas Américas no período de 1500–1888 (dados simulados; História)
BNCC: EF08HI06, EM13CHS104, EM13CHS503
Sugestão:
1. Experimente alterar entre os períodos no menu suspenso, comparando as estimativas de tráfico escravo;
2. Selecione um período, crie o gráfico, selecione outro período, e adicione outro gráfico. Isso permite comparar o quantitativo de escravos aportados pelas barras duplas formadas, e passagem do mouse sobre cada barra.
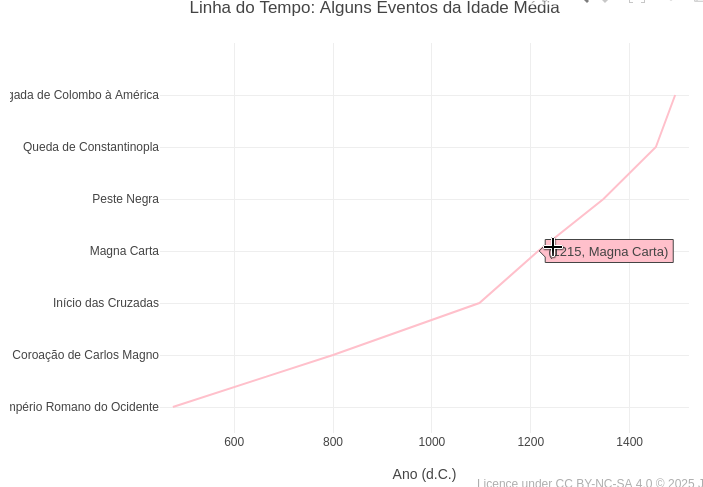
1.28 Linha do tempo para eventos da Idade Média (História)
BNCC: EM13CHS101, EM13CHS102
Fonte: Encyclopedia.com
Sugestão:
1. Experimente alterar no código eventos e períodos, e destinados a outro período da História humana.
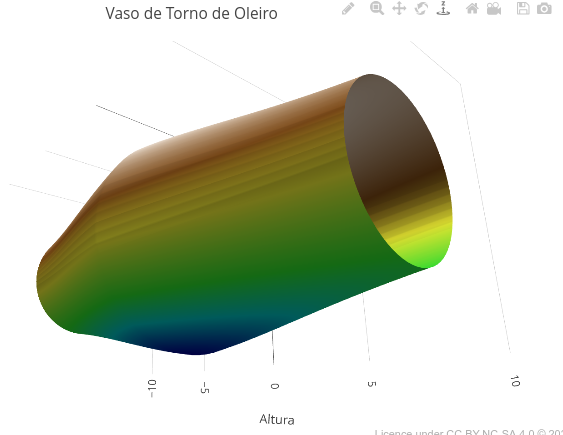
1.29 Vaso de torno de olaria (STEAM)
BNCC: EM13MAT101, EM13MAT403, EM13CNT204, EM13AR01, EM13AR02
1. Altere a altura do vaso, seu formato, e suas cores, editando o código nos campos específicos.1.30 Mini CAD (Computer-Aided Design- STEAM)
BNCC: EM13MAT301, EM13MAT503, EM13MAT402
1. Experimente alterar os parâmetros base, altura e curvatura do código, variando também o sinal dos valores (positivo, negativo);
2. Altere alguma função trigonométrica (linhaX ou linhaY, seno para tangente, por exemplo), e sobreponha ao plot;
3. Sobreponha figuras geométricas com paleta de cores distintas.
4. Crie figuras simétricas sobrepondo uma curva com parâmetro positivo a uma com mesmo parâmetro negativo.
2 Mapas
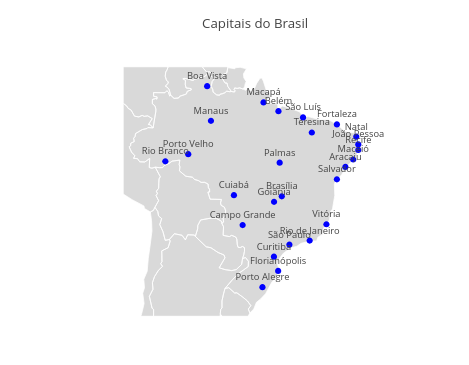
2.1 Mapa do Brasil e Capitais
BNCC: EM13CHS101, EM13CHS202, EM13CHS301
Sugestão:
1. Experimente usar o botão de rolagem do mouse e ícone "pan" da barra superior, para interagir com o mapa.
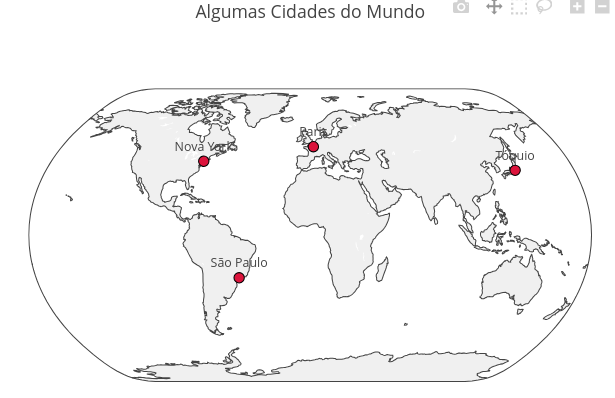
2.2 Mapa mundi com algumas cidades de grande porte
BNCC: EF06GE05, EF07GE06, EM13CHS101, EM13MAT502
1. Experimente alterar o script, inserindo outras cidades com suas respectivas coordenadas geográficas em "const data" (text, long - longitude, lat - latitude)
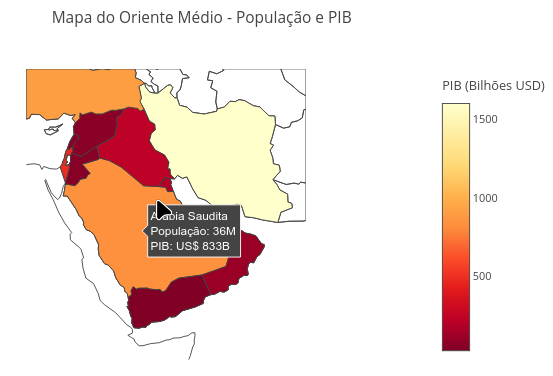
2.3 Mapa e PIB do Oriente Médio
2.3.1 BNCC: EF09GE03, EF08GE06, EM13CHS104, EM13CHS201
Sugestão:
1. Experimente usar o botão de rolagem do mouse;
2. Clique num país para identificar seu nome e produto interno bruto aproximado;;
3. Modique o código para atualizar algum dado, ou para modificar a informação (trocando PIB por outro dado, por ex).
3 Saída de Texto
3.1 Treinamento em JavaScript (Ciências da Computação)
BNCC: EF09LP27, EF06MA20, EM13MAT503, EM13LGG701
Sugestão:
1. Aqui o "céu é o limite" ! Existem inúmeras possibilidades para comandos e funções em JavaScript, bem como para saída conjunta de dados, cálculos e gráficos.
4 Animações
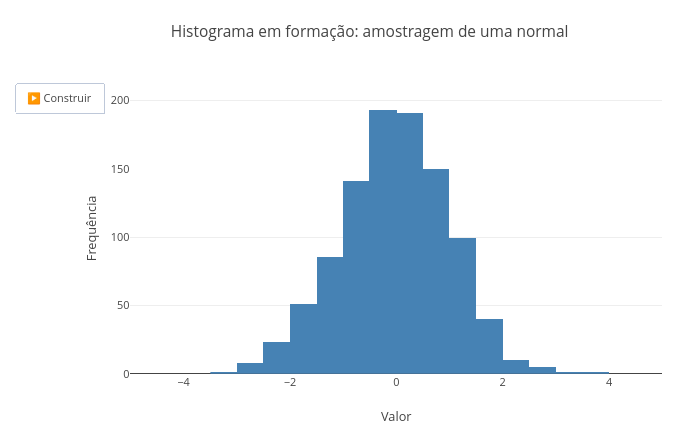
4.1 Histograma (Estatística)
BNCC: EF09MA21, EM13MAT406, EM13MAT407
Sugestão:
1. Observe no topo do script as diversas constantes passíveis de alteração para uma animação distinta, e experimente alterá-las uma a uma para compreender tanto a ação do objeto, como o conteúdo estatístico a que se refere:
const mu = 0 (média);
const sigma = 1 (desvio-padrão);
const n_frames = 50 (no. de quadros);
const sample_per_frame = 20 (taxa de amostras/quadro);
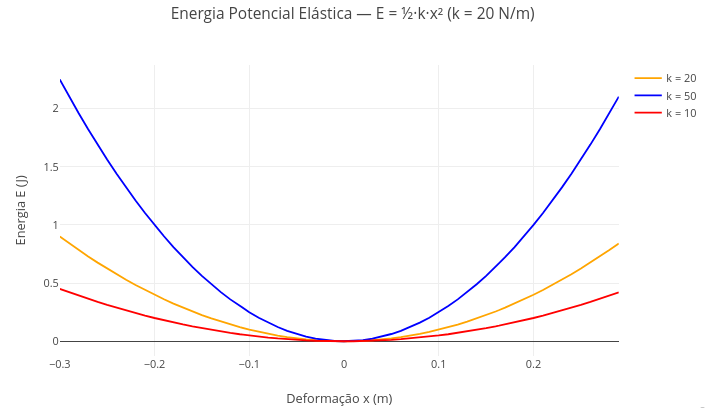
4.2 Energia potencial elástica (Física)
BNCC: EM13CNT102,EM13CNT202, EM13MAT402
Equação
\[ F = -k*x \]
Onde:
- F = força restauradora da mola (N);
- k = constante elástica da mola (N/m);
- x = deformação (m).
\[ E = \frac{1}{2}*k*x^2 \]
Onde:
- E = energia potencial elástica (J).
Sugestão:
1. Experimente alterar o valor da constante elástica da mola para evidenciar seu efeito, relacionando-a com molas mais rígidas ou menos rígidas;
2. Altere os limites de deformação da mola na "estrutura de constrole" do código (ex: "for (let x = -0.7)"), e observe o efeito na energia potencial máxima;
3. Observe que, pela operação quadrática no valor da deformação, a energia potencial é sempre positiva.
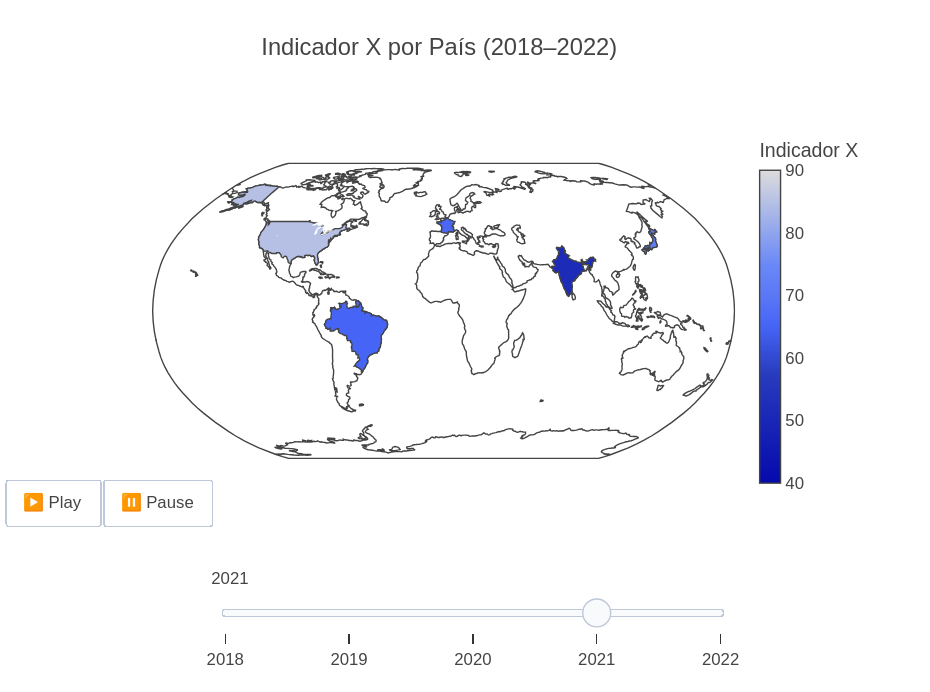
4.3 Alterações cartográficas no tempo
BNCC: EF08GE09, EF07GE05, EM13CHS102, EM13CHS104
Sugestão:
1. Pode-se alterar a formatação do mapa no código para cores ("lakecolor"), posição do menu ("updatemenus"), duração da transição entre frames ("transition"), entre outros;
2. Esse exemplo é genérico; altere as constantes em "paises", "anos", e "valores", e obtenha um novo mapa para um tema específico.
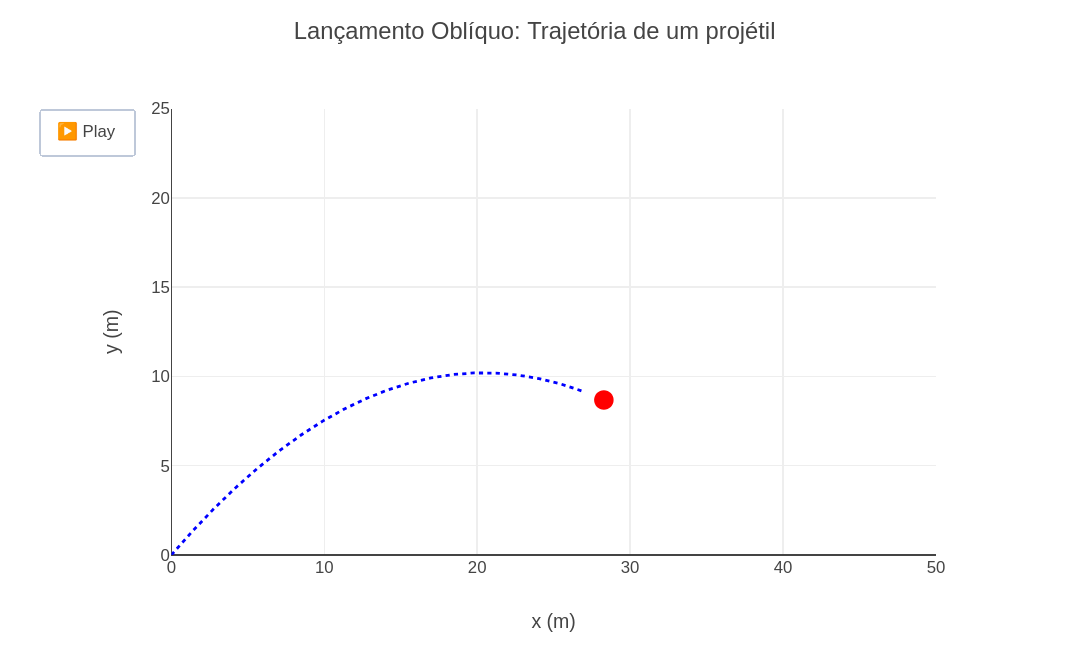
4.4 Lançamento oblíquo
BNCC: EF09CI09, EF09MA20, EM13CNT103, EM13MAT304
Sugestão:
1. Assim como no tópico anterior, experimente alterar parâmetros da equação, tais como a velocidade inicial e o ângulo de ataque, e observar o efeito dessas mudanças.
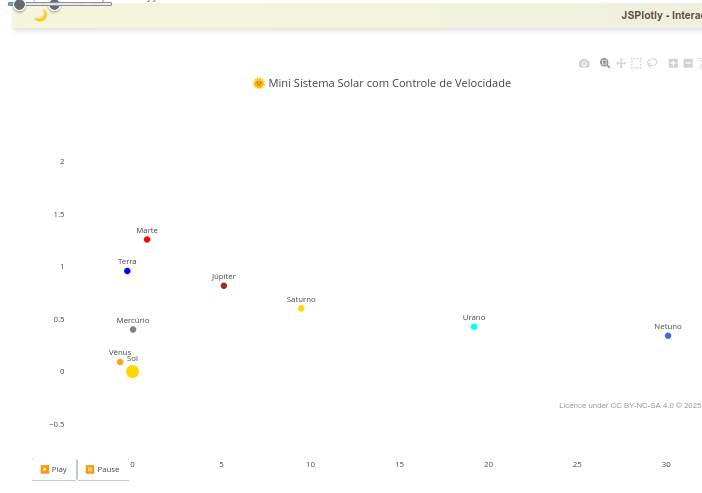
4.5 Movimento de translação em sistema solar
BNCC: EF05CI08, EF07CI01, EM13CNT104, EM13CNT103
Sugestão:
1. Observe que há uma barra deslizadora no topo do objeto; arraste-a para observar velocidades distintas para a animação;
2. Observe que a imagem foi possibilitada por "zoom" no ecrã gráfico, para melhorar a visualização dos planetas. Nesse sentido, experimente utilizar tal recurso durante a animação;
2. Veja que existem 8 planetas na animação, não se inserindo o planeta-anão Plutão. Isso não é por descaso ao próprio, mas porque você pode observar o quão lento é a movimentação dos planetas a medida que se distanciam do Sol (vide Netuno, praticamente estático). Nesse sentido, verifica-se o potencial de uma animação com dados aproximados, trazendo consigo informações adicionais não perceptíveis nos livros-texto sobre o assunto.
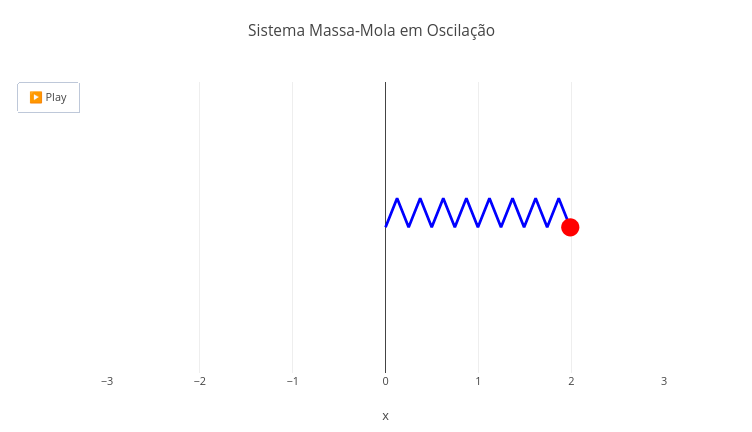
4.6 Movimento harmônico simples (Física)
BNCC: EF09CI09, EF09MA18, EM13CNT104, EM13CNT203
Equação
\[
x(t)=Acos(ωt+ϕ)
\]
Onde:
- x(t) = A posição da massa no tempo t;
- A = amplitude do movimento, que é a distância máxima da massa a partir da posição de equilíbrio (no caso, x=0);
- \(\omega\) = frequência angular, que define a taxa de oscilação. Ela é calculada por 2\(\pi\)/T, onde T é o período (o tempo para um ciclo completo);
- \(\phi\) = fase inicial ou constante de fase, que define a posição da massa em t=0
Sugestão:
1. Experimente alterar alguns parâmetros da equação de movimento, como a amplitude A e a frequência angular;
2. Aumente a frequência angular da animação reduzindo o denominador em "const w";
2. Experimente o botão "html" e evidencie que a animação é preservada na exportação do arquivo;
3. Experimente o botão "clone" e evidencie que é possível compartilhar o objeto na configuração congelada juntamente ao código modificado
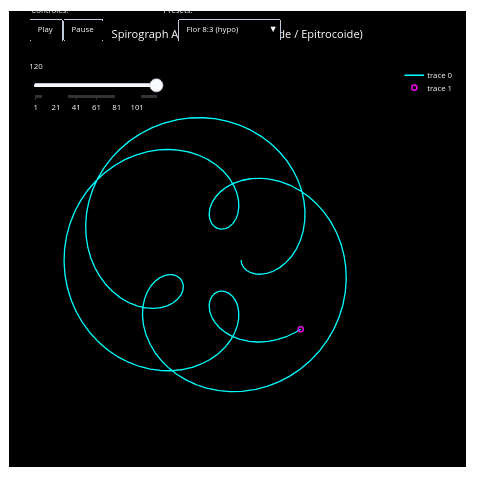
4.7 Espirógrafo animado
BNCC: EF07MA18, EF09MA20, EM13MAT406, EM13LGG701)
Sugestão:
1. O objeto permite alterar o tipo de hipo ou hipertrocoide por menu, assim como pausar a animação por botão;
2. É possível alterar o padrão trocoide das figuras modificando-se uma relação matemática. Exemplificando, procure no código pela linha "Math.cos(t) + d*Math.cos(k1*t);", e altere o segundo termo para "Math.sin"
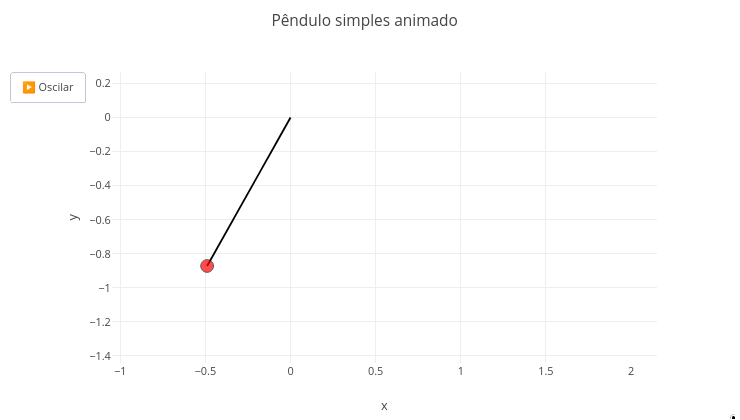
4.8 Movimento pendular (Física)
BNCC: EF09CI09, EF09MA18, EM13CNT104, EM13CNT203
Equação
\[ θ(t)=θ_0cos(ωt) \]
\[ x(t)=Lsin(θ) \]
\[ y(t)=−Lcos(θ) \]
\[ ω=\sqrt{\frac{L}{g}} \]
Onde:,
- θ(t) = posição angular;
- x(t) = coordenada x;
- y(t) = coordenada y;
- ω = frequência angular
Sugestão:
1. Como sugerido para outros objetos, experimente a "exploração paramétrica" da equação envolvida no código, alterando seus parâmetros;
2. Observe uma característica vantajosa de simulações sobre experimentos reais: a realização em condições impossíveis na prática. Para isso, experimente a simulação como se estivesse na Lua, com alteração no valor de aceleração da gravidade para 1,62 m/s^2 (mas com ".", e não "," - por tratar-se de sintaxe de programação.
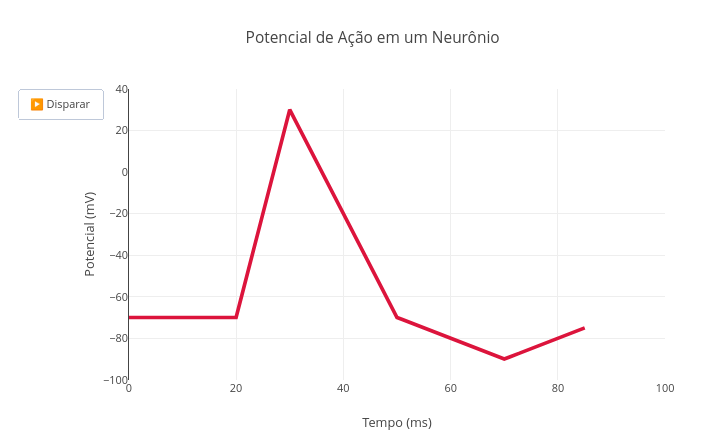
4.9 Potencial de ação em neurônio (Biologia)
BNCC: EF08CI08, EF09CI01, EM13CNT202, EM13CNT302
Sugestão:
1. Experimente alterar os valores padrão para os potenciais apresentados em "function potencial(i)" do código;
2. Valores alterados estão presentes em alguns quadros neurológicos, como epilepsia e esclerose múltipla.
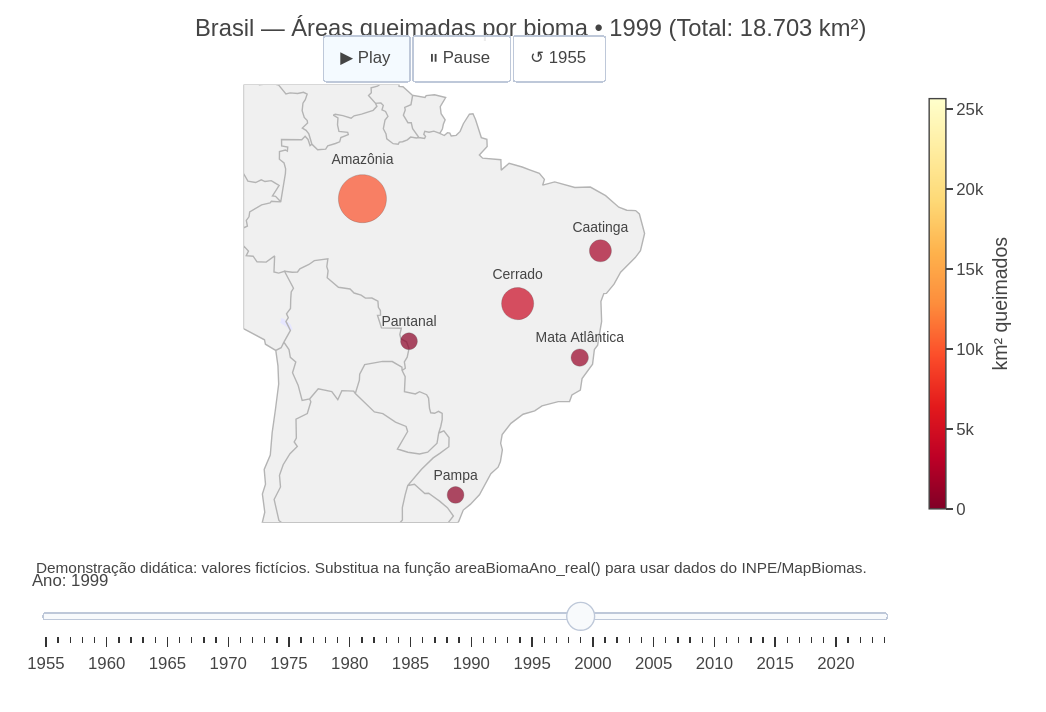
4.10 Mapa de áreas queimadas por biomas no Brasil
BNCC: EF07CI08, EF08GE08, EM13CHS101, EM13CNT201
1. É salutar buscar fontes de informação mais precisas sobre os temas tratados, posto que o GSPlotly, como um assistente de IA, não garante a a natureza das informações. No exemplo, sugere-se o "Programa Queimadas - INPE - Terrabrasilis" (https://terrabrasilis.dpi.inpe.br/queimadas/situacao-atual/situacao_atual/);
2. Pode-se inserir dados mais precisos no próprio script, no campo de "const usar_dados_ficticios = true; // mude para false e preencha areaBiomaAno_real()";
3. Pode-se modificar a temática do mapa animado para qualquer outra, bastando-se alterar os dados nas constantes de "Controle Geral" do script.
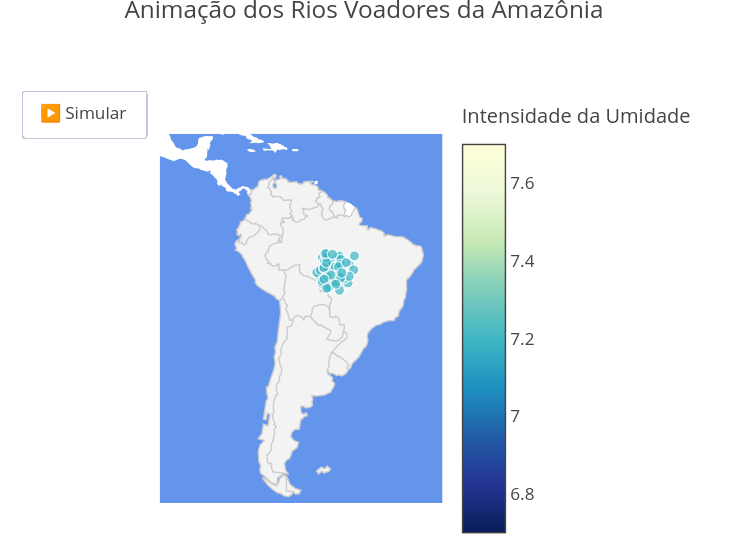
4.11 Deslocamente de rios voadores (Ciências Ambientais)
Sugestão:
1. Simule o efeito de desmatamento reduzindo o fator empírico associado: "const desmatamento_fator = 0.01";
2. Simule um aumento da umidade na animação: "const n_particulas = 1000";
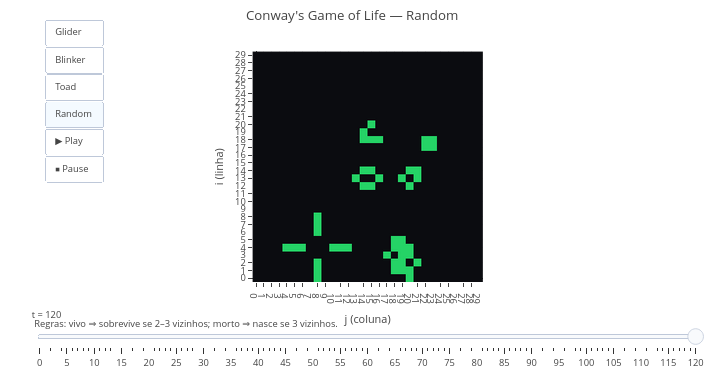
3. Aumente a dispersão do volume de água: " const x_final = x_inicial + (i / nFrames) * (Math.random() * 50 + 10);"4.12 Jogo da Vida de Conway
BNCC: EF06MA20, EF09MA24, EM13MAT503, EM13CNT201
Sugestão:
1. Veja no topo do código que é possível alterar-se o tamanho da grade, os passos de tempo, e a probabilidade de uma célula estar viva no modo "Random".
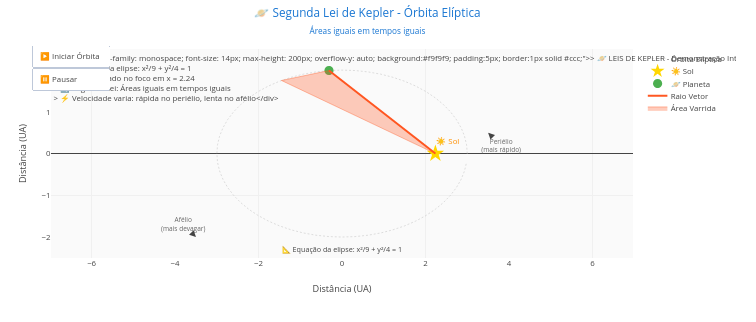
4.13 Segunda Lei de Kepler (Física)
BNCC: EM13CNT101, EM13CNT201, EM13CNT204, EM13CNT206
Equação:
\[ c=\sqrt{a^2+b^2} \] | A posição do planeta é calculada ao longo do tempo por meio das equações paramétricas da elipse, e a animação evidencia a variação da velocidade orbital: maior no periélio e menor no afélio. O parâmetro N controla a resolução temporal da animação, enquanto o incremento dt permite visualizar, a cada passo, a área varrida pelo raio vetor Sol–planeta.
Sugestão:
1. Observe que, embora o planeta percorra distâncias diferentes em intervalos de tempo iguais, a área varrida permanece constante, traduzindo de forma intuitiva a conservação do momento angular no movimento orbital. Isso significa que a velocidade do planeta varia, sendo mais rápido no periélio (perto do Sol) e mais lento no afélio (longe);
2. Experimente rodar a simulação variando os eixos "a" e "b" para a Terra. Uma aproximação sugerida: 299200000 (eixo maior) e 299158000 (eixo menor) km. Se não observar nada, clique em "Autoscale" na barra superior;
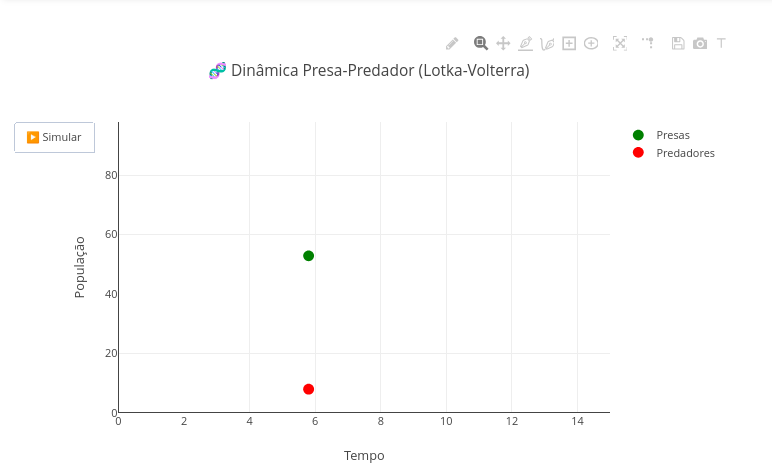
3. Veja que a diferença é de apenas 21 mil km, significando a órbita da Terra é 99,98 % "circular", embora o Sol esteja deslocado do centro.4.14 Modelo Presa-Predador (Biologia)
BNCC: EM13CNT101, EM13CNT201, EM13CNT204
Equação:
\[
\frac{dx}{dt} = \alpha x - \beta x y
\]
\[
\frac{dy}{dt} = \delta x y - \gamma y
\]
Onde:
- \(\alpha\) = taxa de crescimento das presas;
- \(\beta\) = taxa de predação por encontro presa–predador;
- \(\delta\) = eficiência de conversão/produção de predadores a partir da predação;
- \(\gamma\) = taxa de mortalidade dos predadores.
Sugestão:
1. Altere alguns parâmetros do script isoladamente, e observe os efeitos na animação:
a. N: no. de pontos (tempo da simulação)
b. Populações iniciais de presas e predadores (x e y);
2. Experimente alterar a taxa de predadores para um valor extremo: "const delta = 0.1"5 Simulações
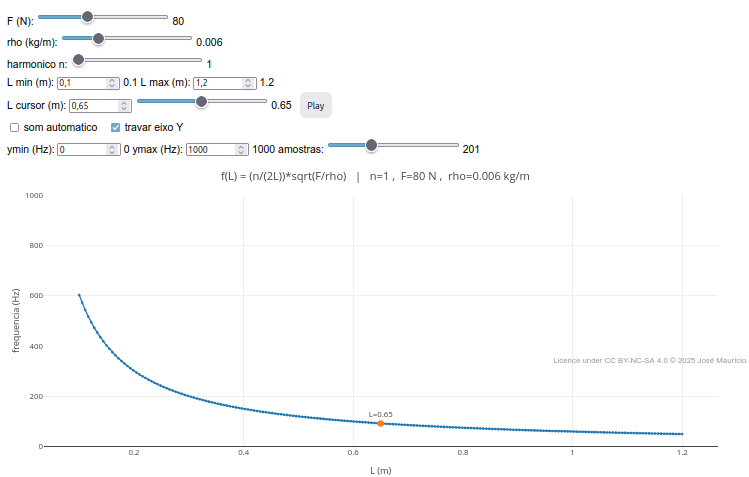
5.1 Corda vibrante & sons
BNCC: EM13CNT101, EM13CNT203, EM13CNT204, EM13CNT206
tone.js para reprodução sonora do efeito verificado. Isso permite ouvir a frequência correspondente, reforçando a conexão entre o modelo físico, a representação matemática e a percepção auditiva.- A tração controla a energia mecânica armazenada na corda;
- A densidade linear representa a inércia do sistema;
- O comprimento define as condições de contorno;
- O modo harmônico determina o padrão espacial da onda;
- A frequência audível conecta o modelo físico à percepção sonora.
Equação:
Velocidade da onda na corda
\[ v = \sqrt{\frac{F}{\rho}} \]
onde:
- é a velocidade da onda (m·s(^{-1}));
- é a tração aplicada à corda (N);
- () é a densidade linear de massa da corda (kg·m(^{-1})).
Frequência dos modos normais de vibração
\[ f_n = \frac{n}{2L}, v \]
\[ f_n = \frac{n}{2L}\sqrt{\frac{F}{\rho}} \]
onde:
- (f_n) é a frequência do harmônico (n) (Hz);
- é o número do modo harmônico ((n = 1, 2, 3, ));
- é o comprimento vibrante da corda (m);
- é a tração (N);
- () é a densidade linear (kg·m(^{-1})).
Dependência funcional da frequência com o comprimento
\[ f(L) \propto \frac{1}{L} \]
Comprimento de onda dos harmônicos
\[ \lambda_n = \frac{2L}{n} \]
onde (_n) é o comprimento de onda do harmônico (n).
5.1.1 Relação fundamental entre frequência, velocidade e comprimento de onda
\[ f_n = \frac{v}{\lambda_n} \]
Sugestão:
1. Observe a variação de comprimento da corda em "L" no gráfico quando se arrasta algum slide;
2. Experimente clicar no checkbox "som automático", e arraste algum slider;
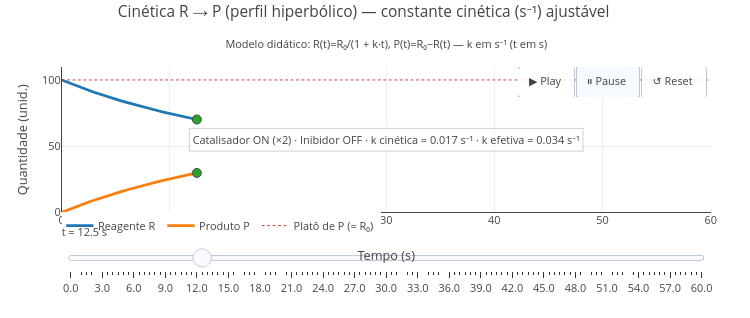
3. Observe o efeito quando se altera alguns dos parâmetros nos sliders, como "F", "rho", e "harmonico";5.2 Cinética de reação química
BNCC: EF09CI07, EM13CNT204, EM13CNT205
Equação:
\[ R(t)=\frac{R_0}{1+k_{efetiva}t} \]
\[ P(t)=R_0−R(t) \]
Onde,
- \(R(t)\) = quantidade de reagente R no instante \(t\) (unidades arbitrárias);
- \(P(t)\) = quantidade de produto P no instante \(t\) (unidades arbitrárias);
- \(R_{0}\) = quantidade inicial de reagente no tempo \(t=0\);
- \(t\) = tempo (em segundos);
- \(k_{\text{cinética}}\) = constante de velocidade de base (em \(s^{-1}\));
- \(k_{\text{efetiva}}\) = constante efetiva após considerar catalisador e/ou inibidor:
\[ k_{\text{efetiva}} \;=\; k_{\text{cinética}} \times \begin{cases} f_{\text{cat}}, & \text{se catalisador ligado}\\[6pt] 1, & \text{se catalisador desligado} \end{cases} \times \begin{cases} \dfrac{1}{f_{\text{inh}}}, & \text{se inibidor ligado}\\[6pt] 1, & \text{se inibidor desligado} \end{cases} \]
Sugestão
1. Experimente alterar a constante "k_cinetica" no topo do código (ex.: 0.008, 0.017, 0.05) e use Play/Reset para comparar;
2. Experimente incluir/retirar inibidor e catalisador;
3. Experimente alterar o potencial dos moduladores acima editando suas constantes:
a. const fator_catalise = 2.0;
b. const fator_inibicao = 3.0;
6 Aplicativos
6.1 Prancha de desenho
BNCC: EF15AR06, EF09AR07, EM13LGG604, EM13LGG606
Sugestão
1. Explore o script. Apesar de simples, ele permite selecionar cores distintas, espessuras de canetas, e formas geométricas;
2. Como os demais objetos elaborados no JSPlotly, o desenho da prancha pode ser armazendo conservando sua interatividade pelo botão "html", e mesmo modificado no próprio arquivo salvo ("play.html");
3. Se desejar alterar cores, espessuras, ou quiser acrescentar outras funcionalidades, verifique as variáveis do script;
4. Experimente o botão "clone", que permite clonar a prancha juntamente com seu código.
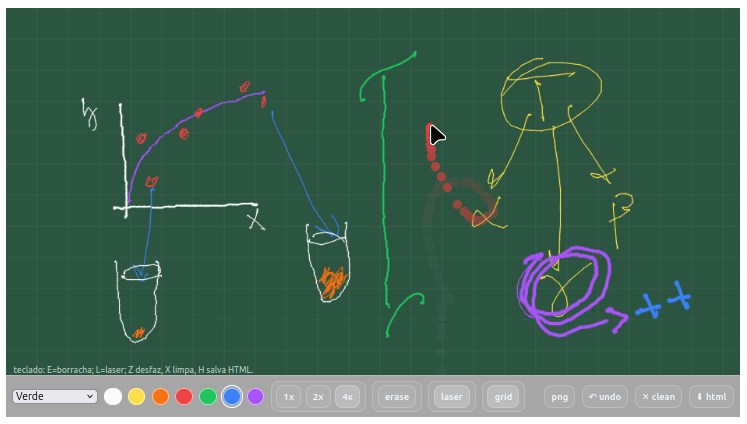
6.2 Gizz - Lousa Digital
- Pode ser exportada como arquivo autossuficiente HTML em botão da própria lousa, e permitindo compartilhamento da imagem gerada, bem como continuidade de sua edição;
- Faculta a personalização do código que o produz, permitindo inserir/alterar canetas, espessuras, e ações distintas não previstas no código-fonte.
- Escrever com 7 cores e 3 espessuras distintas;
- Acessar 4 planos de fundo de coloração diferente;
- Sobrepor o plano com um grid;
- Utilizar um apagador (erase);
- Utilizar um apontador de laser para localização do que se pretende assinalar;
- Salvar a imagem como PNG, indicando data e hora;
- Salvar a imagem como HTML autossuficiente (obs: botão html do quadro; o do editor não funciona neste objeto);
- Comando de desfazer (undo) e de limpeza (clean) do quadro;
- Possui atalhos de teclado: E=borracha; L=laser; Z desfaz, X limpa, H salva HTML
Sugestão:
1. Pode-se alterar a espessura das canetas em "var baseWidth = 1;" ;
2. Os botões 1x, 2x, 4x são multiplicadores; edite as linhas de criação dos botões pra trocar rótulo/multiplicador (ex.: "addSize('3x', 3, true)").
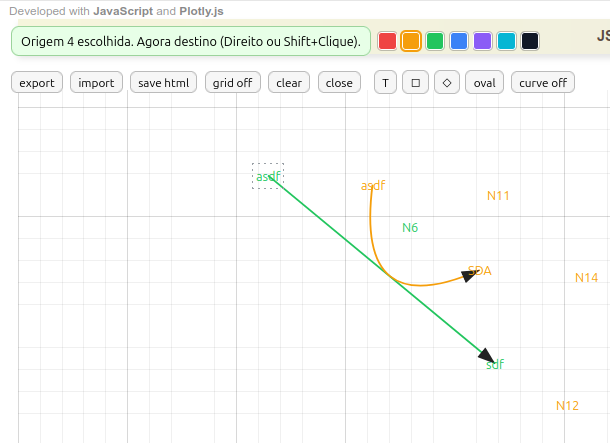
Obs: o botão funcional para reprodução do quadro é o que está na própria lousa, "html". O botão do editor de códigos não opera para o aplicativo.6.3 MentMapa - editor para mapa mental e diagramas
Instruções para o MentMap
- Criação de termos. Clique com o botão esquerdo do mouse e digite um termo; clique em Esc para sair;
- Deleção de termos. Clique Ctrl+botão direito do mouse;
- Moldura nos termos. Clique numa moldura da barra (quadrado, losango, oval);
- Ligação de termos por seta. Clique com o botão direito do mouse no 1o. termo, seguido do botão direito no 2o. termo;
- Seta curva. Clique em curve on. Depois, clique com o botão direito do mouse no 1o. termo, seguido de clique com botão esquerdo em um ponto entre os dois termos, e finalize com o botão direito no 2o. termo. Para acertar a curvatura da seta, clique na bolinha e arraste-a para encostar num termo ou numa seta;
- Arraste de termos e setas. Basta clicar e arrastar.
- Arraste de um grupo de termos/setas. Clique em Shift e desenhe a área que se deseja abarcar o grupo com o botão esquerdo do mouse;
- Cores para termos e setas. Selecione uma das 7 cores disponíveis na barra superior, e clique num termo já existente, ou novo. Obs: a cor da seta acompanha a dos termos;
- Grid para posicionamento mais preciso. Basta clicar em grid on (não fica salvo do diagrama final);
- Salvamento do mapa (save html). Diferente do botão html usual, o armazenamento do mapa interativo é realizado por um botão html próprio, na barra de ícones;
- Importação de mapas (import). O aplicativo permite importar um mapa já pronto em formato json para continuar sua edição;
- Exportação de mapas (export). O aplicativo também permite exportar o mapa no formato json para estudo futuro ou simples guarda.
Sugestão:
1. O editor permite criar mapas mentais, diagramas, fluxogramas, e outras representações...então agora a sugestão é vossa !!
7 Jogos
7.1 Jogo de Memória
BNCC: EF06MA19, EF06MA16, EF07MA26, EF09MA19, EM13MAT401, EM13MAT102, EM13MAT403, EM13LGG701
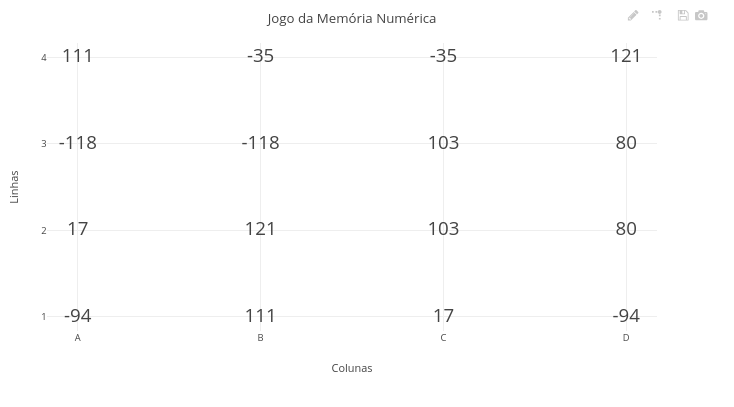
Instruções para o Jogo de Memória Numérica:
- No campo superior existem duas constantes booleanas true/false, uma para jogar (jogue) e outra para verificar o acerto (verificar), bem como uma semente que fixa um determinado quadro numérico aleatório;
- Inicie o jogo (jogue/false, verificar/false);
- Clique no botão add e será exibido um quadro de pares numéricos para memorização;
- Troque para jogue/true, clique em clean plot, e depois em add. O quadro será exibido agora apenas com um valor (demais células mostratrão “?”);
- Escolha verificar/true, clique em clean plot, e depois em add. Será apresentado um campo para se digitar as coordenadas em que se acredita estar o outro par numérico (Ex: A2);
- Clique em OK, e será apresentado um par formado pelo valor inicial e o valor escolhido, para verificação do acerto.
1. Para jogar novamente alterando os valores do quadro, basta modificar a constante *semente* para um número qualquer;
2. Para variar entre níveis de dificuldade do jogo, basta alterar o número de linhas e de colunas nas constantes respectivas do código.
8 Acessibilidade e inclusão
8.1 Equasons
BNCC: EF69LP27, EF69AR09, EM13MAT406, EM13LGG604, EM13LGG701
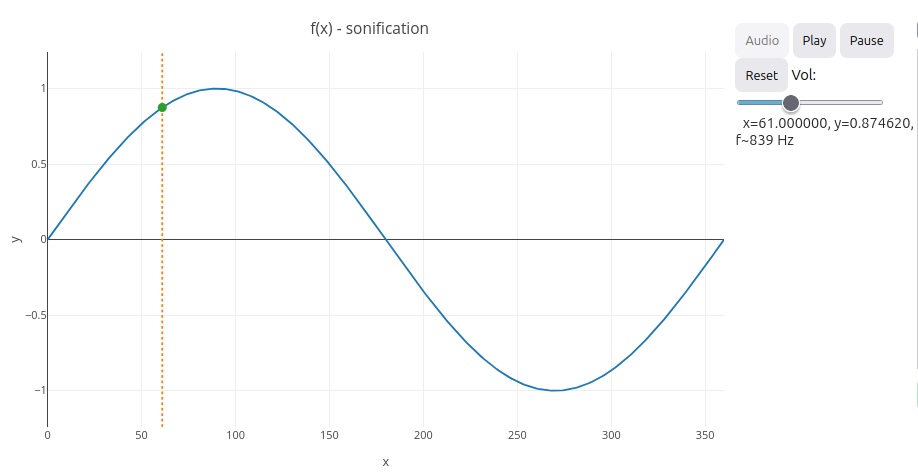
Sugestão:
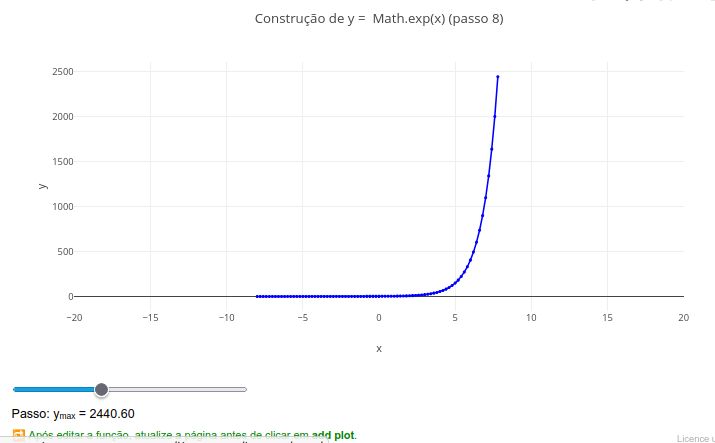
1. Pode-se editar o código para uma função específica. Para isso, basta mudar a linha "var f = function(x){ ... }". Exemplos:
a. return Math.sin(x*Math.PI/180); (graus);
b. return Math.sin(x); (radianos);
c. return Math.exp(-0.01*x)*Math.cos(0.2*x);
2. Pode-se alterar a velocidade de deslocamento da função pela função abaixo, e cujo valor é dado em milisegundos:
"var PLAY_INTERVAL_MS = 100; "
9 Musicalização
9.1 FlautaDoce
BNCC: EF15AR05, EF69AR09, EM13LGG601, EM13LGG604, EM13LGG701
Sugestão
1. A flauta foi concebida para tons (círculo) e semitons (semicírculos). Você pode "tocar" a flauta clicando com o botão esquerdo do mouse sobre um orifício ou utilizando o dedo em um smartphone;
2. Você pode acrescentar ou omitir algum orifício na flauta, bastando alterar as duas linhas das variáveis "var naturais" e "var sustenidos";
2. Você pode transformar sua flauta num "pífano", geralmente mais agudo que a flauta doce, e bastante comum da tradição nordestina. Para isso, basta substituir as linhas das variáveis "var naturais" e "var sustenidos", mudando o valor de "5" para "6", como segue (adicione "add" em seguida - ou "clean"/"add"):
var naturais = ["C6","D6","E6","F6","G6","A6","B6"];
var sustenidos = ["C#6","D#6","F6","F#6","G#6","A#6","B6"];
3. Na linha de raciocício acima, também é possível mudar o padrão da flauta doce, flautas baixas e contra-baixo. Exemplificando, uma flauta germânica (orifício maior, soprano, utilizada nas Escolas e representada no script) ou barroca (orifício menor, tons mais graves).
9.2 Piano
BNCC: F15AR05, EF69AR09, EM13LGG601, EM13LGG604, EM13LGG701
Sugestão
1. É um piano pequeno, mas é um piano (2 oitavas) !! E como tal, você pode expressar sua aptidão musical com o instrumento polifônico;
2. Para prolongar o som das teclas eleve a barra de "sustentação";
3. Como parte do JSPlotly, o piano pode ser compartilhado sem o código, somente como instrumento para musicalização ou treino, já que é exportado pelo botão "html", preservando sua interatividade e sonorização por mouse ou toque de dedos num dispostivo móvel;
4. Também como parte do JSPlotly, é possível compartilhar o piano com os códigos para alteração junto ao botão "clone";
10 Games
10.1 Jogo de Arco e Flecha
BNCC: EF09CI09, EF09MA18, EM13MAT302, EM13CNT104, EM13LGG701
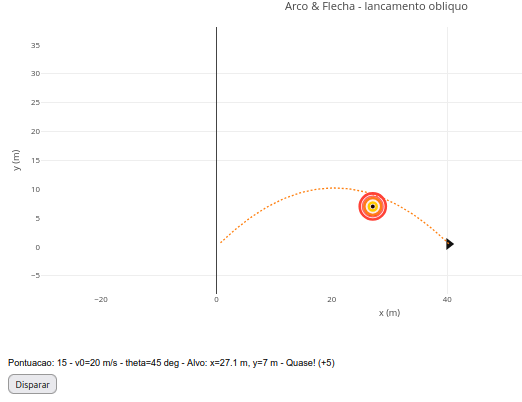
Sugestão
1. Altere o ângulo ("let theta_edit = 45") e/ou a velocidade inicial do disparo ("let v0_edit = 20") para ajustar a parábola ao alvo;
2. Perceba que a pontuação é flexível: 5 pontos para proximidade do alvo, e 10 pontos quando o acerta.
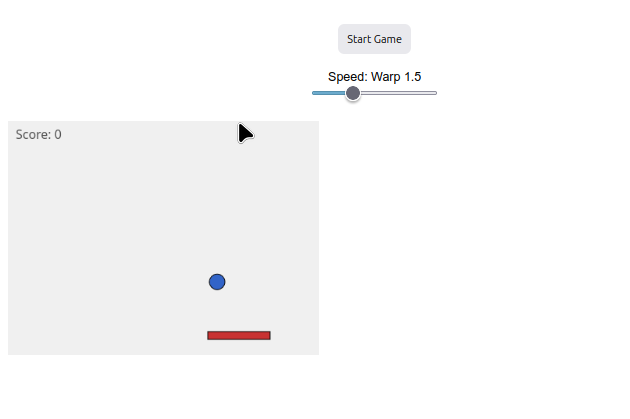
10.2 Game Pong
BNCC: EF69AR09, EF06MA20, EM13LGG604, EM13LGG701
Sugestão:
1. Se achar que o jogo está lento, mesmo na velocidade 'warp' máxima, é possível alterar seu valor em "var base = Math.pow(1.5, warp);";
2. Se achar que o jogo tá difícil ou fácil demais, é possível alterar o tamanho da raquete em "paddle = { w: 80, h: 10,...";
3. Se desejar aumentar a área do jogo, modifique na linha abaixo (largura, altura):
"var cv = sk.createCanvas(400, 300).parent('jogoArea');"
11 Interface Experimental
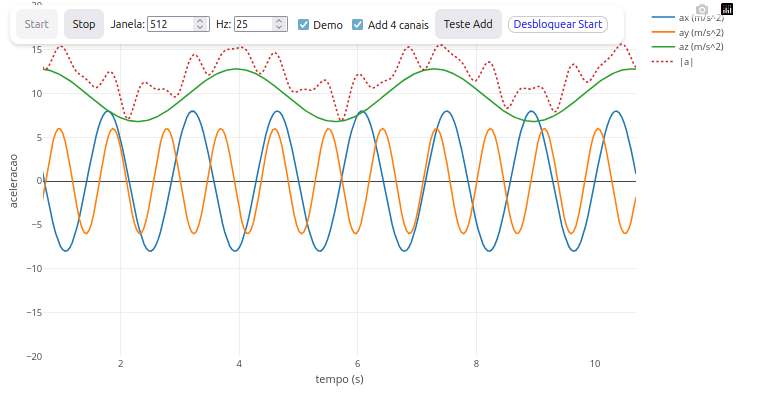
11.1 Celular - Aquisição de dados de sensores
Sugestão:
1. Como o aplicativo é para o posicionamento "x, y e z" de um dispositivo móvel, experimente alterar a posição de seu celular/tablet no espaço.11.2 Arduino - Aquisição de dados de condutivimetria
BNCC: EM13CNT201, EM13CNT308, M13CNT301, M13CNT302
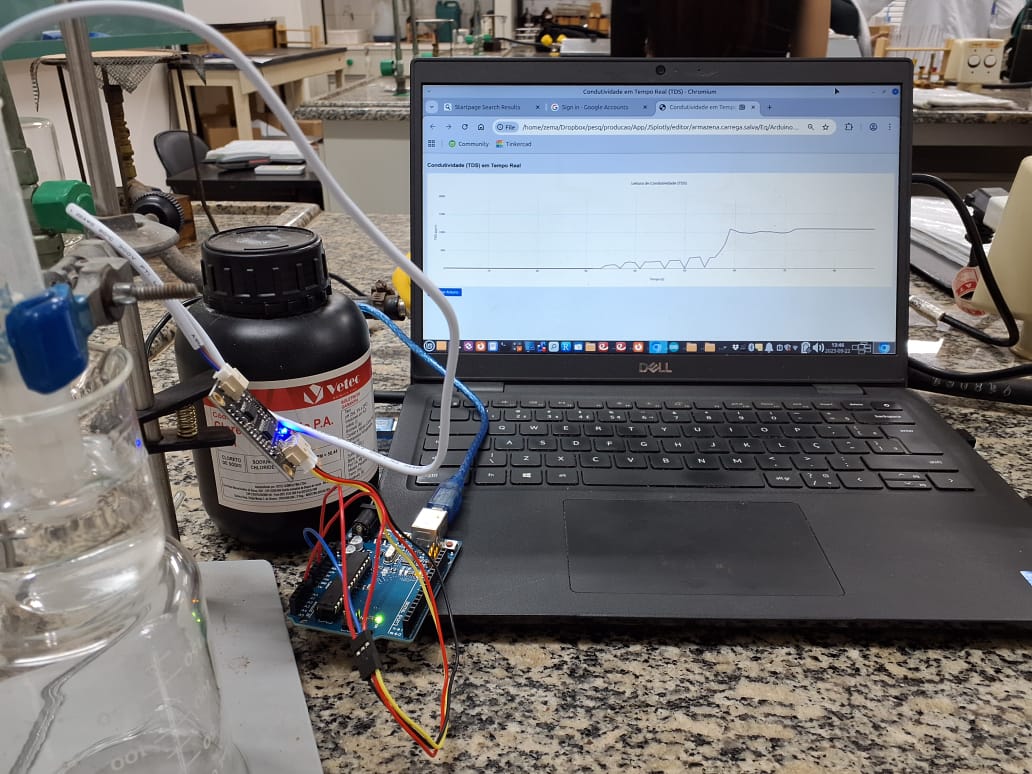 Exemplo de aplicação de JSPlotly para interfaceamente com Arduino. O gráfico apresenta medidas de condutividade em meio aquoso com medidor TDS para teores crescentes de NaCl (sonda no canto esquerdo). Clique na imagem para obter o aplicativo JSPlotly autônomo para condutividade.
Exemplo de aplicação de JSPlotly para interfaceamente com Arduino. O gráfico apresenta medidas de condutividade em meio aquoso com medidor TDS para teores crescentes de NaCl (sonda no canto esquerdo). Clique na imagem para obter o aplicativo JSPlotly autônomo para condutividade.
Instruções:
- Para conexão Web Serial é necessário instalação de Python ao computador (Windows ou Linux), e setup de servidor local. Para Windows baixe e instale o arquivo oficial para Python, lembrando-se de clicar em Add Python to PATH, e digite os comandos no CMD dentro da pasta do aplicativo autônomo. Segue a orientação para Linux:
- Conecte o Arduino e componentes (sonda TDS, recipiente com água e sal);
- Feche a IDE do Arduíno;
- Abra um Terminal na pasta do aplicativo autônomo do JSPlotly para Arduino (condutiv_JSPlotly.html);
- Digite: python3 -m http.server
- Abra o html autônomo do circuito no Chrome (nunca no Firefox);
Sugestão:
1. Como o aplicativo é escrito no JSPlotly, é possível personalizá-lo para diversas situações, como taxa de tranferência de dados, traços (tipo, cores, espessura), tipo de gráfico, entre outros.