Simulações Interativas com JSPlotly

Para ilustrarrr o potencial de uso do JSPlotly para Bioquímica e áreas correlatas, seguem alguns exemplos para gráficos, simulações, análise de dados, e aplicativos, e cujos conteúdos são frequentemente encontrados em livros-texto e fontes técnico-científicas. Para um melhor aproveitamento de cada tema, experimente seguir as Sugestão dos códigos para cada objeto.

1 Simulações

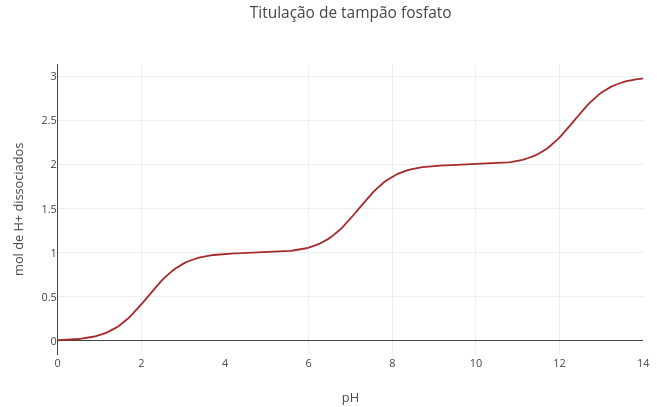
1.1 Equilíbrio ácido-básico e sistema tampão

Contexto:

O exemplo ilustra a adição de base num sistema contendo um ácido fraco e sua base conjugada. A equação de titulação refere-se a um ácido triprótico, o ácido fosfórico do tampão homônimo, mas serviria igualmente para outros tantos, como os presentes no ciclo de Krebs (citrato, isocitrato).

Equação:

\[ fa= \frac{1}{1 + 10^{pKa1 - pH}} + \frac{1}{1 + 10^{pKa2 - pH}} + \frac{1}{1 + 10^{pKa3 - pH}} \]

Onde, fa = fração de ácido (grupos protonáveis)

Sugestão:

"A. Convertendo a curva de tampão fosfato (triprótico) para tampão bicarbonato (diprótico)"

1. Altere os valores de pKa para o tampão bicarbonato: pKa1 =      6.1, e pKa2 = 10.3;
2. Coloque um valor muito grande para pKa3 (ex:1e20).
3. Clique em "add plot".

Explicação: pKa é um termo que representa o logaritmo de uma constante de dissociação (-log[Ka]). Com um valor extremo, o denominador torna-se igualmente imenso, anulando o termo que leva pKa3. Em JavaScript e outras linguagens, "e" representa a notação para potência de 10.

"B. Convertendo a curva de tampão bicarbonato para acetato"

1. Basta repetir o procedimento acima, com pKa1 = 4.75, e eliminando-se pKa2.

1.2 Estado de ionização de grupos químicos de biomoléculas

Contexto:

O JSPlotly também permite a observação de alguns conceitos facilitados por aprendizagem baseada em animação junto às representações gráficas obtidas por funções matemáticas. No exemplo que segue, o objeto interativo ilustra o estado de protonação para os principais grupos químicos encontrados em biomoléculas.

Instrução

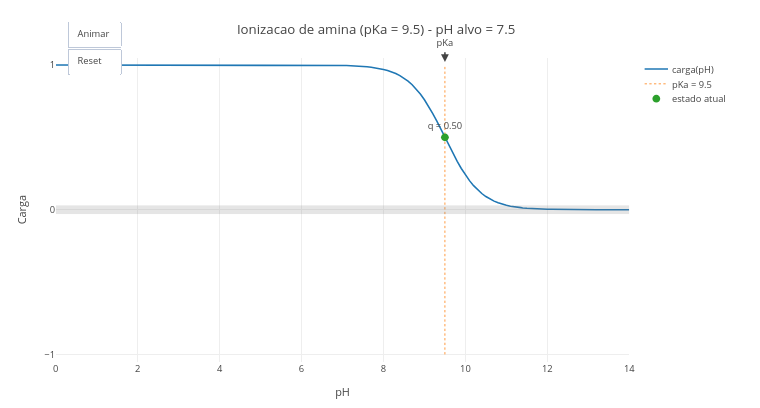
Após clicar na imagem correlata abaixo, clique em “add” e observe o gráfico de titulação ácido-basica gerado. O eixo das abscissas (eixo x) possui uma faixa extensa de valores de pH, e o eixo das ordenadas a carga que a molécula com potencial de ionização se manifesta em cada pH, e em função de seu valor de pKa;
Clique em “Animar” para observar o deslocamento de uma bolinha ao longo da curva de titulação, até um valor de pH pré-definido no script do simulador, e em função de seu pKa;
Modifique no script o tipo de grupo ionizável (em “let grupo_edit =”) e/ou o pH final desejado (“let pH_final_edit =”), para avaliar o estado de ionização de um novo grupo;
Clique em “Reset” e “Animar”, para observar a nova animação.

Sugestão:

1. Troque o pH e o tipo de grupo que se pretende observar;
2. Simule o estado de ionização de moléculas diferentes, como fármacos com ácido carboxílico (ex: ácido acetilsalicílico...aspirina), no pH sanguíneo e na cavidade gástrica;
3. Crie um novo grupo ionizável e preveja seu estado de ionização. Para isso, basta alterar a informação em 3 constantes ao início do script: grupos, pKas, e tipos.
  a.

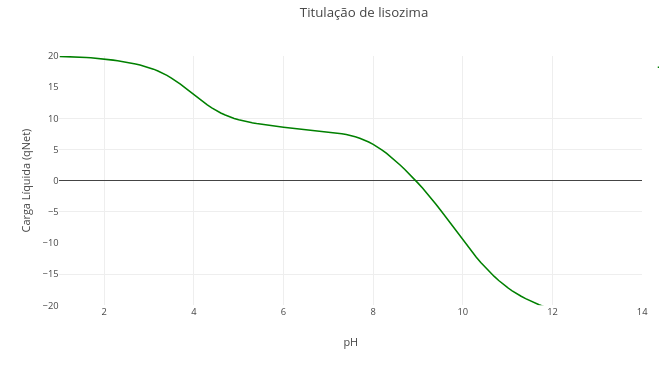
1.3 Rede de carga líquida em peptídios

Contexto:

O código refere-se à rede de carga líquida presente numa sequência qualquer de resíduos de aminoácidos. Aqui é ilustrada a angiotensina II, importante peptídio para regulação da pressão arterial e equilíbrio eletrolítico, e cuja enzima conversora está associada ao mecanismo de invasibilidade celular por SARS-CoV-2.

Equação:

Para essa simulação não há uma equação direta, já que o algoritmo precisa decidir a carga em função da natureza básica ou ácido do resíduo em determinado valor de pH (observe o script). Assim:

\[ q = \begin{cases} -\dfrac{1}{1 + 10^{pK_a - pH}} & \text{(grupo ácido)} \\\\ \dfrac{1}{1 + 10^{pH - pK_a}} & \text{(grupo básico)} \end{cases} \]

Onde,

pKa = valor do antilogarítmo de base 10 para a constante de equilíbrio de dissociação do ácido, Ka (ou log[Ka]).

Sugestão:

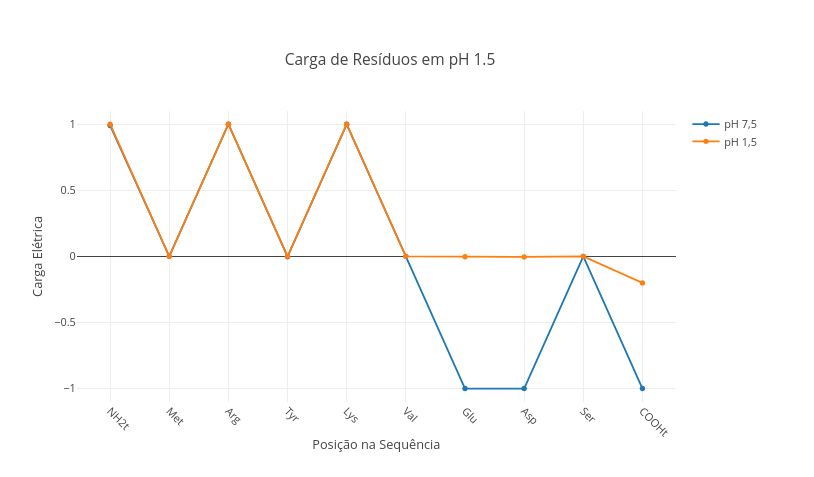
1. Selecione a sequência peptídica abaixo, e observe a distribuição de cargas:

"Ala,Lys,Arg,Leu,Phe,Glu,Cys,Asp,His"

2. Simule a condição de pH do estômago ("const pH = 1.5"), e verifique a alteração de cargas no peptídio.

3. Selecione um peptídio fisiológico (oxitocina, por ex), observe sua carga no sangue (pH 7.5), e reflita sobre seu potencial de interação eletrostática com componentes celulares.

"Cys,Tyr,Ile,Gln,Asn,Cys,Pro,Leu,Gly"  - oxitocina

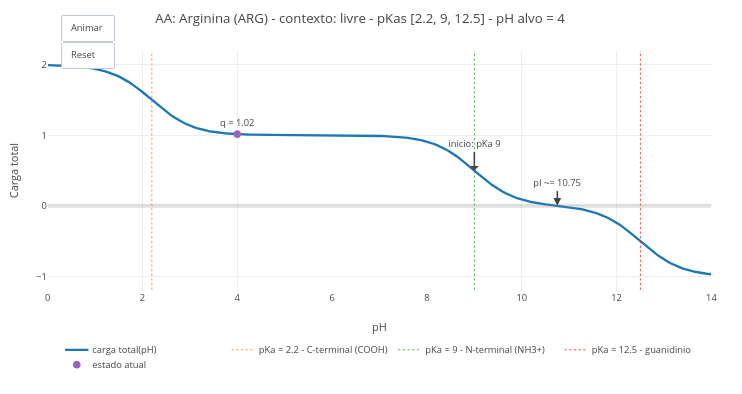
1.4 Carga, pH, pKa & pI de aminoácidos (animação)

Contexto:

Este objeto aborda um potencial diferente para o JSPlotly, qual seja, o aprendizado baseado em animação. Para ilustrar essa abordagem, segue uma animação para a observação de carga de um aminoácido baseada no valor de seu pKa, e na informação de seu pI, o ponto isoelétrico do composto (valor de pH em que a espécie possui carga líquida nula).

Para visualizar o valor da carga q (“estado atual”), clique no botão “add” seguido de “Animar”. Para outra animação, basta selecionar o aminoácido (“let aa_edit =”) e o pH final em que se deseja observar sua carga (“let pH_final_edit =”). A animação também permite compara a carga de um aminoácido livre com a do resíduo correspondente numa cadeia polipeptídica (opção “let contexto_edit =”). Observe que a animação fornece uma legenda informando o valor de pKa do composto para seus grupos ionizáveis.

Sugestão:

1. Simule a condição de um aminoácido no pH do sangue e no do estômago;
2. Compare os valores de pH de um aminoácido livre, com o de seu resíduo em cadeia;
3. Altere a opção booleana em "const showSites", para observar as curvas de cada grupo ionizável.

1.5 Ponto Isoelétrico em Proteínas

Contexto:

O script para esta simulação baseia-se na distribuição da rede de cargas para um polieletrólito, e a identificação do valor de pH em que essa rede é nula, ou seja o ponto isoelétrico (ou isoiônico), pI. O exemplo utiliza a sequência primária da lisozima, hidrolase que atua no rompimento da parede microbiana.

Equação:

\[ q_{\text{net}}(pH) = \sum_{i=1}^{N} \left[ n_i \cdot q_{B_i} + \frac{n_i}{1 + 10^{pH - pK_{a_i}}} \right] \]

Onde,

qnet = carga líquida total;
qB$_{i} = carga da forma básica para o resíduo i (por exemplo, +1 para Lys, 0 para Asp);
n$_{i}$ = número de grupos do resíduo i.

Sugestão:

"Descobrindo o pI para outras proteínas"

1. Pode-se verificar a titulação de qualquer outra proteína ou sequência peptídica por simples substituição da sequência primária contida no código. Uma forma ascertiva de realizar essa substituição envolve:
  a. Procurar a sequência "FASTA" da proteína no NCBI ("https://www.ncbi.nlm.nih.gov/protein/") - ex: "papain";
  b. Clicar em "FASTA" e copiar a sequência 1a. obtida;
  c. Colar a sequência num site para quantificação de resíduos (ex: "https://www.protpi.ch/Calculator/ProteinTool");
4. Substituir a sequência no código.

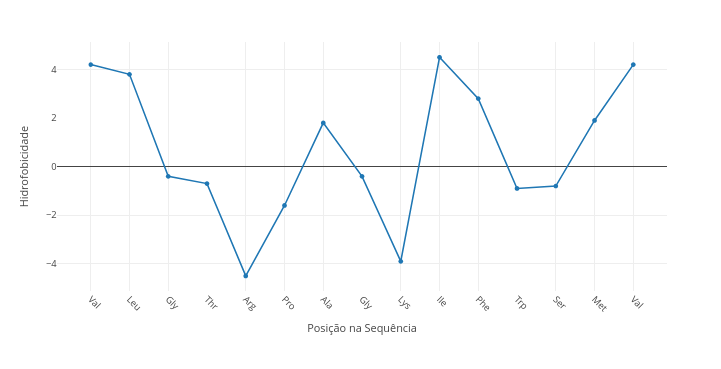
1.6 Hidrofobicidade em sequências de aminoácidos

Contexto:

A observação de níveis de hidrobicidade de aminoácidos pode ser de utilidade para o estudo e a predição de sequências de resíduos, tais como encontradas na porção central de hélices de proteínas transmembrânicas, como para identificação de sítios específicos em enzimas, como fendas e bolsões hidrofóbicos.

Esses níveis são classificados de modo relativos, dando origem a alguns índices como a escala de Kyte–Doolittle, que atribui a cada aminoácido um valor de hidropatia (hidrofobicidade/hidrofobicidade) estimado a partir de dados experimentais e observacionais. Valores positivos indicam tendência hidrofóbica (ex: Ile, Val, Leu) e valores negativos indicam tendência hidrofílica (ex: Asp, Glu, Lys, Arg). O índice permite destacar trechos propensos a ambientes não polares, bem como regiões expostas ao solvente aquoso.

Equação:

\[ \tilde{y}_i \;=\; \frac{1}{w} \sum_{k=i-m}^{i+m} y_k, \qquad w = 2m+1 \]

Onde,

\[\begin{aligned} y_i &:\; \text{valor de hidrofobicidade na posição $i$ da sequência} \\ \tilde{y}\_i &:\; \text{valor suavizado (média móvel) na posição $i$} \\ m &:\; \text{meia-janela (número de vizinhos de cada lado)} \\ w &:\; \text{largura total da janela ($w=2m+1$)} \\ i &:\; \text{posição do aminoácido na sequência ($1 \leq i \leq N$)} \end{aligned}\]

Sugestão:

1. Experimente trocar a sequência para uma conhecida;
2. Compare uma sequência polar com uma apolar por sobreposição ("add");
3. Transcreva uma sequência de hélice transmembrânica de uma proteína acessando seus dados pelo site PDB

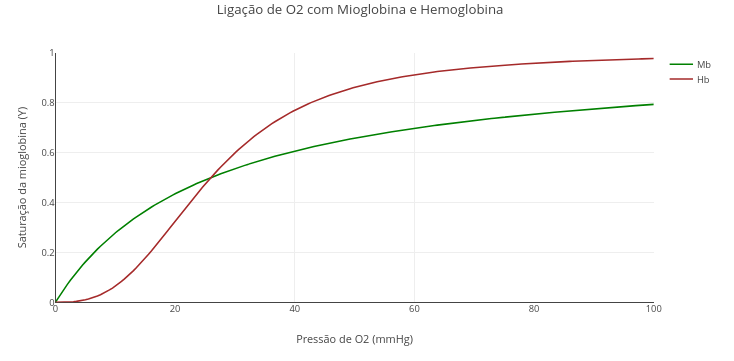
1.7 Interação de oxigênio com mioglobina e hemoglobina

Contexto:

A molécula de oxigênio pode combinar-se ao grupo heme de mioglobina e hemoglobina de forma distinta, em função da cooperatividade exibida nesta última frente à sua estrutura quaternária. O modelo que segue exemplica essa interação, por uso da equação de Hill.

Equação:

\[ Y= \frac{pO_2^{nH}}{p_{50}^{nH} + pO_2^{nH}} \]

Onde

Y = grau de saturação de oxigênio na proteína;
pO$_{2}$ = pressão de oxigênio;
p$_{50}$ = pressão de oxigênio a 50% de saturação;
nH = coeficiente de Hill para a interação;

Sugestão:

1. Rode o aplicativo ("add plot"). Veja que o valor de "nH" da constante de Hill é "1", ou seja, sem efeito de cooperatividade.

2. Agora substitua o valor de "nH" pelo coeficiente de Hill para a hemoglobina, 2.8, e rode novamente !

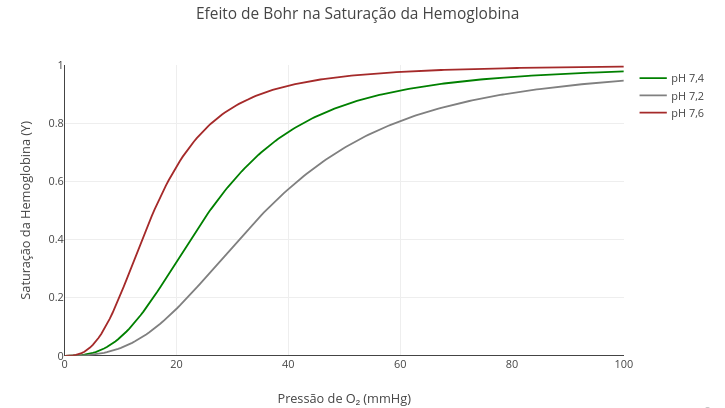
1.8 Efeito de Bohr em hemoglobina (pH)

Contexto:

Algumas condições fisiológicas ou patológicas podem alterar a afinidade de ligação do oxigênio com a hemoglobina, tais como a temperatura, alguns metabólitos (2,3-BPG), e o teor hidrogeneiônico da solução.

Equação:

\[ Y(pO_2) = \frac{{pO_2^n}}{{P_{50}^n + pO_2^n}}, \quad \text{com } P_{50} = P_{50,\text{ref}} + \alpha (pH_{\text{ref}} - pH) \]

Onde,

Y = saturação da hemoglobina,
pO$_{2}$ = pressão parcial de oxigênio (em mmHg),
P$_{50}$ = pressão de O$_{2}$ na qual a hemoglobina está 50% saturada,
P$_{50,ref}$ = 26 mmHg (valor padrão),
$\alpha$ = 50 (intensidade do efeito de Bohr),
pH$_{ref}$ = 7,4,
n = 2,8 = coeficiente de Hill para a hemoglobina.

Sugestão

1. Experimente alterar o pH de referência para a interação;
2. Simule outros modelos alostéricos alterando o valor de "n"

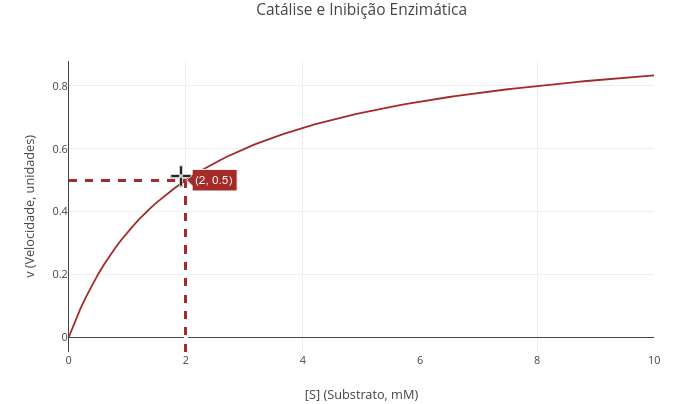
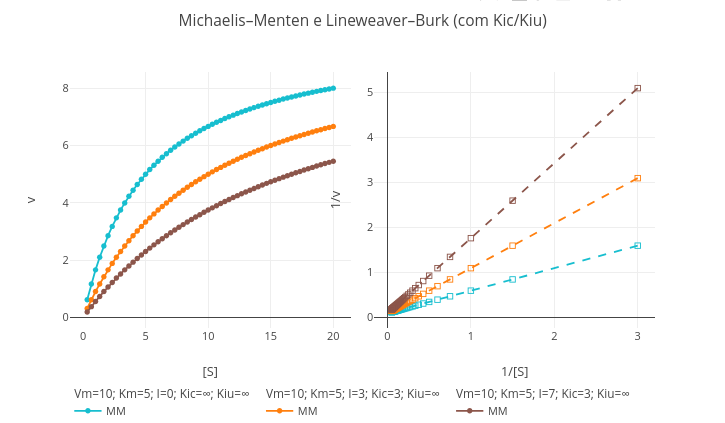
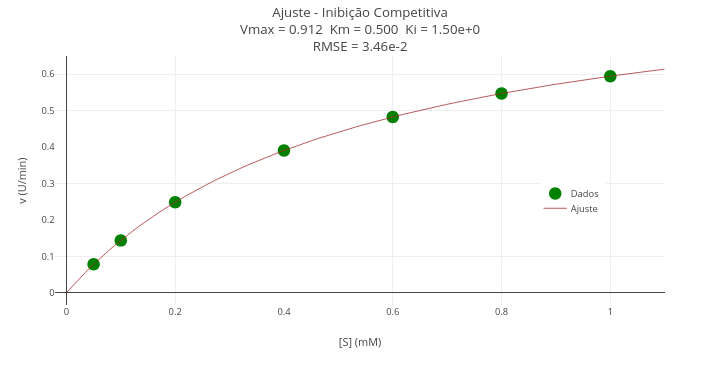
1.9 Catálise e inibição enzimática

Contexto:

A simulação que segue visa oferecer uma equação geral para estudos de inibição enzimática, que contemple os modelos competitivo, incompetitivo e competitivo (puro ou misto), também permitindo o estudo de catálise enzimática na ausência de inibidor.

Equação:

\[ v=\frac{Vm*S}{Km(1+\frac{I}{Kic})+S(1+\frac{I}{Kiu})} \]

Onde

S = teor de substrato para reação;
Vm = velocidade limite da reação (nos livros, velocidade máxima);
Km = constante de Michaelis-Mentem;
Kic = constante de equilíbrio de dissociação de inibidor para modelo competitivo;
Kiu = constante de equilíbrio de dissociação de inibidor para modelo incompetitivo

Sugestão:

"A. Catálise enzimática na ausência de inibidor."
1. Basta rodar o aplicativo com a equação geral. Veja que os valores para Kic e Kiu estão elevados (1e20). Dessa forma, com "constantes de dissociação" alta, a interação do inibidor com a enzima é irrelevante, retornando o modelo à equação clássica de Michaelis-Mentem.
2. Experimente alterar os valores de Vm e Km, comparando gráficos.
3. Use o recurso de coordenadas geográficas da barra de ícones ("Toggle Spike Lines"), para consolidar o significado matemático de Km, bem como observar o efeito de valores distintos desse sobre a visualização do gráfico.

"B. Modelo de inibição competitiva."
1. Para observar ou comparar o modelo michaeliano com o de inibição competitiva, basta substituir o valor de Kic para um número consistente (ex: Kic= 3).

"C. Modelo de inibição incompetitiva."
1. A mesma sugestão acima serve para o modelo incompetitivo, desta vez substituindo o valor para Kiu.

"D. Modelo de inibição não competitiva pura."
1. Neste modelo, a simulação dá-se por valores iguais para Kic e Kiu.

"E. Modelo de inibição não competitiva mista."
1. Para este modelo, basta alocar valores distintos para Kic e Kiu.

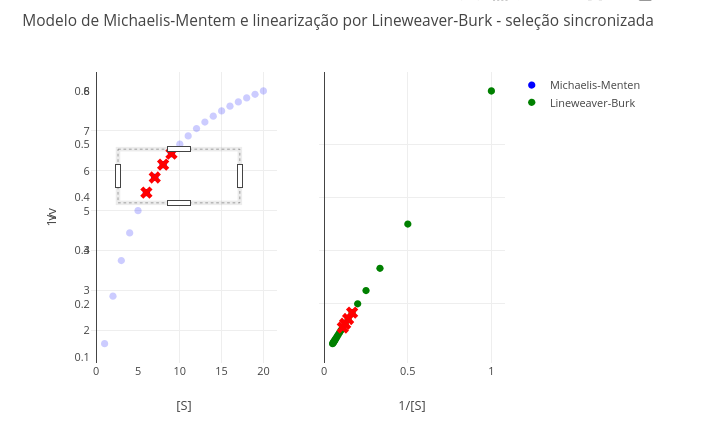
1.10 Linearização de dados cinéticos por Lineweaver-Burk

Contexto

Uma das (várias) dificuldades ao aprendizado em Bioquímica refere-se ao letramento para interpretação de gráficos. Entre esses, a natureza hiperbólica do modelo michaeliano é tratata alternativamente por diversas transformações das variáveis S e v, destacando-se na literatura a linearização por duplo-recíproco, ou transformação de Lineweaver-Burk.

O exemplo que segue ilustra a relação entre as variáveis dependente e independente do modelo original e transformado, utilizando-se outro recurso da biblioteca Plotly.js: a possibilidade de seleção cruzada de pontos.

Para observar essa funcionalidade, selecione um conjunto de pontos em um dos subplots do gráfico que segue, e observe sua seleção automática no outro subplot.

1.10.1 Equação

A transformação linear de Lineweaver-Burk é dada abaixo:

\[ \frac{1}{v} = \frac{1}{S}*\frac{Km}{Vm} + \frac{1}{Vm} \]

Sugestão

1. Experimente selecionar os extremos do gráfico de Michaelis-Mentem (curva hiperbólica), e observe os mesmos pontos no duplo-recíproco. Quais valores são mais confiáveis nesse último, os primeiros ou os últimos ?

2. Pesquise sobre outras formas de linearização (ex: Eadie-Hofstee; "v/S" X "v"), e veja como a transformação e seleção de pontos se apresenta. Para isso, altere as constantes abaixo:
    const invS = S.map(s => 1/s);
    const invV = V.map(v => 1/v);

1.11 Diagnóstico de Inibição Enzimática (Michaelis-Mentem e Lineweaver-Burk)

Contexto

Como apresentado acima e presente nos textos da área, é possível linearizar a curva de Michaelis-Mentem para uma observação mais simples ao diagnóstico de modelos de inibição enzimática. O objeto abaixo se propõe a essa interpretação. Para tanto, mantenha a enzima controle sem adição de inibidor no código (I=0). Para buscar um modelo de inibição, insira um valor para I e altere a(s) constantes de equilíbrio de dissociação do inibidor, kic e/ou kiu.

Sugestão

1. Simule as condições para uma inibição competitiva, inserindo um valor para o teor de inibidor ("I") e alterando o valor de "Km";
2. Faça o mesmo para um modelo incompetitivo, embora alterando o valor de "Vm";
3. Experimemente o modelo não competitivo puro, alterando "Km" e "Vm" para um mesmo valor;
4. Teste a inibição competitiva mista, inserindo valores distintos para "Km" e para "Vm."

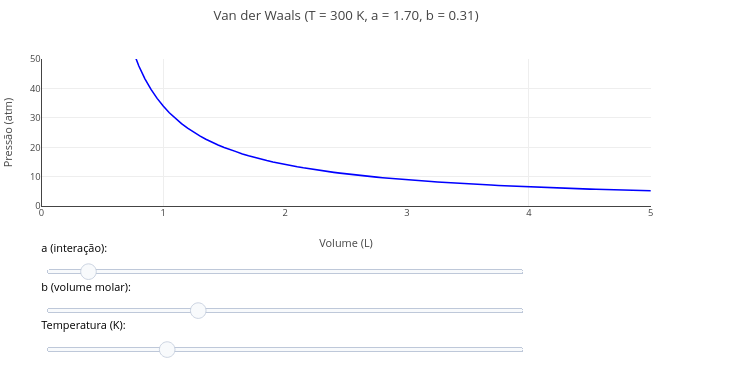
1.12 Equação de van der Waals para gases ideais

Contexto:

Uma adaptação que relaciona as quantidades termodinâmicas de pressão, volume e temperatura para gases ideais, é a equação de van der Waals. Nessa são computados coeficientes que estimam a existência de um volume e de interações inter-partículas. Dessa forma, a equação de van der Waals corrije a de gases ideais considerando um termo para compensação de forças intermoleculares (a/V$^{2}$) e o volume disponível, esse descontando o volume ocupado pelas próprias moléculas do gás.

Na simulação é oferecida uma interatividade adicional pela presença de sliders (controles deslizantes) para temperatura, e para os coeficientes de volume finito (b) e interação entre partículas (a).

Equação:

\[ P = \frac{RT}{V - b} - \frac{a}{V^2} \]

P = pressão do gás (atm);
V = volume molar (L);
T = temperatura (K);
R = 0,0821 = constante dos gases ideais (L·atm/mol·K);
a = constante de atração intermolecular (L$^{2}$·atm/mol$^{2})
b = constante de volume excluído (L/mol)

Sugestão:

1. Experimente variar os parâmetros da equação por meio do "slider" para temperatura, bem como para os coeficientes "a e b".
2. Discorra sobre qual dos coeficientes possui maior efeito no perfil da curva, e a razão para isso.

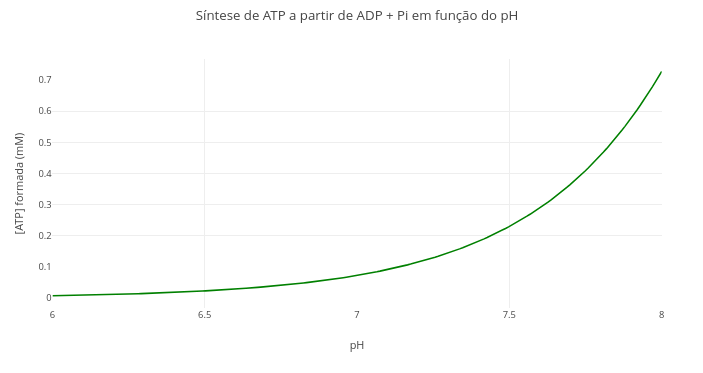
1.13 Equilíbrio de produção de ATP a partir de reagentes, temperatura, e pH

Contexto:

A produção de ATP intracelular envolve a relação clássica de equilíbrio químico entre reagentes e produtos em função da temperatura de reação, e ajustada para determinado valor de pH. Variando-se um e/ou outro teor de reagente, ou parâmetro físico-químico, é possível quantificar o produto pela reação termodinâmica que segue:

Equação:

\[ \Delta G = \Delta G^{\circ'} + RT \ln\left(\frac{[\text{ADP}] \cdot [\text{P}_i]}{[\text{ATP}]}\right) + 2{,}303 \cdot RT \cdot n_H \cdot \text{pH} \]

Onde,

$\Delta$G = energia de Gibbs da reação (positivo para síntese espontaneamente desfavorável, kJ/mol);
$\Delta$G$^{o'}$ = 30,5 kJ/mol energia de Gibbs padrão biológica para a síntese de ATP;
R = 8,314 J/mol/K (constante geral dos gases);
T=310 K (temperatura fisiológica);
nH$^{+}$ = 1 (número de prótons envolvidos na reação);
[ADP], [Pi], [ATP] = concentrações molares de reagentes e produto

Sugestão:

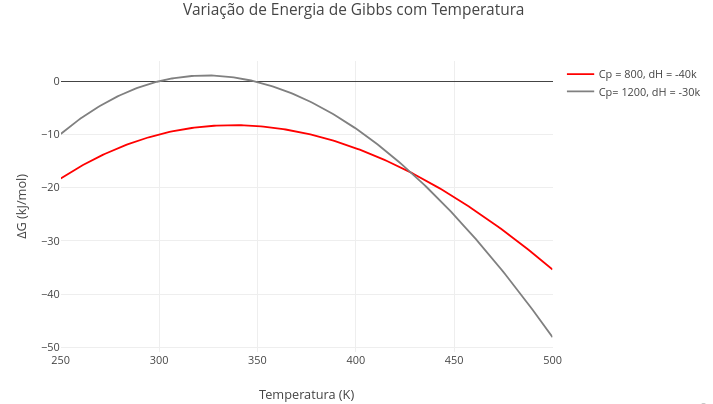
1. Altere as quantidades envolvidas na expressão, e compare com visualizações precedentes. Exemplificando, temperatura, pH, e teores de ADP e Pi.

1.14 Variação da energia de Gibbs com a temperatura

Contexto:

A relação de Gibbs-Helmholtz prevê que a energia de Gibbs varia de modo não linear com a temperatura, nas reações que envolvem mudança na capacidade calorífica do sistema ($\Delta$Cp). Essa forma expandida da equação de Gibbs para capacidade calorífica variável é apresentada em diversos fenômenos bioquímicos, tais como na transição de fases da estrutura de biomembranas submetidas à um desafio de compostos, ou na mudança conformacional que acompanha a estrutura proteica sob aquecimento. \

Equação:

\[ \Delta G(T) = \Delta H^\circ - T\,\Delta S^\circ + \Delta C_p \left(T - T_0 - T \ln\left(\frac{T}{T_0}\right)\right) \]

Onde,

$\Delta$G(T) = energia de Gibbs da reação em cada valor de temperatura, kJ/mol);
$\Delta$H$^{o}$ = entalpia padrão da reação a T$_{0}$, normalmente 298 K (J/mol);
$\Delta$S$^{o}$ = entropia padrão da reação a T$_{0}$;
$\Delta$Cp = variação da capacidade calorífica da reação (J/mol·K), assumida constante com a temperatura;
T = temperatura de interesse (K);
T$_{0}$ = temperatura de referência, geralmente 298 K.
R = 8,314 J/mol/K (constante geral dos gases);

Sugestão:

1. Experimente variar um ou mais parâmetros da expressão;
2. Teste o comportamento da curva de Gibbs em uma temperatura de referência elevada (simulação para organismo extremófilo);
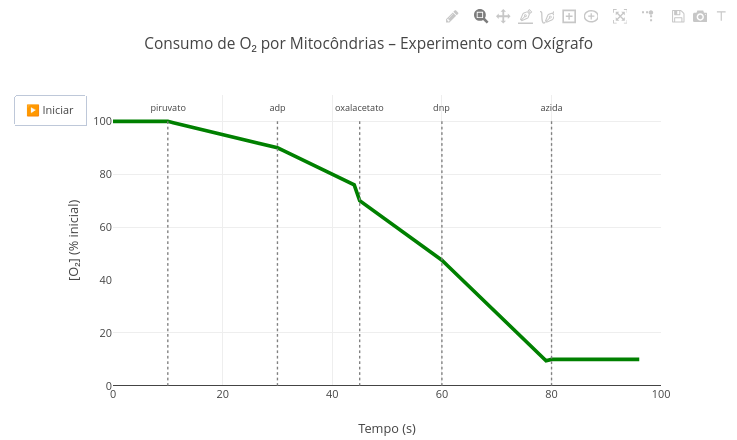
3. Simule a situação onde a variação da capacidade calorífica é nula

1.15 Consumo de Oxigênio por mitocôndria

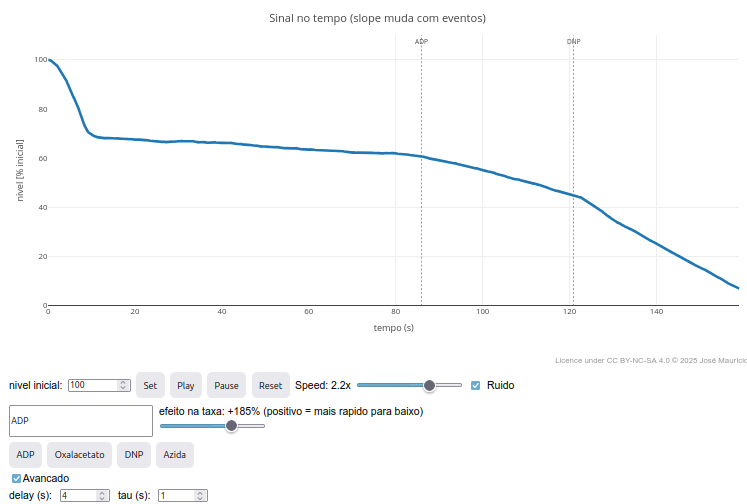
Contexto:

Oxígrafos são equipamentos que monitoram o teor de oxigênio dissolvido em solução. Diferente de oxímetros, baseados na medição de oxigenação de hemoglobina por clip direto na ponta de um dedo, oxígrafos são largamente utilizados em estudos de células vivas e suspensão de mitocôndrias.

O exemplo que segue ilustra uma animação para o teor de $O_{2}$ medido em oxígrafo para uma suspensão de mitocôndrias, e cujas taxas de consumo são variadas pelo uso de metabólitos modificadores (ex: piruvato, ADP, azida).

Sugestão:

1. Observe que o surgimento de metabólitos e as taxas de consumo de oxigênio decorrentes são definidas pela função "oxigenio". Experimente alterá-las e observe o efeito na animação;
2. Perceba que os metabólitos e sua atuação, bem como o sinal medido, teor de O2, são facilmente adaptados para qualquer outra medição metabólica no código. Experimente, por exemplo, como ficaria o gráfico numa simulação para a via glicolítica;
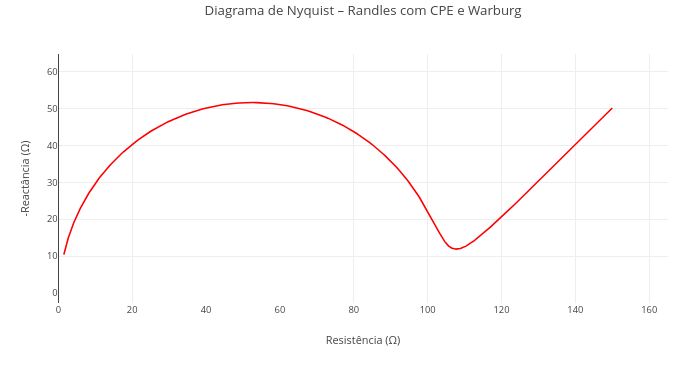
3. Esse código foi desenhado para uma animação. Vá até a seção de "Aplicativos" abaixo, e experimente o "FlowForces" para uma finalidade semelhante, embora com plena adaptação interativa.

1.16 Espectroscopia de impedância eletroquímica (EIS)

Contexto:

A espectroscopia de impedância eletroquímica (EIS) é uma técnica analítica que mede a resposta de um sistema eletroquímico a uma perturbação senoidal de pequena amplitude (ex: 5-10 mV), aplicada em uma ampla faixa de frequências (ex: 100 kHz-1mHz). A EIS permite obter-se informações sobre processos interfaciais, como transferência de carga, difusão de íons e formação de filmes passivos, por meio da análise da impedância complexa do sistema. Trata-se de uma técnica não destrutiva, amplamente utilizada em áreas como corrosão, baterias, células a combustível, biossensores e revestimentos protetores.

Equação:

Um modelo eletroquímico de impedância (EIS) com componentes típicos de circuitos equivalentes constitui o de Randles modificado: resistor série Rs, um resistor Rp em paralelo com um CPE (Elemento de Fase Constante), e um elemento Warburg. Uma representação comum para EIS é o gráfico de Nyquist, em que o eixo real representa resistência (Zre) e o eixo imaginário a reatância negativa (−Zim). O formalismo envolvido está na equação abaixo:

\[ Z_{\text{total}}(\omega) = R_s + \left[ \left( \frac{1}{R_p} + Q (j\omega)^n \right)^{-1} \right] + \frac{\sigma}{\sqrt{\omega}} (1 - j) \]

Onde:

Z$_{total}$ = impedância total em determinada frequência ;
$\omega$ = Frequência angular (rad/s), $\omega$=2πf ou $\omega$=2πf;
R$_{p}$ = Resistência ôhmica (resistência da solução eletrolítica, fios, contatos etc.) ;
R$_{p}$ = Resistência de polarização (associada a processos de transferência de carga, como reações eletroquímicas);
Q = Constante associada ao elemento de fase constante (CPE), substitui um capacitor ideal para representar comportamentos não ideais ;
n = Expoente do CPE, entre 0 e 1; define o grau de idealidade do comportamento capacitivo (n = 1: capacitor ideal; n < 1: dispersão);
$\sigma$ = Coeficiente de Warburg, associado à difusão de íons no sistema eletroquímico ;
j = Unidade imaginária, j$^{2}$ = −1;

Sugestão

1. Verifique o efeito de Rs no gráfico, anulando o seu valor (resistência da solução);
2. Observe a deformação do semicírculo variando os valores do elemento de fase constante (ex: Q = 1e-3; n = 0.6 - dispersão do comportamento capacitivo);
2.  Experimente combinar outros valores dos parâmetros do cabeçalho do código, para evidenciar situações correntes em eletroanálise: Rs, Rp, Q, n, e sigma;
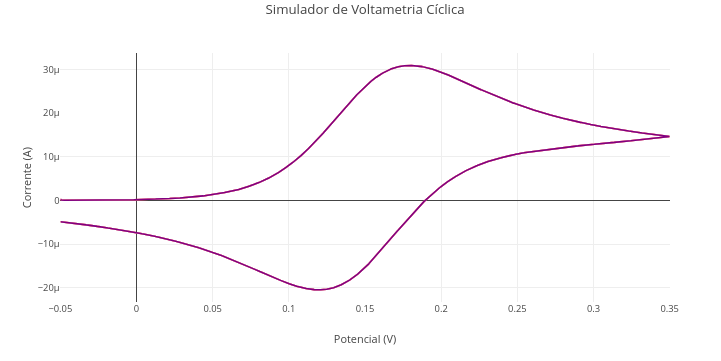
3. Reduza o modelo de Warburg com elemento de fase constante a um modelo de Randles simples, e formado apenas por 2 resistores em série, o segundo em paralelo com um capacitor ideal, e sem difusão de Warburg (sigma = 0; n = 1).

1.17 Voltametria cíclica

Contexto:

A voltametria cíclica (VC) é uma técnica eletroanalítica para caracterização de processos redox interfaciais (eletrodo-solução). Quando utilizado um analito padrão em equilíbrio quantitativo entre as formas oxidada e reduzida, o gráfico resultante adquire um perfil incomum, e denominado duck shape, ou forma de pato. Isso decorre do formato peculiar frente a uma varredura potenciométrica bidirecional sobre um conjunto de eletrodos por um potenciostato, e resultando em ciclos de oxidação e posterior redução (aplicação de potenciais positivos seguido de negativos). A forma, o valor e a distância entre os picos resultantes permitem identificar e caracterizar o analito, bem como seus processos redox envolvidos no experimento.

Equação:

Embora o formalismo para voltametria cíclica seja complexo e envolva a solução de equações diferenciais ordinárias (bem como as técnicas eletroanalíticas, de modo geral), estando distante do objetivo deste material, pode-se resumir o fluxo de corrente resultante pela equação de Buttler-Volmer que segue:

\[ j = j_0 \left[ \exp\left(\frac{\alpha n F (E - E^0)}{RT}\right) - \exp\left(\frac{-(1 - \alpha) n F (E - E^0)}{RT}\right) \right] \]

Onde:

j = densidade de corrente;
j$_{0}$ = corrente de troca;
$\alpha$ = coeficiente de transferência de carga;
E = potencial aplicado ao eletrodo;
E$^{0}$ = potencial padrão do eletrodo;
n = número de elétrons;
F = constante de Faraday (96485 C·mol⁻¹)
R = constante geral dos gases (8.314 J·mol⁻¹·K⁻¹);
T = temperatura

Para um modelo de difusão de eletroanalito e acúmulo na superfície eletródica, a equação geral para a condição de contorno onde a taxa de conversão redox é proporcional à corrente de difusão, pode ser representada pela equação da 2a. Lei de Fick para transporte de massa:

\[ \frac{\partial C(x,t)}{\partial t} = D \frac{\partial^2 C(x,t)}{\partial x^2} \]

Onde:

C(x,t) = concentração da espécie eletroanalítica (mol/cm³), em função da posição x e do tempo t;
D = coeficiente de difusão da espécie (cm²/s);
t = tempo (s);
x = distância da superfície do eletrodo (cm);
$\delta$ = notação para derivada parcial.

O equilíbrio químico da reação redox é dado pela razão entre as concentrações da forma oxidada e reduzida na interface eletrodo/solução quando o sistema está em equilíbrio (ou quase-equilíbrio), conforme a equação de Nernst:

\[ E = E^0 + \frac{RT}{nF} \ln \left( \frac{[\text{Ox}]}{[\text{Red}]} \right) \]

A corrente resultante é obtida pela Lei de Faraday:

\[ i(t) = n F A D \left. \frac{\partial C(x,t)}{\partial x} \right|_{x=0} \]

Onde:

A = área de superfície eletródica (cm²);
i(t) = corrente no tempo t (A, Àmpere).

Simulador de Voltametria Cíclica

Para ilustrar o potencial da plataforma JSPlotly/GSPlotly para o desenvolvimento de experimentos virtuais complexos, segue um simulador de voltametria cíclica resultante dos procedimentos acima (bem como de algumas horas de engenharia de prompt!!).

O exemplo ilustra um comportamento típico em voltametria cíclica (e o curioso duck shape), e contempla uma modelagem de difusão e acúmulo de espécies eletroativas próximo à superfície do eletrodo. O código utiliza uma solução numérica para obter a densidade de corrente ao longo do tempo, considerando os efeitos da varredura cíclica do potencial aplicado, o transporte de massa, e a cinética da reação.

Em suma, resolve numericamente a equação de Fick com condição de contorno dinâmica, aplica a equação de Nernst na fronteira (superfície do eletrodo) para determinar a conversão entre espécies, usa o método das diferenças finitas ou esquema explícito para avançar no tempo, e obtém a corrente aplicando a Lei de Faraday, pela derivada do fluxo na interface.

Achou complexo ? Então que tal: o código une Fick (transporte) e Nernst (equilíbrio redox local) para modelar com precisão a forma do voltamograma, obtendo-se uma simulação física com realismo significativo para voltametria cíclica.

Sugestão:

1. Observe o quantidade de valores ao início do código, tangíveis a uma "manipulação paramétrica". Procure saber o que representam, e busque variar seus valores de modo consciente, objetivando agregar valor ao aprendizado da simulação. Essa é a alma da "manipulação paramétrica" que envolve o "ensino reprodutível" !!

1.18 Diagramas e fluxogramas

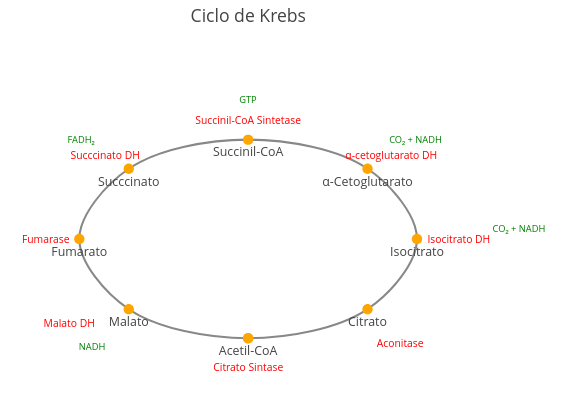
Contexto: Diagrama

Pela natureza da biblioteca Plotly.js, também é possível a geração de códigos no JSPlotly sem o envolvimento de uma equação, tal como para representação de diagramas e fluxogramas, entre outros. O exemplo abaixo ilustra uma representação do ciclo de Krebs, e o seguinte um fluxograma experimental.

Sugestão:

1. Experimente reposicionar melhor enzimas e metabólitos, apenas clicando e arrastando os termos;
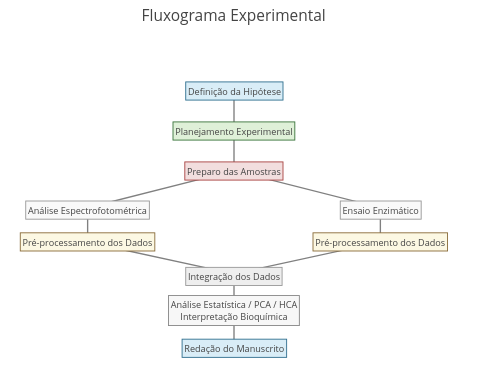
2. Experimente substituir os nomes que estão no código para a produção de outro ciclo metabólico, como o ciclo da ureia.

Contexto: Fluxograma

Sugestão:

1. Reposicione termos e conectores com arraste de mouse;
2. Para um fluxograma diferente no conteúdo, modifique os termos no código;
2. Para um fluxograma diferente no formato, altere as características de fonte e conectores na constante "annotations".

2 Construção de gráficos

Embora grande parte de gráficos representativos envolva apenas linhas e/ou pontos num plano, a biblioteca Plotly.js é pródiga na elaboração de um conjunto significativo de tipos variados, tal como representado na sua versão para a linguagem R no site do desenvolvedor.

Além disso, mesmo para um gráfico simples de pontos e/ou linhas, é possível um grande número de configurações distintas e widgets interativos, alguns dos quais são representados a seguir.

2.1 Gráfico com 2 eixos de ordenadas

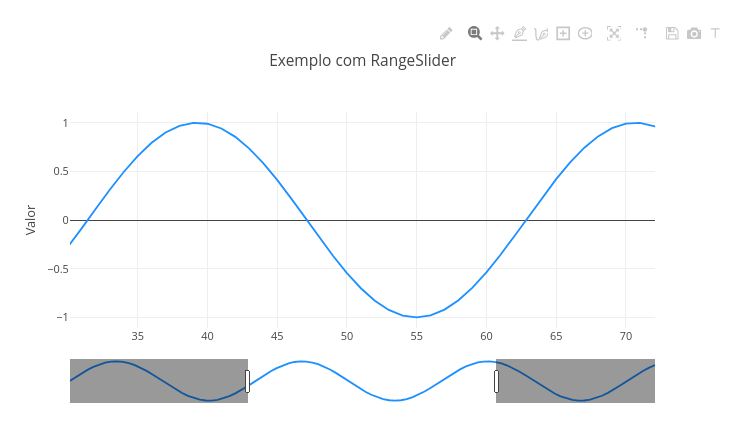
2.2 RangeSlider

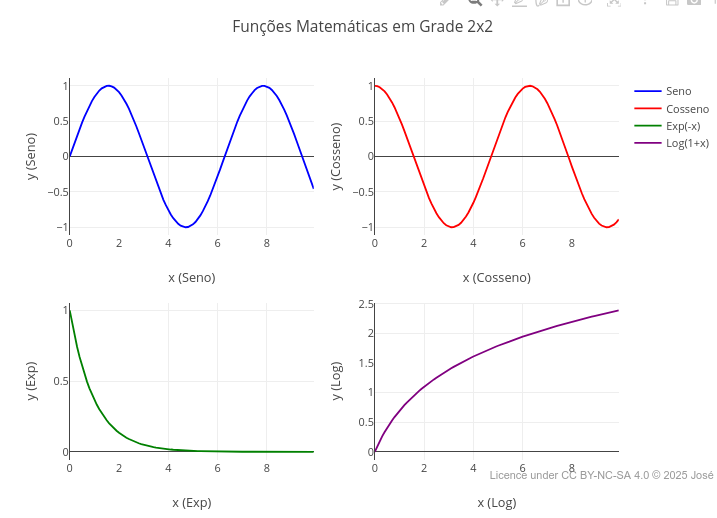
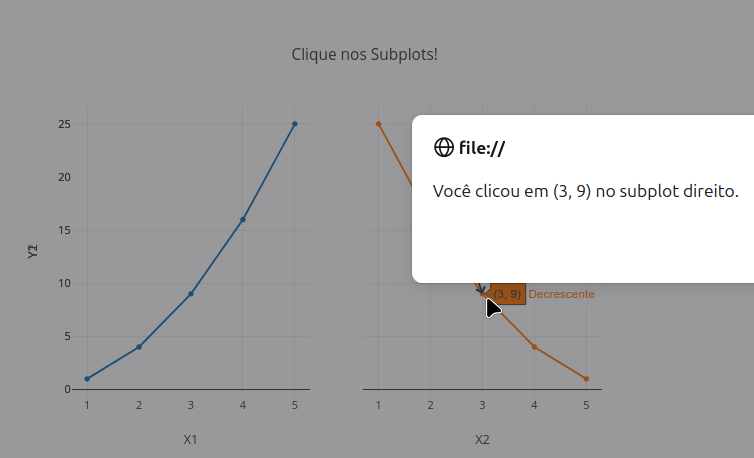
2.3 Subplots

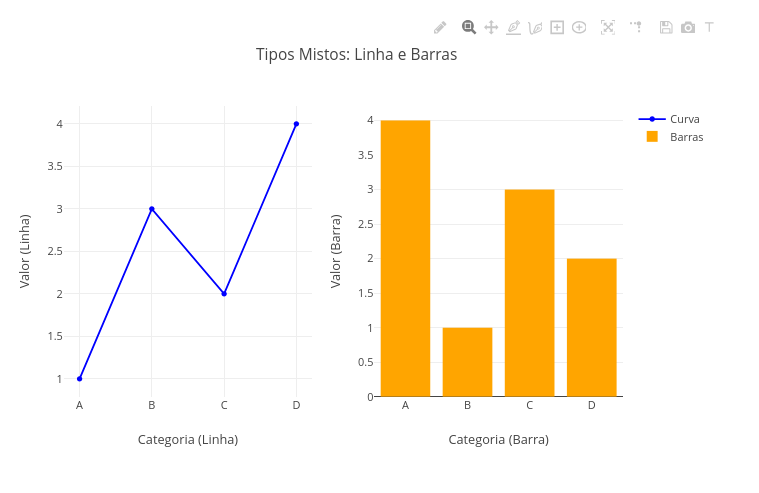
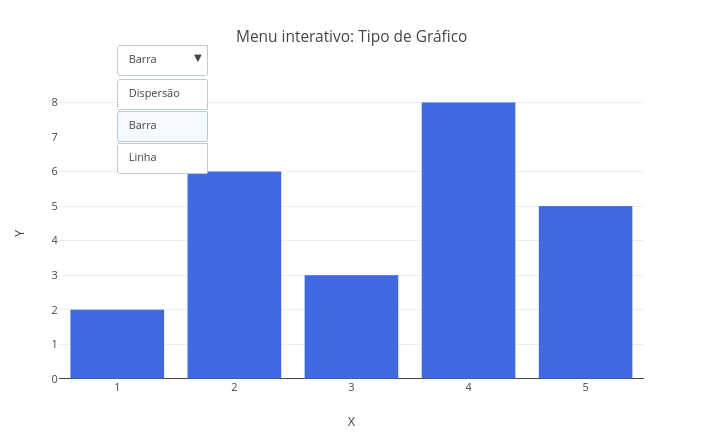
2.4 Subplots com tipos diferentes

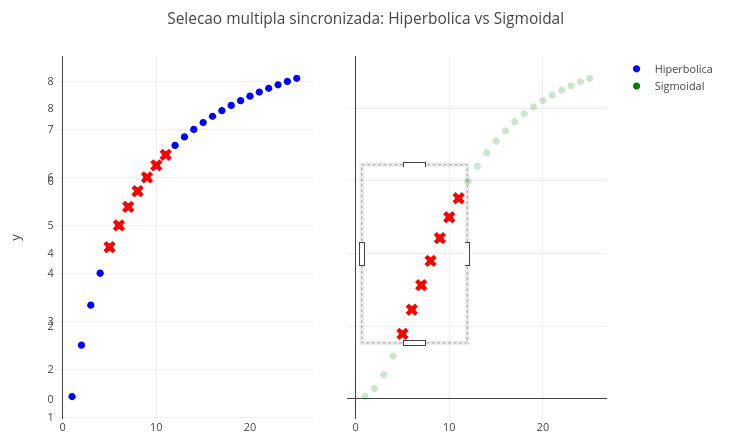
2.5 Seleção múltipla sincronizada

2.6 Evento de clique & mensagem

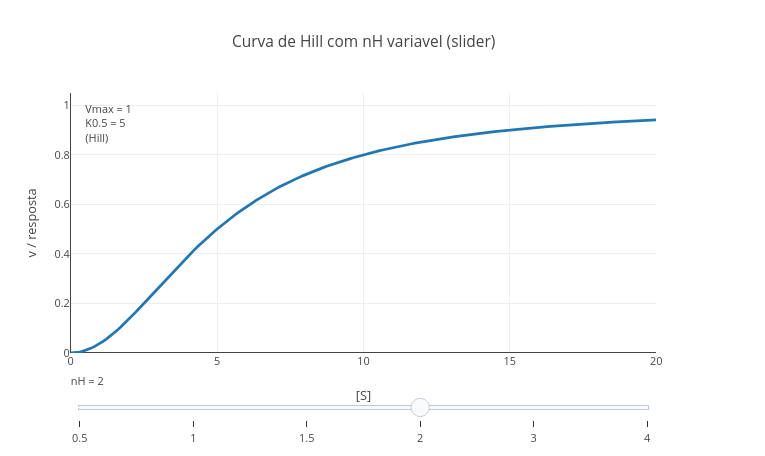
2.8 Controle deslizante (slider)

3 Análise de dados

3.1 Inserção de dados do usuário

Contexto

Por vezes é interessante trabalhar-se com os próprios dados discretos, buscando-se uma relação de tendência, matemática ou simplesmente visual, para a relação de variáveis. Segue um exemplo de gráfico interativo com dados do usuário.

Sugestão:

1. Experimente alterar os dados inseridos, sobrepondo ou não o gráfico;
2. Experimente alterar a representação de dados em "mode" e "type", para pontos, linhas, pontos+linhas, barras.

3.2 Carregamento de arquivo para análise

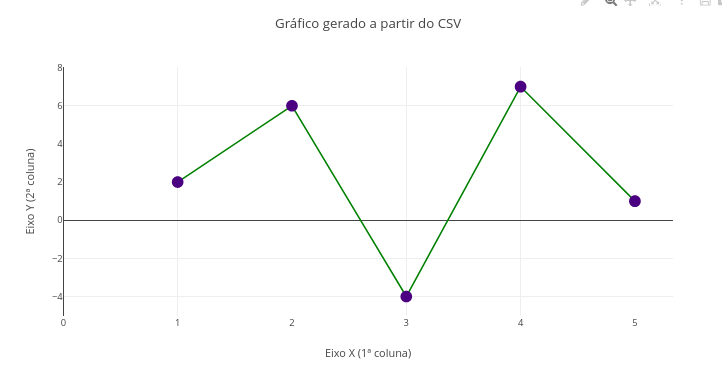
Contexto - Arquivo CSV

Por vezes, há necessidade de se analisar resultados referentes a um conjunto de dados presente numa planilha. Para essa situação, o exemplo a seguir ilustra o carregamento de dois vetores de dados a partir de um arquivo CSV (comma separated value), formato comumente utilizado em exportação/importação em planilhas eletrônicas, e seu gráfico resultante.

Instruções:

1 Clique em add plot e selecione um arquivo CSV no botão browse superior que é apresentado. Nota: variável X na 1a. coluna do arquivo, e variável Y na 2a. coluna;
1. Clique em add plot novamente para a visualização do gráfico resultante.

Sugestão

1. Experimente outros arquivos CSV;
2. Varie os aspectos do gráfico, como tipo, cor, tamanho do marcador, etc.

3.3 Ajuste linear de dados

Contexto:

Em diversas situações da pesquisa experimental, faz-se necessário correlacionar os dados de uma variável dependente com uma variável preditora frente à equação que segue.

Equação:

\[ y = \alpha x + \beta + \varepsilon \]

Onde:

y = variável dependente;
x = variável independente;
$\alpha$ = inclinação da reta ajustada (slope);
$\beta$ = intercepto da reta ajustada;
$\epsilon$ = erro da medida.

Pode-se obter os parâmetros de inclinação e intercepto por alguns procedimentos, como mínimos quadrados, álgebra matricial, ou por somatórias simples. Nesse último caso, o cálculo de parâmetros e de erro pode ser computado como segue:

\[ \alpha = \frac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - \left( \sum x_i \right)^2} \]

\[ \beta = \frac{\sum y_i - \alpha \sum x_i}{n} \]

\[ \hat{y}_i = \alpha x_i + \beta \]

\[ \varepsilon_i = \left| y_i - \hat{y}_i \right| \]

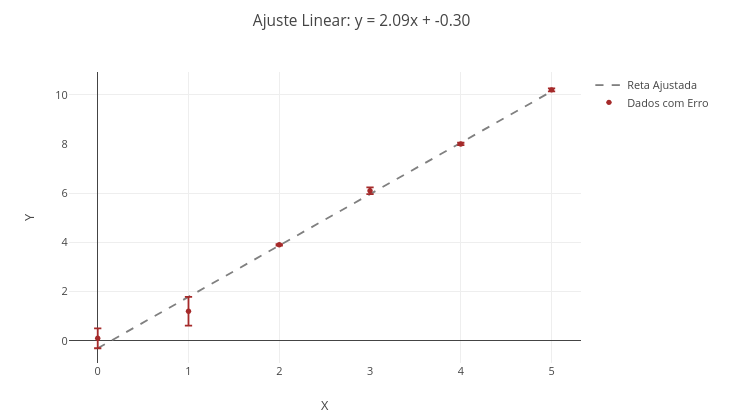
Uma representação para ajuste linear com dados arbitrários é fornecida abaixo:

Sugestão:

1. Apresente os pontos sobrepostos ou não à reta do ajuste. Para a sobreposição, escolha "mostrarPontos = true" e "mostrarReta = true";
2. Altere os dados e realize novo ajuste, para obtenção de outros parâmetros da reta.

3.4 Regressão polinomial

Contexto:

Em algumas situações, o ajuste linear não confere uma tendência adequada para modelagem de dados experimentais, o que suscita o emprego de outros modelos, tais como exponencial, hiperbólico, logarítmico, de potência, e polinomial. Tendências polinomiais são comuns em fenômenos naturais, com o tratamento matemático dos dados ocorrendo por diferentes métodos, como somatórias simples, mínimos quadrados, ou álgebra linear. Segue um exemplo de regressão polinomial com graus ajustáveis no código.

3.4.1 Equação

A minimização de erros para a curva polinomial é obtida por uma regressão por mínimos quadrados generalizada, e aplicação de matriz de Vandermonde, como segue.

Seja os vetores x=[x$_{1}$,x$_{2}$,…,x$_{n}$] e y=[y$_{1}$,y$_{2}$,…,y${_n}$], deseja-se ajustar o polinômio:

\[ y = \beta_0 + \beta_1 x + \beta_2 x^2 + \cdots + \beta_g x^g \]

Dessa forma, elabora-se a matriz de Vandermonde como:

\[ X = \begin{bmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^g \\\\ 1 & x_2 & x_2^2 & \cdots & x_2^g \\\\ \vdots & \vdots & \vdots & & \vdots \\\\ 1 & x_n & x_n^2 & \cdots & x_n^g \end{bmatrix} \]

Para encontrar os coeficientes $\beta$ que minimizem o erro quadrático, soluciona-se o sistema linear em sequência:

\[ \boldsymbol{\beta} = (X^T X)^{-1} X^T \mathbf{y} \]

Onde:

T representa a matriz transposta

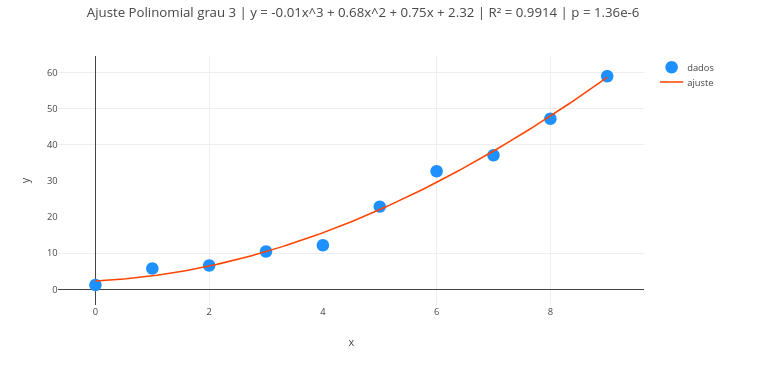
Sugestão:

1. Experimente o grau 1 para o polinômio, ou seja, uma redução do tratamento ao ajuste linear;
2. Altere a formatação de rótulos, cores, tamanhos, etc, no código;
3. Sobreponha alguns ajustes, edite e reposicione a legenda;
4. Teste o código com outro vetor de dados.

3.5 Regressão multilinear

Contexto:

Ajuste linear múltiplo é de grande utilidade quando se deseja prever um comportamento em função de duas ou mais variáveis preditoras. O procedimento envolve uma matriz de projeto (ou operador de projeção) similar à matriz de Vandermonde.

Equação:

A solução analítica para a matriz de projetos envolve resolver uma matriz de coeficientes $\beta$ para um conjunto de valores preditores do vetor de resposta y, como segue:

\[ y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \cdots + \beta_p x_{pi} + \varepsilon_i \]

\[ \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon} \]

\[ \hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y} \]

Onde:

$\beta$ = vetor de coeficientes;
y = vetor de respostas;
X = matriz de projeto;
$\epsilon$ = ruído aleatório

Dessa forma, valores preditos e erro associado são obtidos por:

\[ \hat{\mathbf{y}} = \mathbf{X} \hat{\boldsymbol{\beta}} \]

\[ \mathbf{e} = \mathbf{y} - \hat{\mathbf{y}} \]

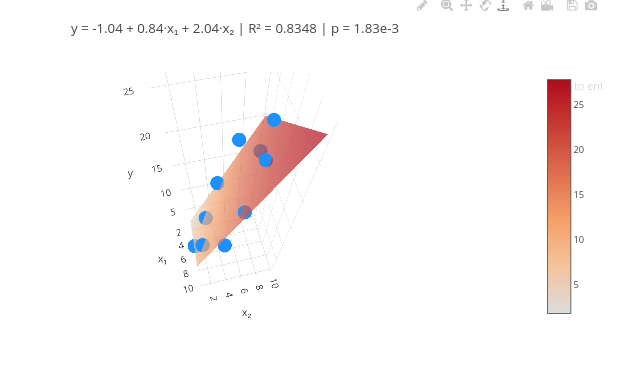
Por óbvio, a representação gráfica para um ajuste multilinear está limitada a duas variáveis independentes, x1 e x2, além da variável resposta (gráfico 3D), embora o cálculo matricial permita diversas variáveis preditoras (espaço hiperdimensional). Tangente à primeira situação, segue um exemplo.

Instruções

Observer que há um flag booleano (mostrarAjuste) ao início do código: false para dados somente, e true para o ajuste;
Pode-se clicar em add plot para visualizar os dados com o flag em false, seguido de outro add plot com o flag em true.

Rotacione o gráfico e observe a superfície em torno dos pontos. Diferente de um ajuste linear, os pontos estão distribuídos de forma não contínua no espaço.

Sugestão:

1. Resultados de QSAR ("Quantitative Structure-Activity Relationship") utilizam análise por ajuste multilinear para identificar a força das variáveis preditoras. Experimente na internet um conjunto de dados que possua 2 variáveis (ex: concentração, pH, composto A, B, etc.)
2. Para mais variáveis preditoras, veja o código que segue !!

3.6 Ajuste linear múltiplo com 3 ou mais variáveis preditoras

Contexto

Embora o JSPlotly tenha sido concebido para a produção de gráficos e mapas interativos com uso da biblioteca Plotly.js sobre os ombros da linguagem JavaScript, essa extende as possibilidades de aplicação além das representações gráficas. Um exemplo disso permeia o código que segue, para um ajuste multilinear para uma situação com 4 variáveis preditoras.

Sugestão:

1. Experimente variar o número de preditores (xi). Para isso:
  a. Sem quiser reduzir, basta retirar o(s) vetor(res) desejados, e corrigir seu quantitativo na linha: "const X = x1.map((_, i)";
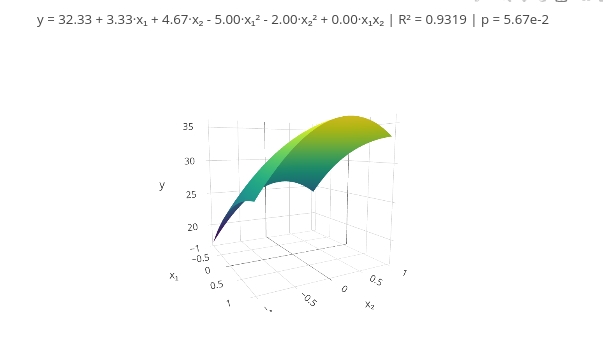
  b. Se quiser aumentar, acrescente um novo vetor na linha correspondente, e atualize o quantitativo no mapeamento de "const X = x1.map((_, i)".

3.7 Metodologia de Superfície de Resposta (MSR)

Contexto

Uma variação de ajuste multilinear envolve a metodologia de superfície de resposta, comumente linear (plano) ou quadrática (curvilinear), aplicada em modelagem e otimização de processos experimentais com múltiplas variáveis independentes. Seu objetivo é ajustar uma equação matemática que represente a relação entre os fatores experimentais e a variável resposta, permitindo prever comportamentos e identificar condições ótimas.

Para experimentos com dois fatores, utiliza-se comumente um modelo quadrático de segunda ordem, o qual permite representar superfícies com curvatura. A ideia central do experimento é selecionar valores e seus códigos (-1,0,1), representando, respectivamente, uma quantidade abaixo, uma quantidade média, e uma acima, para determinada variável preditora.

Equação:

O modelo geral quadrático para 2 fatores é representado por:

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{11} x_1^2 + \beta_{22} x_2^2 + \beta_{12} x_1 x_2 + \varepsilon \]

Com a forma matricial do modelo representada por:

\[ \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon} \]

E a estimativa dos coeficientes $\beta$ por mínimos quadrados, de modo similar ao ajuste multilinear, por:

\[ \hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y} \]

Sugestão:

1. Como sugerido anteriormente, experimente utilizar dados da literatura ou de outra fonte cujas respostas já são conhecidas, substituindo os respectivos vetores ao início do código. Isso permite comparar a eficácia de uso da ferramenta apresentada.

3.8 Suavização de dados - Spline e filtro de Savitzky-Golay

Em pesquisa experimental a detecção de sinais ocasionalmente ocorre na presença de níveis significativos de ruído, tal como ocorre em varredura contínua espectral sob variação de comprimento de onda, ou na detecção de sinais elétricos no tempo. Nesse caso, não há uma equação analítica que descreva o comportamento do sinal, embora algumas ferramentas de processamento digital possam confiar uma curva de tendência no tratamento de dados, reduzindo significativamente o nível de ruído, tais como por curva de spline e filtro de Savitzky-Golay.

Contexto - Spline cúbica

Uma técnica de interpolação bastante comum refere-se ao uso de spline cúbica por polinômios de grau 3 interconectando janelas de dados. O tratamento consiste em aplicar as funções polinomiais em subintervalos dos pontos, promovendo uma suavização entre as janelas de dados.

Equação

Matematicamente, a spline é aplicada de tal forma que:

\[ S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3 \]

Onde:

S$_{i}$(x) = função spline cúbica no intervalo [xi,xi+1];
a$_{i, b${i}$, c${i}$, d$_{i}$ = coeficientes específicos para o segmento i;
x$_{i}$ = ponto inicial do intervalo;
x = variável independente.

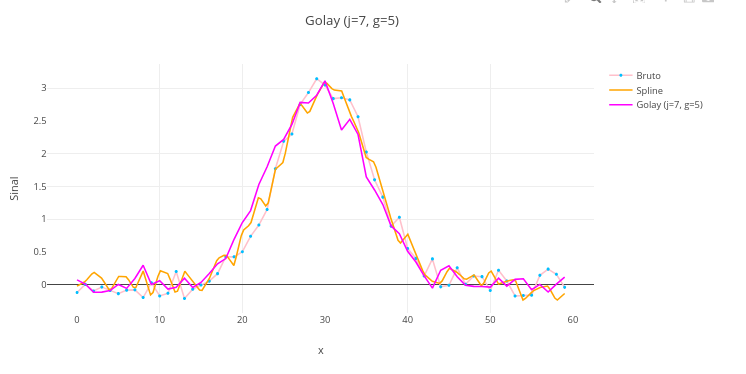
Contexto - Filtro de Savitzky-Golay

Já a técnica de suavização por filtro de Savitzky-Golay aplica uma regressão polinomial local a uma janela móvel, por mínimos quadrados e grau pré-determinado, preservando sinais de picos, vales e bandas. Distinto da spline cúbica, o filtro produz uma curva contínua global, e não um conjunto de curvas interconectadas.

Equação

Matematicamente:

\[ \tilde{y}_i = \sum_{j=-m}^{m} c_j \cdot y_{i+j} \]

Onde:

y$_{i}$ = valor suavizado na posição i;
y$_{i+j}$ = valores reais da série dentro da janela;
c$_{i}$ = coeficientes do filtro derivados de uma regressão polinomial;
m = número de pontos de cada lado da janela central.

Segue um exemplo de código para o JSplotly e que ilustra o uso dos dois métodos de interpolação.

Instruções:

1. O código possui dois flags true/false, um para “usarGolay” e outro para “usarSpline”;
1. Visualize os dados brutos adotando false para ambos os flags;
1. Para sobrepor uma spline cúbica mude sua constante para true;
1. Para sobrepor o filtro de Savitzky-Golay, mude sua constante para true;
1. Para ajustar o filtro, modifique seus parâmetros nas constantes janela (janela móvel) e/ou grau (grau do polinômio).

Sugestão:

1. Compare os efeitos de suavização pelos dois tratamentos de interpolação polinomial;
2. Aplique apenas o filtro, ajustando parâmetros de janela móvel e grau polinomial;
3.  Experimente a interpolação com outros dados brutos no código, substituindo as constantes "x_values" e "y_raw" por vetores numéricos;

3.9 ANAVA e teste de Tukey-HSD

Contexto:

Em pesquisa é comum proceder a análise de um conjunto de dados comparando-se a variância entre grupos com a obtida dentro de cada grupo, ou Análise de Variância (ANAVA). Uma vez obtida a informação estatística de que há diferença entre os grupos superior à interna, procede-se um teste pos-hoc para comparação de médias, como o teste de Tukey-HSD (Honest Significant Difference).

Equação:

A equação que caracteriza um teste de Tukeu-HSD é fornecida abaixo (correção para grupos desbalanceados):

\[ \text{HSD}_{ij} = q_{\alpha} \cdot \sqrt{\frac{\text{MS}_{\text{within}}}{2} \left( \frac{1}{n_i} + \frac{1}{n_j} \right)} \]

Onde:

HSD = valor mínimo da diferença entre duas médias para que ela seja considerada significativa;
q$_{\alpha}$ = valor crítico da distribuição studentizada q (distribuição de Tukey), dependendo do número de grupos e do nível de significância $\alpha$;
MS$_{within}$ = quadrado médio dentro dos grupos (erro) obtido da ANAVA;
n: número de observações por grupo (i e j se houver grupos de tamanhos diferentes).

Sugestão:

1. Você pode clicar e arrastar os marcadores de mínima diferença (a,b,etc) acima do gráfico, para melhor ajuste visual, bem como a tabela de ANAVA e o resultado do teste estatístico;
2. Altere os valores dos vetores, refaça a análise e o gráfico simultâneos, e perceba a diferença nos valores obtidos. Observe que, como informado na borda inferior, é necessário atualizar a página do site para anular dados anteriores retidos em memória cache;
3. Insira outros dados nos vetores respectivos, seus ou de outra fonte;
4. Insira novos vetores de dados, ou delete algum, para um cálculo e gráfico personalizado.

3.10 Ajuste não linear de dados

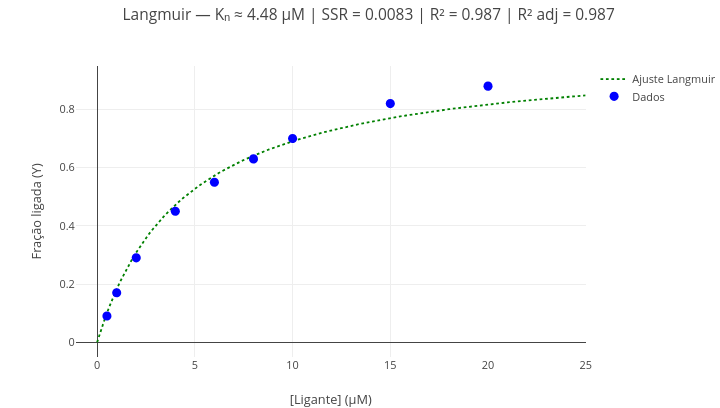
Modelagem é uma área de emprego comum nas ciências naturais, quando se deseja previsão ou correlação matemática de dados experimentais. Modelos podem constituir-se lineares ou não. Quando não lineares, podem ser aplicados de forma empírica para os dados (ex: funções quadráticas, logarítmicas, exponenciais ou de potência), ou a partir de uma função matemática explanatória do modelo.

Nesse caso são empregadas técnicas para ajuste não linear dos dados ao modelo, como Simplex, Gauss, Newton-Raphson, Levenberg-Marquadt, ou mínimos quadrados por exemplo. Seja qual for o método, o ajuste não linear difere-se do linear em pressupostos e tratamento dos dados (veja uma rápida explicação aqui.

Contexto: Interação ligante-proteína (algoritmo de grid search)

O exemplo a seguir ilustra a aplicação de um ajuste não linear de dados de interação molecular por modelo de Langmuir, e tratamento por minimização do erro quadrático por varredura manual. Nesse tratamento, calcula-se a soma dos erros quadráticos (RMSE) para combinações de a e b, selecionando-se o par com menor erro calculado. Nesse caso, por simplificação, apesar do JSPlotly trabalhar com bibliotecas mais específicas, a regressão não linear dá-se por mínimos quadrados, mas realizada por grid search, e não por métodos iterativos clássicos. Assim, um conjunto de valores é testado para o par (a, b) em uma malha definida previamente (tabela de combinações), permitindo a identificação dos parâmetros que melhor descrevem os dados experimentais segundo o critério de erro mínimo.

Equação:

A equação de Langmuir é representada abaixo:

\[ Y = \frac{aX}{K_d + X} \]

Onde:

Y = fração de sítios ocupados;
X = concentração do ligante livre;
a = valor de saturação (sítios de mesma afinidade completamente ocupados);
Kd = constante de equilíbrio de dissociação do complexo.

Nesse caso, a função de mínimos quadrados não linear fica:

\[ SSR(a, K_d) = \sum_{i=1}^n \left( y_i - \frac{a x_i}{K_d + x_i} \right)^2 \]

Onde:

SSR = soma dos quadrados dos resíduos (inversamente propocional à qualidade do ajuste)

Sugestão:

1. Como no exemplo anterior, apresente alternativamente os pontos e a curva de ajuste pela operação "booleana" ("mostrarPontos = true/false"; "mostrarCurva = true/false");
2. Altere os dados e realize novo ajuste, para obtenção de outros parâmetros da equação (Kd, SSR, R², R² ajustado). Obs: R² adj corresponde ao valor de R² corrigido para o número de parâmetros do modelo (no caso, "2"), incidindo diretamente nos "graus de liberdade" para o ajuste.

Contexto - Inibição competitiva em cinética enzimática (algoritmo de Gauss-Newton)

O método de Gauss-Newton ajusta iterativamente modelos não lineares a conjuntos de dados experimentais. Ele é especialmente eficiente quando o modelo é quase linear em relação aos parâmetros e os resíduos são moderadamente pequenos. O objetivo é encontrar os parâmetros $\theta$ que minimizam a soma dos quadrados dos resíduos entre os dados observados yi e os valores preditos pelo modelo f(xi,$\theta$. Diferente do método de Newton-Raphson completo, o Gauss-Newton evita o cálculo explícito da Hessiana, utilizando uma aproximação baseada na Jacobiana dos resíduos.

Equação:

Essa aproximação resulta em um sistema linear que pode ser resolvido a cada iteração para atualizar os parâmetros do modelo. A fórmula central do método consiste na multiplicação da Jacobiana transposta JT pela própria Jacobiana J, formando uma matriz simétrica que aproxima a Hessiana. O vetor de resíduos r é então usado para determinar a direção de atualização $\Delta\theta$, com a seguinte equação:

\[ \theta_{k+1} = \theta_k + \left(J^T J\right)^{-1} J^T \cdot r \]

Para ilustrar o potencial do aplicativo em ajuste não linear iterativo, segue um exemplo para cinética enzimática utilizando-se um modelo de inibição competitiva.

O código permite ajustar as sementes, tolerância, e número de iterações, e oferece o gráfico (pontos/linha ajustada, manualmente), e parâmetros estatísticos da regressão.

Instruções

1. Perceba que o código possui um flag para true/false na constante ajuste. Deixe-o em false para a representação dos dados, somente (vetores x e y, ou S e v);
1. Na área da Plot do código, acerte a constante trace para que fique com os vetores de dados, também;
1. Clique em add plot para visualizar os pontos experimentais;
1. Para superimpor a curva ajustada, atualize as constantes ajuste e trace (vetores S_fit e v_fit), e escolha lines em mode.

4 Aplicativos

4.1 prot.Id - Experimentação simulada para caracterização de aminoácidos e cadeias

Contexto:

O JSPlotly permite se trabalhar com um conjunto de interações não necessariamente atreladas à equações e suas representações gráficas. O exemplo a seguir ilustra seu potencial para uma simulação de um experimento clássico em Bioquímica: a caracterização de aminoácidos, peptídios, e proteínas, por reações cromogênicas em tubos de ensaio. Como o escopo deste material é apresentar e facultar o uso de OIERs variados (objetos interativos de ensino reprodutível), recomenda-se ao usuário a busca de fontes de informação tangentes às reações descritas brevemente a seguir.

Instruções do simulador

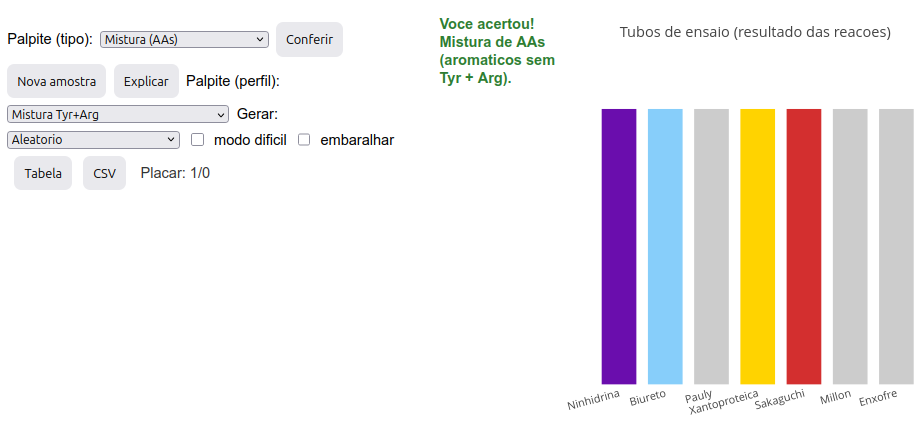
O simulador permite duas opções: a) descobrir a natureza de uma amostra ou b) descobrir o padrão de cores de reações para uma amostra escolhida.

Opção A: descobrir a natureza de uma amostra:

Aqui é possível “jogar” para verificar se está diante de uma amostra de proteína/peptídio (cadeia), de um aminoácido (AA), de uma mistura específica de AAs, ou de de AA(s) presente numa cadeia. Para isso:

Clique na imagem abaixo e dê um “add”. Será gerado um conjunto de 7 barras coloridas, representando as cores obtidas em tubos de ensaio para 7 reações distintas para caracterização proteica: ninhidrina, biureto, Pauly, xantoproteica, Sakagushi, Millon, e enxofre (Cys);
Descubra o tipo de amostra em função do padrão de cores dos tubos apresentado, fornecendo um palpite. O palpite deve ser por tipo (no menu “Palpite (tipo)” - AA, cadeia, ou mistura de AAs) e por perfil (no menu “Palpite (perfil)” - aleatório, AA(s) específico(s) ou mistura específica);
Após a seleção nos 2 menus, clique em “Conferir”. Se tiver acertado, um “Placar” logo abaixo irá computar o número de acertos/número de amostras “jogadas”;
Se errar, tente de novo ou busque a explicação do padrão de cores em “Explicar”;

Existem duas outras possibilidades: “Modo difícil”, que esconde o nome das reações, embora mantendo sua sequência, e “Embaralhar”, que altera a ordem dos tubos;
Para uma nova amostra, basta clicar em “Nova amostra”;

Opção B: descobrir o padrão de cores de uma reação para uma amostra selecionada:

Selecione uma amostra em “Gerar”, e clique em “Nova amostra”. Será gerado um conjunto de tubos com o padrão de reações esperado para a amostra.

Sugestão:

1. Experimente clicar em "Nova amostra" para verificar a frequência de possibilidades;
2. Experimente as duas opções de operação do "jogo" (sim, é um jogo...afinal, tem um placar!);
3. Experimente o "modo difícil" (sem referência às reações em sequência) ou "embaralhar" (permuta da ordem das reações). Por óbvio, contudo, evite os dois simultaneamente !

4.2 ZeMol - Visualizador 3D para modelos moleculares

Contexto:

Pelas características combinadas do uso de JavaScript e da biblioteca Plotly.js, é possível extender o potencial de aplicação do JSPlotly para a construção de verdadeiros aplicativos HTML. Um claro exemplo desse alcance é ilustrado abaixo, para um visualizador molecular de natureza similar a alguns pré-existentes e empregados em ensino e pesquisa (Jmol, Pymol, etc).

Embora seja obviamente bem menor na extensão de suas funcionalidades quando comparado a outros aplicativos, o assim alcunhado “ZeMol” possui menos de 70 kB de memória, e apresenta funcionalidades como:

modelos carregados online do site PDB ou PubChem;
modelos carregados da memória física do dispositivo (formatos PDB, MOL, SDF, XYZ, TXT);
informações de identificação do arquivo PDB (ou nome do arquivo PubChem);
cabeçalho contendo quantitativo de cadeias, ligantes, íons, e ligações dissulfeto;
identificação apenas dos carbonos $\alpha$ de cada resíduo do esqueleto polipetídico, facilitando a visualização do modelo;
visualização automática de ligações dissulfeto;
identificação de resíduos, ligantes, e íons, por hover de mouse sobre o modelo;
checkbox para visualização de estrutura secundária de proteínas (hélice, folha-$\beta$);
checkbox para índice de polaridade dos resíduos;
sliders para tamanho do carbono CA (PDB) ou átomos no geral, e opacidade do modelo (útil pra destaque de fendas, estrutura 2a., cadeia carbônica, ligantes, íons);
ocultar/mostrar partes distintas do modelo, clicando-se em sua legenda (cadeia, íons, hélice/folhas, ligantes);
Destaque de AAs (individual, sequência, todos de um tipo, grupos pré-definidos no script);
HTML autosuficiente no salvamento, “congelando” o modelo nas características que se deseja apresentar;
Zoom em dispositivos móveis (um dedo fixo na tela e outro arrastando o modelo) e Pan (deslocamento do modelo com 2 dedos na tela) - ações também presentes nos ícones acima do modelo;
ajustes facultativos no próprio script (tamanhos, cores, espessuras, grupos de AAs, tipo e espessura de traços, por ex).

Sugestão:

1. Carregue um modelo com código PDB, ou uma molécula do site PubChem;
2. Se proteína, experimente os efeitos separados e combinados dos "sliders" para tamanho do CA e opacidade;
3. Observe a polaridade dos resíduos proteicos no "checkbox" homônimo;
4. Experimente ampliar/reduzir ou deslocá-lo na tela com auxílio do mouse, ou fazê-lo num smartphone conforme a instrução dada acima;
5. Mostre ou esconda alternativamente cada cadeia ou todas, ligantes e íons, clicando-se nos termos respectivos da legenda;
6. Selecione resíduos de interesse do modelo, como sítio catalítico, de ligação a coenzimas, ou de regulação da atividade. Para isso, digite no campo correlato e clique em "destacar". Algumas Sugestão:
  a. Individuais: Arg15, ASP117, 15, A:15, A:ARG15;
  b. Faixas: 15-30, A:15-30, Arg15-Asp30;
  c. Múltiplos separados por vírgula: "Arg15, Asp117";
  d. Grupos: "aromatico", "polar", "apolar", "basico", "acido", "small".

4.3 carbo.Id - Experimentação simulada para caracterização de carboidratos

Contexto:

Assim como apresentado para a caracterização de aminoácidos e cadeias acima, segue uma experimentação simulada para a caracterização de carboidratos. A lógica é a mesma: fornecidos os resultados cromogênicos para reações específicas em tubos de ensaio (gráfico de barras), o usuário busca caracterizar o carboidrato. Isso é feito em relação às reações de:

Teste de Molish - detecta carboidratos (anel púrpura); reação com $\alpha$-naphtol produzindo furfural ou hidroximetilfurfural;
Teste de lugol (I$_{2}$/KI) - detecta polissacarídios (tubo azul escuro);
Teste de Benedict - detecta monossacarídos redutores (e também lactose); tubo com precipitado laranja escuro/tijolo;
Teste de Selliwanoff (resorcinol) - diferencia cetoses (tubo vermelho) de aldoses (tubo rosa fraco);
Teste de Barfoed - diferencia mono (tubo com precipitado vermelho - óxido cuproso) de oligossacarídios (tubo amarelado).

Instruções do simulador

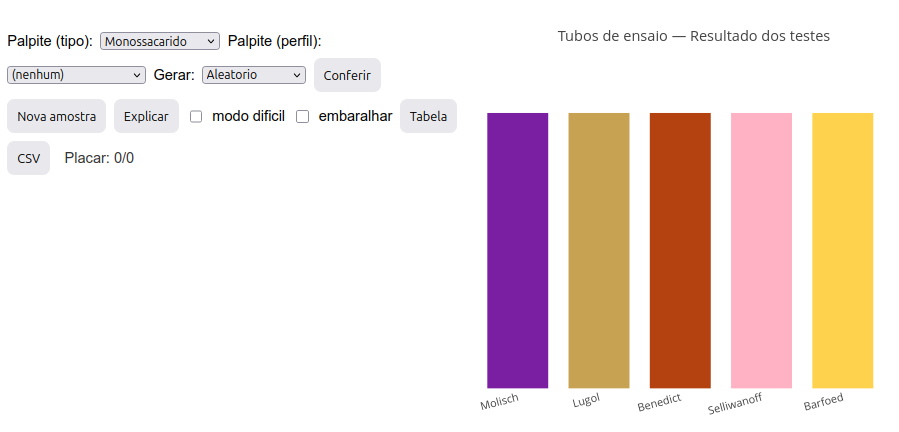
Opção A: descobrir a natureza de uma amostra:

Para descobrir a natureza de uma amostra, siga como no aplicativo para caracterização de aminoácidos e cadeias acima. Para isso:

Clique na imagem abaixo e dê um “add”. Será gerado um conjunto de 5 barras coloridas, representando as cores obtidas em tubos de ensaio para as 5 reações distintas para caracterização de carboidratos: Molish, Lugol, Benedict, Selliwanoff, e Barfoed.
Descubra o tipo de amostra em função do padrão de cores dos tubos apresentado, fornecendo um palpite. O palpite deve ser por tipo (no menu “Palpite (tipo)” - monossacarídio, di-oligossacarídio, polissacarídio, água. E por perfil (no menu “Palpite (perfil)” - redutor, não redutor, aldose, cetose, monossacarídio, di-oligossacarídio, e polissacarídio;
Após a seleção nos 2 menus, clique em “Conferir”. Se tiver acertado, um “Placar” logo abaixo irá computar o número de acertos/número de amostras “jogadas”;
Se errar, tente de novo ou busque a explicação do padrão de cores em “Explicar”;

Existem duas outras possibilidades: “Modo difícil”, que esconde o nome das reações, embora mantendo sua sequência, e “Embaralhar”, que altera a ordem dos tubos;
Para uma nova amostra, basta clicar em “Nova amostra”;

Opção B: descobrir o padrão de cores de uma reação para uma amostra selecionada:

Selecione uma amostra em “Gerar”, e clique em “Nova amostra”. Será gerado um conjunto de tubos com o padrão de reações esperado para a amostra.

Sugestão:

1. Experimente clicar em "Nova amostra" para verificar a frequência de possibilidades;
2. Experimente as duas opções de operação do "simulador/aplicativo/jogo");
3. Experimente o "modo difícil" (sem referência às reações em sequência) ou "embaralhar" (permuta da ordem das reações). Por óbvio, contudo, evite os dois simultaneamente !

4.4 FlowForces

Contexto:

O nome acima remete à alusão do nobelista Ilya Prigogine para processos auto-organizáveis, como os apresentados em células vivas. Nesse caso, as quantidades de determinados reagentes e produtos configuram as forças, enquanto que suas transformações apontam para os fluxos.

Em relação a ambos, por vezes é interessante se estudar o efeito de um modificador, como um ativador ou inibidor, em uma via metabólica ou reação bioquímica qualquer, tanto isoladamente como numa organela, célula, ou mesmo no organismo. Nesse sentido, o aplicativo simula tais efeitos num sistema biológico em que o usuário insere metabólitos em um fluxo contínuo de registro para um sinal arbitrário.

Exemplificando, a adição de modificadores metabólicos numa suspensão celular pode ser monitorada pelo nível de oxigênio da amostra, tal como medido por um oxígrafo, e simulado abaixo.

Sugestão:

1. Experimente alterar um ou mais compostos com embasamento bioquímico, como para uma via metabólica, por exemplo;
2. Teste variações de "delay" para o aparecimento do efeito do modificador clicando-se no checkbox "Avancado";
3. Experimente variar o ruído em "const noise", elevando-o 100x:
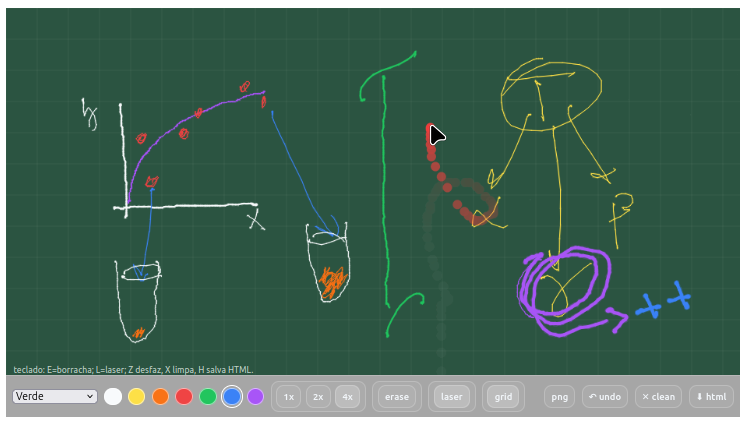
    "const noise = noiseOn ? (Math.random()-0.5)*20"

4.5 Gizz - Lousa Digital

Contexto:

A natureza do objeto abaixo dispensa apresentações. Trata-se mais um entre os muitos aplicativos para simular uma lousa, ou quadro de giz/caneta digital. Diferente de seus concorrentes, contudo:

Pode ser exportada como arquivo autossuficiente HTML em botão da própria lousa, e permitindo compartilhamento da imagem gerada, bem como continuidade de sua edição;
Faculta a personalização do código que o produz, permitindo inserir/alterar canetas, espessuras, e ações distintas não previstas no código-fonte.

Tangente à suas facilidades, a lousa digital permite:

Escrever com 7 cores e 3 espessuras distintas;
Acessar 4 planos de fundo de coloração diferente;
Sobrepor o plano com um grid;
Utilizar um apagador (erase);
Utilizar um apontador laser para localização transiente do que se pretende assinalar;
Salvar a imagem como PNG, indicando data e hora;
Comandos para desfazer (undo) e de limpeza (clean) do quadro;
Atalhos de teclado: E=borracha; L=laser; Z desfaz, X limpa, H salva HTML

Sugestão:

1. Pode-se alterar a espessura das canetas em "var baseWidth = 1;" ;
2. Os botões 1x, 2x, 4x são multiplicadores; edite as linhas de criação dos botões pra trocar rótulo/multiplicador (ex.: "addSize('3x', 3, true)").

5 Toolkits

O JSPlotly pode operar como um aplicativo completo para simulação em situações variadas. As “caixas de ferramentas” que seguem ilustram paineis interativos (dahsboards) para experimentação e análise simulada em Biofísico-química em temas de cinética, interação, e estabilidade para alvos proteicos. Cada toolkit permite uma apreciação entre métodos utilizados, aplicações, modelagem, e interpretação de parâmetros. Como um todo, os toolkits facultam um estudo integrado de cinética e termodinâmica para aplicação em biotecnologia, biocatálise e descoberta de fármacos.

Observações importantes:

Os Toolkits possuem códigos internos para estilos e montagens dos paineis, e que interferem no bootstratp do criador de páginas web utilizado para o Bioquanti (pacote Quarto para R). Nesse sentido, as imagens clicáveis para cada painel remetem aos scripts individuais para carregamento de cada Toolkit no JSPlotly.
Cada painel é apresentado abaixo do ecrã gráfico do JSPlotly. Isso é necessário para maximizar a área para apresentação dos paineis.

Individualmente, os toolkits contemplam:

EK-Toolkit - modelagem em cinética e inibição enzimática;
LeadHunt - prospecção de composto líder por inibição enzimática;
LB-Toolkit - análise de interação ligante-proteína;
GH-Toolkit - estabilidade termodinâmica de biopolímeros;
mTherm-Toolkit - estabilidade sob condições perturbantes;
ThermStab-Toolkit - termoestabilidade enzimática;
Biocel-Toolkit - performance de biocélula a combustível

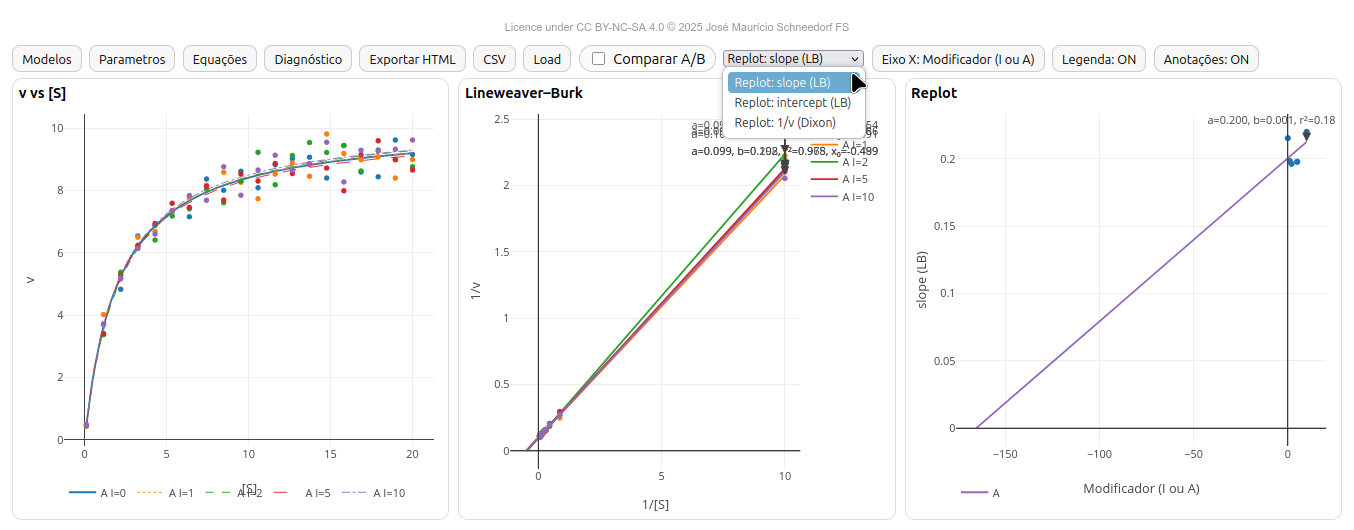
5.1 EK-Toolkit

Instruções gerais

O EK-Toolkit é uma caixa de ferramentas para simulação de cinética e inibição enzimáticas com uso de gráficos diagnósticos. O kit gera três gráficos lado a lado:

Michaelis-Mentem: v × [S];
Lineweaver–Burk (LB) — 1/v vs 1/[S];
Replot - slope ou intercept de LB, ou ordenada de Dixon (1/v)

Recursos adicionais incluem exportação HTML, exportação e carregamento de CSV, anotações editáveis, janelas arrastáveis e comparação de modelos (A/B).

Funcionalidades

Modelos: Michaelis-Menten; Excesso de Substrato; Inibição Irreversível; Inibição Competitiva; Inibição Não-competitiva (pura); Inibição Mista; Inibição Incompetitiva; Bi-substrato (Random Sequential, Ordered Sequential, Ping-Pong); Hill (cooperatividade); Ativação enzimática (Vmax-up); Usuário (equação livre);
Gráficos sincronizados: v×[S], LB (1/v vs 1/[S]) e Replot (slope, intercept ou Dixon 1/v vs modificador);
Comparação A/B com paletas de cores consistentes entre os gráficos;
Painéis: modelos, equações, parâmetros (faixa de [S], número de pontos simulados, erro, modificadores, parâmetros;
Replot configurável com rótulo do eixo X editável.
Ajustes: ajuste linear ponderado em LB e replots - WLS(weighted least squares, peso: 1/y²); OLS (ordinary least squares) em Dixon.
Estimativa de Ki em Dixon; marcador vertical em $x = -K_i$.
Exportação HTML com gráficos interativos e equações; CSV PT-BR (separador ‘;’, decimal ‘,’).
Load de CSV para reconstruir gráficos e diagnóstico; ‘Limpar CSV’ para voltar à simulação.
Modais arrastáveis; anotações clicáveis/editáveis; legenda global ON/OFF.

Modelos

Michaelis–Menten
\[ v = \dfrac{V\_{max} S}{K_m + S} \]

Excesso de Substrato
\[ v = \dfrac{V*{max} S}{K_m + S + \dfrac{S^2}{K*{is}}} \]

Inibição Irreversível
\[ v = \dfrac{V\_{max}(1-f) S}{K_m + S} \]

Competitiva
\[ v = \dfrac{V\_{max} S}{K_m \left(1 + \dfrac{I}{K_i}\right) + S} \]

Não-competitiva (pura)
\[ v = \dfrac{V\_{max}}{1 + \dfrac{I}{K_i}} \cdot \dfrac{S}{K_m + S} \]

Mista
\[ v = \dfrac{V*{max}}{1 + \dfrac{I}{K*{i2}}} \cdot \dfrac{S}{K*m \left(1 + \dfrac{I}{K*{i1}}\right) + S} \]

Incompetitiva
\[ v = \dfrac{V\_{max} S}{K_m + S\left(1 + \dfrac{I}{K_i}\right)} \]

BiBi Random Sequential
\[ v = \dfrac{V\_{max} A B}{K_a K_b + K_a B + K_b A + A B} \]

BiBi Ordered Sequential
\[ v = \dfrac{V\_{max} A B}{K_a K_b + K_b A + A B} \]

BiBi Ping-Pong
\[ v = \dfrac{V\_{max} A B}{K_b A + K_a B + A B} \]

Hill (cooperatividade)
\[ v = \dfrac{V\_{max} S^n}{K^n + S^n} \]

Ativador (Vmax-up)
\[ v = \dfrac{V*{max}\left(1 + \dfrac{A}{K*{aA}}\right) S}{K_m + S} \]

Obs:

a (intercept): valor de 1/v quando 1/[S] = 0.
b (slope): inclinação da reta LB = $Km/V{max}$.
K_i: constante de inibição (Dixon: $x = -K_i$).

Sugestão

1. Experimente comparar o modelo não competitivo puro ao misto; para isso basta igualar ou não, respectivamente, as constantes de inibição;
2. Experimente um modelo introduzido por usuário ("user"). Para isso, basta selecionar Modelos --> User, informar a equação, os parâmetros e seus valores. Segue um exemplo (ativação parcial incompetitiva):

  Equação: (alfa*Vmax*S)/(Km+S*(1+I/Ki))
  Parâmetros: alfa;Km;Vmax;Ki
  Valores: 1.7;2;10;5

Modelos → User, informe Equação (JS), Parâmetros (nomes;) e Valores (;).

Marangoni, Alejandro G. Enzyme kinetics: a modern approach. John Wiley & Sons, 2003.
Purich, Daniel L. Enzyme kinetics: catalysis and control: a reference of theory and best-practice methods. Elsevier, 2010.
Leone, Francisco A. Fundamentos de cinética enzimática. Editora Appris, 2021.
Segel, Irwin H. Enzyme kinetics: behavior and analysis of rapid equilibrium and steady state enzyme systems. Vol. 115. New York: Wiley, 1975.

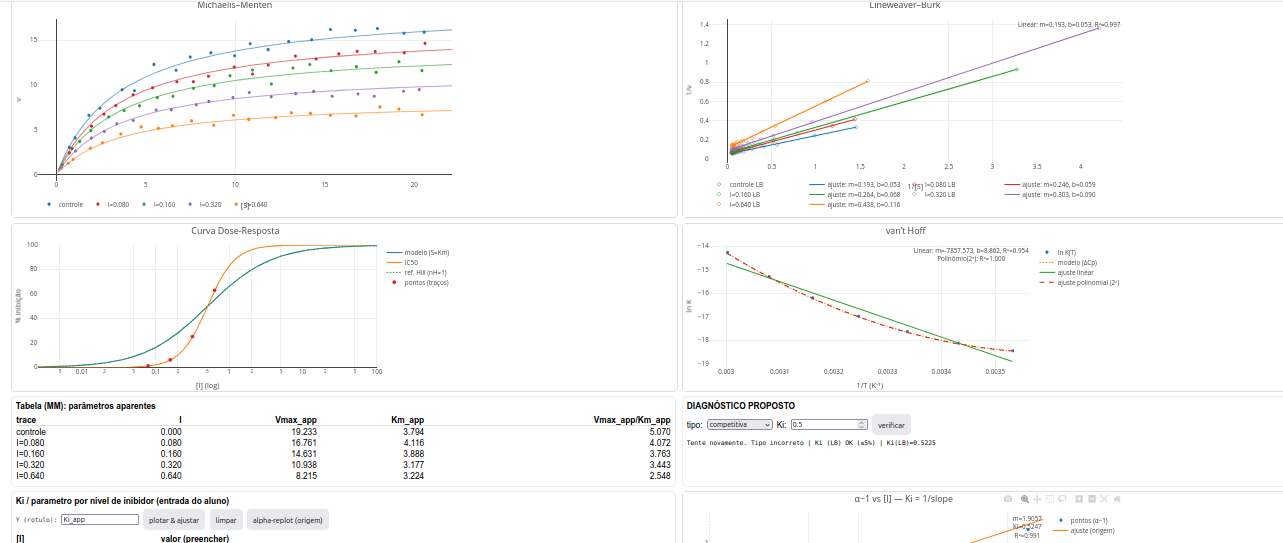
5.2 LeadHunt-Toolkit

O exemplo que se apresenta refere-se ao uso do JSPlotly como um painel (dashboard) para prospecção simulada do potencial de uma molécula fictícia em triagem, visando a seleção de composto líder (lead compound) como inibidor a um alvo enzimático.

Instruções gerais

No campo superior do app há 4 botões:

reset - renova a simulação para outros dados e gráficos;
html - salva os gráficos e dados em arquivo interativo;
diagnóstico - abre janela popup para o diagnóstico do modelo de inibição e valores de parâmetros;
parâmetros - abre janela para simulação gráfica frente a parâmetros do usuário.

Há dois modos para estudo para uso do LeadHunt: inserindo-se parâmetros cinéticos e termodinâmicos para observar os resultados expressos em gráficos (botão parâmetros), ou caracterizar os parâmetros a partir dos gráficos (botão diagnóstico).

Os gráficos simulam os resultados obtidos para as representações de Michaelis-Mentem, Lineweaver-Burk, curva dose-reposta, e gráfico de van’t Hoff.

Parâmetros

Seja qual for o modo experimentado, se para identificar o potencial do composto , os parâmetros são:

Ki, constante de equilíbrio de dissociação do inibidor (desejável < 10$\mu$M);
Vmax, velocidade limite da reação enzimática;
Km, constante de Michaelis-Mentem;
$\Delta$H, variação de entalpia de ligação com inibidor;
$\Delta$S, variação de entropia de ligação com inibidor;
$\Delta$Cp, variação de capacidade calorífica da ligação com inibidor;

Além desses parâmetros, a molécula fictícia conta com alguns descritores, a saber:

MW, peso molecular;
HAC, número de átomos pesados (todos, exceto hidrogênio);
HBD, número de doadores de ligação de H;
HBA, número de aceptores de ligação de H;
logP, logaritmo do coeficiente de partição da molécula

Esses descritores permitem o cálculo para outros critérios visando a seleção de líder:

LE, eficiência de ligante (ligand efficiency):
\[ LE = \frac{\Delta G}{HAC}; \]

\[ LE = 1.37 \frac{pIC_{50}}{HAC} \]

Onde pIC$_{50}$ = -log(IC$_{50}$);

LLE, eficiência lipofílica do ligante (lipophilic ligand efficiency; valores >5 são considerados bons),

\[ LLE=pIC_{50}-logP \]

BEI, índice de eficiência da ligação (binding efficiency index),

\[ BEI=\frac{pIC_{50}}{MW} \]

Onde: MW, kDa; faixas típicas pela regra de Lipinski (regra dos 5): MW<=500, HBD<=5, HBA<=10, cLogP<=5. E também LE >= 0.3; LLE >= 5.

Já a curva dose-reposta do inibidor permite a determinação de:

IC$_{50}$, concentração do inibidor que confere 50% de resposta (adequado quando < 10$\mu$M);
nH, constante de Hill (índice de cooperatividade)

Uso do LeadHunt para identificação de um composto líder

A partir da visualização de gráficos e descritores da molécula fictícia, é possível se determinar:

O tipo de inibição reversível (competitiva, incompetitiva, não competitiva pura, não competitiva mista);
O valor de Ki por construção de gráficos secundários variados a partir da tabela de preenchimento de parâmetros (Tabela para Ki) - plota-se a concentração I do inibidor versus Km, Vm, ou Km/Vm aparentes. Alternativamente, plota-se I contra o valor de ($\alpha$-1), onde $\alpha$ representa “1+I/Ki”;
O valor de IC$_{50}$ e de nH (inclinação do ponto médio) pela curva de dose-resposta do inibidor (estimativa de cooperatividade na ligação);
O valor de $\Delta$H e $\Delta$S para o plot de Van’t Hoff. No caso em que o gráfico apresentar-se curvilinear, também o valor valor de $\Delta$Cp;
Os valores de LE e LLE;
Avaliar o candidato junto às regras de Lipinski.

Dessa forma, pode-se utilizar o LeadHunt para uma simulação significativa à triagem de um inibidor como lead compound à uma enzima-alvo.

Sugestão

1. Compare os tipos de inibição enzimática por inspeção visual dos gráficos de Michaelis-Mentem e de Lineweaver-Burk, dando ênfase às variações ou não de "Km" e "Vmax" entre esses;

2. Calcule o valor de "Ki" por métodos distintos utilizando-se o campo de preenchimento para "replot" por nível de inibidor (tabela de "Parâmetros aparentes"):
    a) obtendo-se o valor de "1/Ki" para plot de I x (alfa-1) do botão "alfa-replot" (inclinação da reta);
  b) por intercepto "-Ki" a partir de plots de I x Vm_app, Km_app, ou Km/Vm_app (dependendo do modelo de inibição);
  c) por "inclinação" ou "intercepto" de replots de Lineweaver-Burk contra I

3. Experimente o modo "parâmetros" com valor de "nH" diferente de 1 (ex: 2,8), para avaliar o comportamento da curva dose-reposta sob efeitos de cooperatividade;

4. Experimente o modo "parâmetros" com valor para capacidade calorífica diferente de zero (ex: -2000), para avaliar a possibilidade de efeitos secundários na ligação em função da temperatura, como transição conformacional da enzima;

5. Teste a curvatura do plot de Van´t Hoff para variação de capacidade calorífica da interação, fornecendo valores positivos (ex: 2000) e negativos (ex: -2000): se concavidade para cima, valor negativo da variação de capacidade calorífica; se concavidade para baixo, valor positivo.

Referências:

Marangoni, Alejandro G. Enzyme kinetics: a modern approach. John Wiley & Sons, 2003.
Copeland, Robert A. Evaluation of enzyme inhibitors in drug discovery: a guide for medicinal chemists and pharmacologists. John Wiley & Sons, 2013.
Copeland, Robert A. Enzymes: a practical introduction to structure, mechanism, and data analysis. John Wiley & Sons, 2023.
Leone, Francisco A. Fundamentos de cinética enzimática. Editora Appris, 2021.

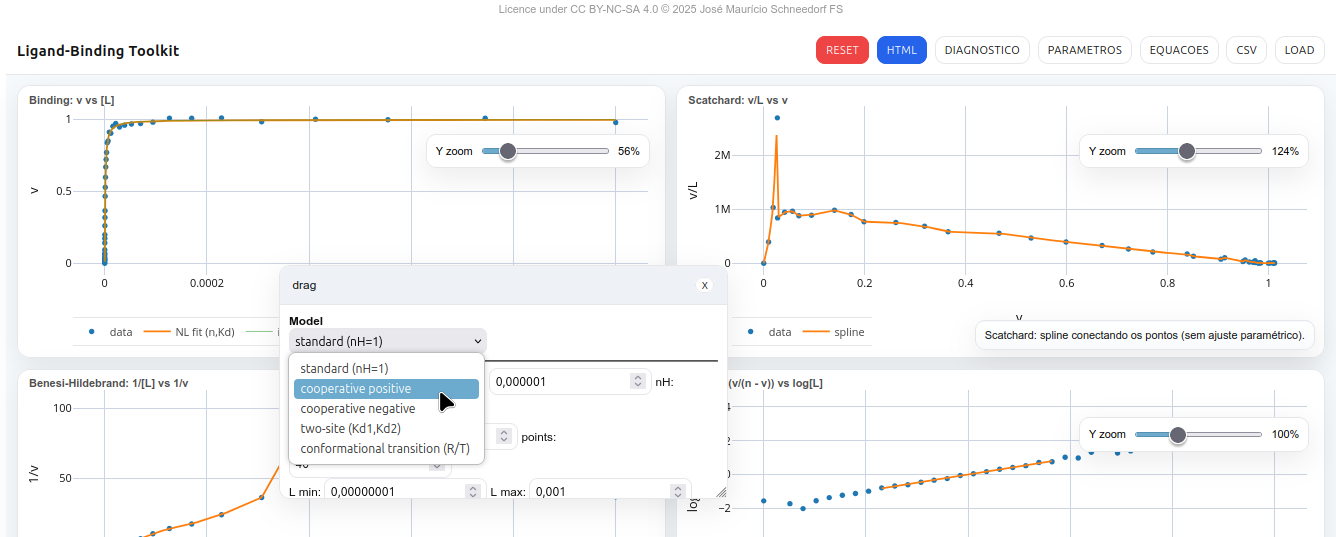
5.3 LB-Toolkit

Instruções gerais

O LB-Toolkit é um painel interativo para análise de ensaios de ligação ligante–receptor (proteína, enzima, ácido nucleico, glicano). Permite visualizar e ajustar curvas clássicas de ligação (Binding, Scatchard, Benesi–Hildebrand e Hill), e acompanha exportação HTML interativa de dados e gráficos.

Funcionalidades

O LB-Toolkit permite estudo e visualização gráfica de um painel 2 x 2 representativo dos modelos clássicos de interação bimolecular de Langmuir, Hill (cooperatividade positiva e negativa), heterogeneidade de sítios (two-site), e de transição conformacional (R/T). A exportação HTML é autossuficiente, e a importação/exportação para arquivos CSV dá-se por vetores L,v.

As funções principais da barra superior são: RESET (restaura valores padrão), HTML (exporta viewer autônomo), DIAGNOSTICO (mostra um resumo do modelo), PARAMETROS (abre painel de controle), EQUACOES (exibe fórmulas dos modelos), e CSV/LOAD (exporta ou importa dados em formato L,v.

Parâmetros ajustáveis

n, Kd, nH, erro sigma, points, Lmin, Lmax
Two-site: n1, n2, Kd1, Kd2
Conformational (R/T): Kt, KdR, KdT
Toggles: draw model only, results below, Hill 10–90%, zoom sliders, autoplot

Modelos

Langmuir

\[ v = n\,\frac{[L]}{K_d + [L]} \]

Hill

\[ v = n\,\frac{[L]^{n_H}}{K_d^{n_H} + [L]^{n_H}} \]

Linearização:

\[ \log\!\left(\frac{v}{n - v}\right) = n_H \log[L] - n_H \log K_d \]

Two-site (heterogeneidade de sítios)

\[ v = n_1\,\frac{[L]}{K_{d1} + [L]} + n_2\,\frac{[L]}{K_{d2} + [L]} \]

Conformational (R/T)

\[ v = n\,\frac{L/K_{dR} + K_t L/K_{dT}}{1 + L/K_{dR} + K_t(1 + L/K_{dT})} \]

Linearizações clássicas

Os ajustes são exibidos como linhas spline suaves, pois os parâmetros de uma regressão polinomial não têm significado físico direto.

Scatchard

\[ \frac{v}{[L]} = \frac{n}{K_d} - \frac{1}{K_d} v \]

Benesi–Hildebrand

\[ \frac{1}{v} = a\,\frac{1}{[L]} + b \]

Ajustes e estimativas

Binding (n,Kd): ajuste não linear (Gauss–Newton).
Scatchard e Benesi: interpolação spline visual.
Hill: regressão linear 10–90 %.

5.3.0.1 Gráficos

Binding: v vs [L] – curva teórica + pontos experimentais.
Scatchard: v/L vs v – linha spline ajustada aos dados.
Benesi–Hildebrand: 1/[L] vs 1/v – spline ilustrativo.
Hill: log(v/(n–v)) vs log[L] – regressão linear com exibição de nH e Kd.

Sugestão

1. Utilize o "slider" (barra de deslizamento) para ampliação/redução dos gráficos;
2. Experimente personalizar as represetações gráficas. Ilustrando, clique no botão "Parâmetros" e altere o modelo para cooperatividade negativa com dois sítios, atribuindo valores distintos a esses (opcional).

Referências

Carey, Jannette. Ligand-Binding Basics: Evaluating Intermolecular Affinity, Specificity, Stoichiometry, and Cooperativity. John Wiley & Sons, 2025.
Roque, Ana Cecília A. “Ligand-Macromolecular interactions in drug discovery.” Clifton, NJ 2010; p 572 (2010).
Mannhold, Raimund, Hugo Kubinyi, and Gerd Folkers. Protein-ligand interactions: from molecular recognition to drug design. John Wiley & Sons, 2006.
Klotz, Irving. Introduction to biomolecular energetics: including ligand–receptor interactions. Elsevier, 2012.

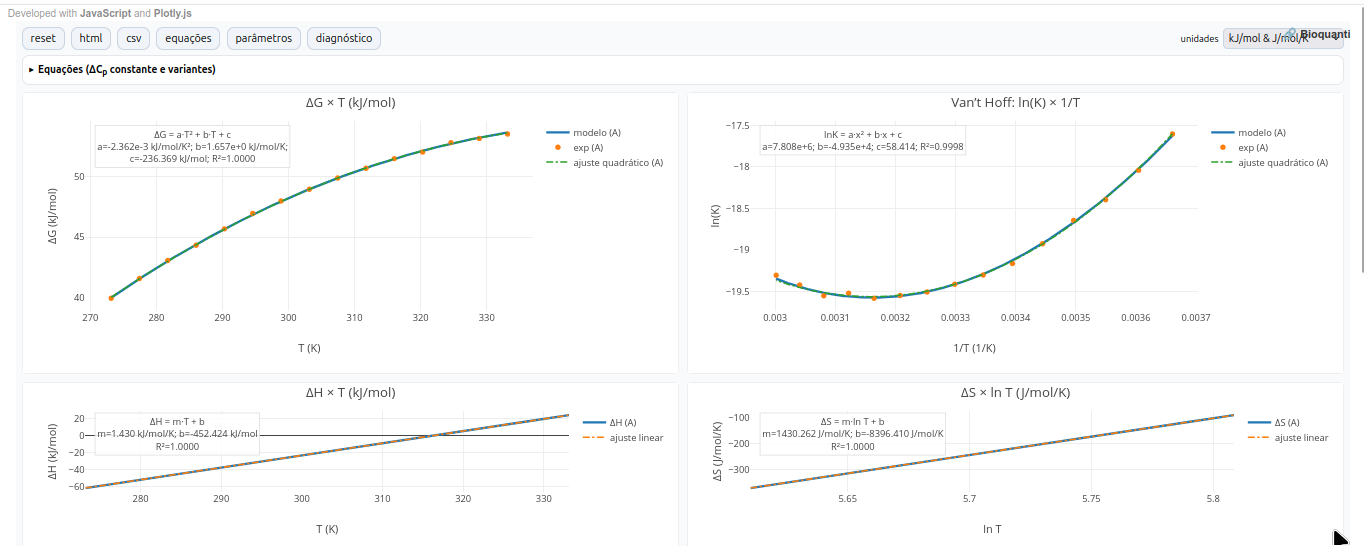
5.4 GH-Toolkit

Instruções gerais

Este toolkit apresenta algumas relações de Gibbs–Helmholtz e de Van’t Hoff observadas no estudo de termodinâmica de proteínas e interações macromoleculares envolvendo folding, unfolding e ligand-binding com ΔCₚ constante (e uma variante simples com ΔΔCₚ). Inclui formas úteis para simulação a partir de parâmetros em T₀ ou em Tₘ, além de linearizações diagnósticas para leitura direta de parâmetros.

O simulador permite trabalhar-se com equações fundamentais (formas em $T_0$ e centrada em $T_m$) com $ΔC_p$ constante e variante linear. A interpretação dos ajustes (regressões) é apresentada graficamente, a partir dos Parâmetros selecionados. São também incluidos alguns Cenários para comportamento (mesófilo, psicrófilo, termófilo), bem como Presets para quantidades termodinâmicas. O app permite simular valores de ΔG(T) diretamente a partir de $(T_m,\,ΔH_m,\,ΔC_p)$, e exporta gráficos e dados (CSV/HTML) em unidades selecionáveis (kJ/mol ↔︎ kcal/mol; J/mol/K ↔︎ cal/mol/K).

Parâmetros

1. Forma com referência em $T_0$ (integrais com $ΔC_p$ constante)

Entalpia

\[ ΔH(T)=ΔH^\circ + ΔC_p\,(T-T_0) \]

Entropia

\[ ΔS(T)=ΔS^\circ + ΔC_p\ln\!\left(\frac{T}{T_0}\right) \]

Energia de Gibbs (Gibbs–Helmholtz integrada)

\[ ΔG(T)=ΔH^\circ - T\,ΔS^\circ + ΔC_p\Big[(T-T_0)-T\ln\!\left(\frac{T}{T_0}\right)\Big] \]

Constante de equilíbrio

\[ \ln K(T)= -\frac{ΔG(T)}{R\,T} \]

2. Forma centrada em $T_m$ (curva de estabilidade por $ΔH_m$ e $ΔC_p$)

Esta forma é conveniente quando se conhece a temperatura de equilíbrio $T_m$ (onde $ΔG=0$), a variação de entalpia em $T_m$ ($ΔH_m$) e $ΔC_p$:

\[ ΔG(T)=ΔH_m\!\left(1-\frac{T}{T_m}\right) + ΔC_p\Big[(T-T_m)-T\ln\!\left(\frac{T}{T_m}\right)\Big]. \]

A partir desta expressão é possível obter-se retroativamente parâmetros em $T_0$ coerentes com a curva:

\[\begin{aligned} ΔH^\circ(T_0) &= ΔH_m + ΔC_p\,(T_0-T_m),\\[4pt] ΔS^\circ(T_0) &= \frac{ΔH_m}{T_m} + ΔC_p\ln\!\left(\frac{T_0}{T_m}\right). \end{aligned}\]

No app, o botão “gerar por Eq. $T_m$” aplica estas relações.

3. Capacidade calorífica com variação linear (termo $ΔΔC_p$)

Para explorar pequenas variações lineares de capacidade calorífica em torno de uma referência $T_r$:

\[ C_p(T)=C_{p,r}+ΔΔC_p\,(T-T_r). \]

No app, marcar “Comparar duas proteínas (usar $ΔΔC_p$)” plota a proteína B com $ΔC_{p,B}=ΔC_{p,A}+ΔΔC_p$ e mostra a consequência na curvatura de $ΔG(T)$ e no deslocamento de $T_m$.

Cenários

O Cenário escolhe a natureza do processo modelado e inicializa sinais e ordens de grandeza coerentes:

Folding exotérmico: $ΔH^\circ<0$; estabilização entálpica dominante a $T_0$.
Folding endotérmico: $ΔH^\circ>0$ e $ΔS^\circ>0$ (ganho entrópico compensa).
Unfolding: inverte os sinais de folding.
Binding exotérmico / endotérmico: ajustes típicos para interação ligante–receptor.

Sugestão

1. Orientação: T_m ocorre quando ΔG=0. Nesse caso, é mostrada uma linha vertical tracejada no gráfico ΔG x T;
2. Selecione um "Preset" didático e compare o efeito nas curvas de estabilidade:
  - Nenhum: sorteio coerente.
  - termo ↑ΔG global: torna ΔS mais negativo (eleva ΔG globalmente).
  - termo ↓ΔC_p: achata a curvatura em ΔG(T).
  - psicro ↑ΔC_p: acentua a curvatura.
  - binder ΔC_p<0: usa ΔC_p negativo (casos de ligação hidrofóbica reduzida etc.).
3. A curvatura de ΔG(T) cresce com |ΔC_p|; assim, compare A vs B, e veja a diferença no perfil gráfico ("shape") e no deslocamento de T_m;
4. Observe que:
  - a representação de Van’t Hoff recupera ΔH e ΔS (quando ΔC_p = 0).rve que
  - slopes/interceptos: servem de checagem de consistência entre gráficos
  - de ΔH x T: slope permite ΔC_p.
  - De ΔS x ln T: slope permite ΔC_p, e intercepto compatível com ΔS e T_0.

Referências

Atkins, Peter William, et al. Physical chemistry for the life sciences. Oxford University Press, 2023.
Hammes, Gordon G. Thermodynamics and kinetics for the biological sciences. John Wiley & Sons, 2000.
Cooper, Alan. Biophysical chemistry. No. 24. Royal Society of Chemistry, 2011.
Creighton, T. The Biophysical Chemistry of Nucleic Acids & Proteins. Helvetian Press, 2010.

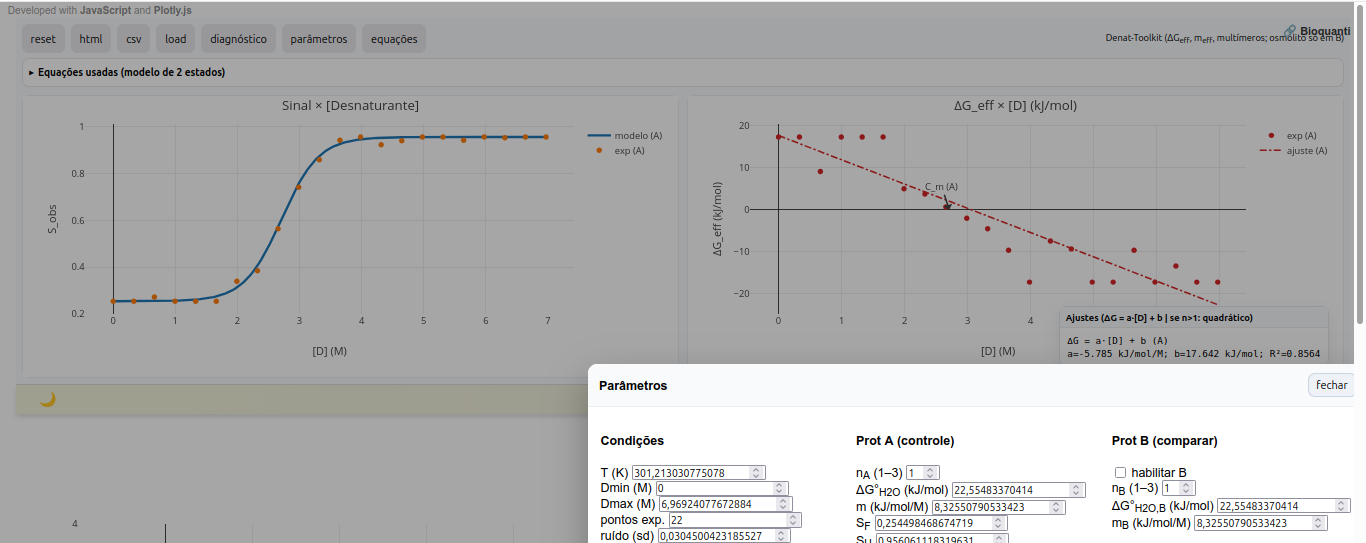
5.5 mTherm-Toolkit

Instruções gerais

O toolkit constitui um app educacional para simular os perfis gráficos de desnaturação de proteínas (ex.: ureia, GdnHCl), e com suporte a proteínas multiméricas e um termo empírico para uso de osmólitos. Os dados são plotados em função de um sinal experimental (absorvância/fluorescência), seguindo-se o cálculo de frações conformacionais e energia de Gibs efetiva em função do desnaturante. O simulador também permite comparação entre proteínas ou condições experimentais (A/B).

O app trabalha com modelo de dois estados entre um conjunto “nativo” (F) e outro “desnaturado” (U). O efeito do desnaturante é linear sobre a energia padrão do monômero (LEA – Linear Extrapolation Assumption). Para simulação de um osmólito (estabilizante ou não) utiliza-se um termo empírico multiplicativo na inclinação (m).

Complementarmente, o simulador permite a exportação de figuras interativas e de seu diagnóstico (HTML), exportação CSV para dados de desnaturante, sinal e variação de energia juntamente ao diagnóstico, bem como presets de interface JSON para cenários (salvar/carregar).

Parâmetros

Energia padrão vs. ([D]) — monômero (LEA)

\[ \Delta G^\circ(D)=\Delta G^\circ(\mathrm{H_2O})-m\,D \tag{2.1} \]

Multímero (F_n nU) — lei de massa (resolver (f_U))

\[ \Delta G^\circ + RT\ln\!\left(\frac{n\,f_U^{\,n}}{P_t^{\,n-1}(1-f_U)}\right)=0 \tag{2.2} \]

(n): número de monômeros em (F_n);
(Pt): concentração de _monômero equivalente (em M);
A Eq. (2.2) é resolvida numericamente (bissecção) para (0<f_U<1) em cada (D);

Energia livre efetiva

\[ \Delta G_{\mathrm{eff}}(D)=-RT\ln\!\left(\frac{f_U}{1-f_U}\right) \tag{2.3} \]

Inclinação efetiva (m_{}) (dependente de (D))

\[ m_{\mathrm{eff}}(D) = \frac{m}{\,n + (1-n)\, f_U(D)\,}\quad \left(\approx \frac{m}{n}\ \text{no lado nativo; } \approx m \text{ no lado desnaturado}\right) \tag{2.4} \]

Intercepto nativo efetivo em água (aproximação para multímeros)

\[ \Delta G_{\mathrm{eff}}(\mathrm{H_2O}) \approx \frac{\Delta G^\circ(\mathrm{H_2O})}{n} + \frac{RT}{n}\ln n - RT\!\left(1-\frac1n\right)\!\ln P_t \tag{2.5} \]

Osmólitos

Osmólitos tendem a aumentar a estabilidade frente ao desafio de desenaturantes. O simulador permite observar o efeito de osmólitos compatíveis (ex.: glicina, sorbitol, sacarose, betaína) nos gráficos resultantes. No app é modelado um efeito empírico e simples como uma escala na inclinação:

\[ m_{\mathrm{eff}} = m \,\bigl(1 + k_{\mathrm{osm}}\,[\mathrm{osm}]\bigr) \tag{6.1} \]

onde (k_{}) é um parâmetro de força ajustável (típicamente 0.05–0.2 M$^{-1}$). Esse termo desloca a curva sem impor um mecanismo específico, permitindo exploração didática.

Ajustes e Parâmetros

Temperatura (T) (K) e (P_t) (µM, equivalente de monômero);
Energia em água ($\Delta$G$^{H_2O}$) e inclinação (m);
Multiplicidade (n): (1 n ) para A e, independentemente, para B;
Sinais de base (S_F, S_U) e ruído;
Comparação A/B: segunda proteína pode ter (n), (m), $\Delta$G$^{o}$, e osmólito diferentes.

Sugestão

1. Obseve a curvatura do gráfico em ΔG x [D]. Valores de n>1 sugerem um estado multimérico para o biopolímeros;
2. Veja que o "ponto médio*" de C_m, onde f_U é aproximadamente 0,5, é marcado no diagnóstico para referência;
3. Compare o efeito de osmólito comparando-se proteínas ou condições A e B, alterando-se a concentração do osmólito e sua constante empírica "k_osm".

Referências

Park, Chiwook, and Susan Marqusee. “Analysis of the stability of multimeric proteins by effective ΔG and effective m‐values.” Protein science 13.9 (2004): 2553-2558.
Holthauzen, Luis Marcelo F., et al. “Protein stability in the presence of cosolutes.” Methods in Enzymology. Vol. 492. Academic Press, 2011. 61-125.
Scholtz, J. Martin, Gerald R. Grimsley, and C. Nick Pace. “Solvent denaturation of proteins and interpretations of the m value.” Methods in enzymology. Vol. 466. Academic Press, 2009. 549-565.

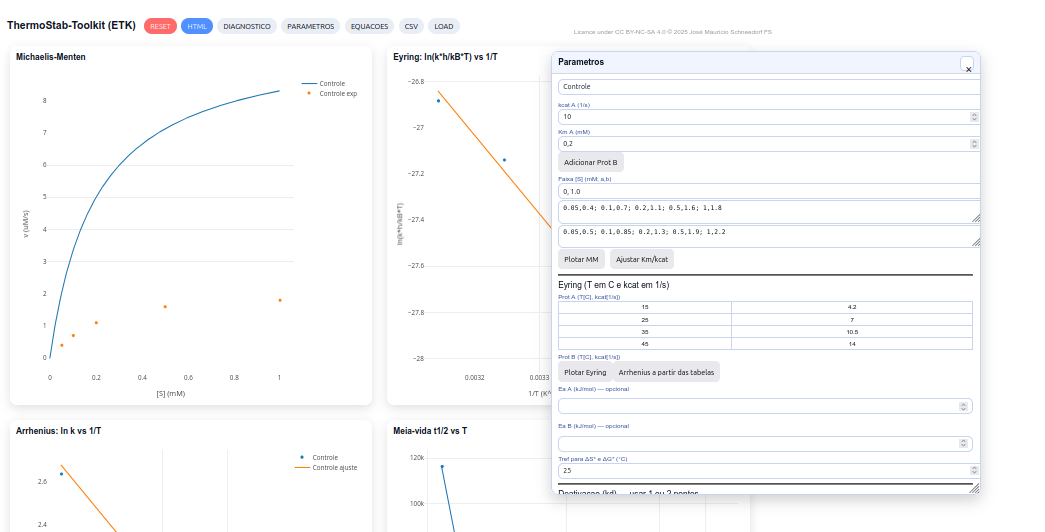
5.6 ThermStab - Toolkit

Instruções gerais

O toolkit é apresentado como um painel didático e interativo em para se explorar parâmetros termo-cinéticos de estabilidade correlatos à atividade enzimático. Aborda algumas relações de Michaelis–Menten (MM), Eyring, Arrhenius e curvas de meia-vida (t$_{1/2}$). Como outros kits apresentados, suporta duas proteínas (A/B), exporta HTML com os gráficos e CSV do estado. Também permite a estimação de valores de Km e k$_{cat}$ por ajuste não-linear.

Parâmetros

Michaelis–Menten (MM)

\[ v = \frac{V_{\max}[S]}{K_m + [S]} \]

\[ V_{\max} = k_{\text{cat}} \cdot E_0 \qquad (E_0 = 1.0\ \mu\text{M}) \]

Relações termodinâmicas associadas:

\[ \Delta G^{\ddagger}_{ES} = -RT \ln \left(\frac{1}{K_m}\right) \]

\[ \Delta G^{\ddagger}*{ET} = -RT \ln \left(\frac{k*{\text{cat}}}{K_m}\right) \]

Equação de Eyring

\[ \ln \left(\frac{k h}{k_B T}\right) = -\frac{\Delta H^{\ddagger}}{RT} + \frac{\Delta S^{\ddagger}}{R} \]

\[ \Delta G^{\ddagger} = \Delta H^{\ddagger} - T\Delta S^{\ddagger} \]

Equação de Arrhenius

\[ \ln k = -\frac{E_a}{RT} + \ln A \]

Meia-vida Enzimática

\[ t_{1/2} = \frac{\ln 2}{k_d} \]

Equilíbrio de ligação

\[ K_d = \frac{[E][S]}{[ES]} \]

\[ \ln K_d(T) = -\frac{\Delta H^\circ}{RT} + \frac{\Delta S^\circ}{R} \]

Relações cinéticas

\[ K_m \approx \frac{k_{-1} + k_{\text{cat}}}{k_1} \]

\[ K_d \approx \frac{k_{-1}}{k_1} \]

\[ k_{-1}(T) \approx k_1,K_d(T) \]

Relação entre estabilidade e catálise

\[ k_d(T) \approx k_1 K_d(T) - k_{\text{cat}}(T) \]

\[ t_{1/2}(T) = \frac{\ln 2}{k_d(T)} \]

Aproximação didática

\[ \ln t_{1/2} \approx \frac{\Delta H^\circ}{R}\left(\frac{1}{T}\right)* \frac{\Delta S^\circ}{R} + \text{constante} \]

Sugestão

1. Utilize o botão RESET e discuta a forma da curva MM e a influência de Km e kcat;
2. Explore as relações de Eyring e de Arrhenius para se obter ΔH‡, ΔS‡, ΔG‡ e Ea, a partir de slopes e interceptos dos gráficos;
3. Explore o efeito da temperatura e compare com modo livre (t₁/₂)m aula.

Referências

Bhatti, Haq Nawaz, et al. “Effect of aniline coupling on kinetic and thermodynamic properties of Fusarium solani glucoamylase.” Applied microbiology and biotechnology 73.6 (2007): 1290-1298.
Lonhienne, Thierry, Charles Gerday, and Georges Feller. “Psychrophilic enzymes: revisiting the thermodynamic parameters of activation may explain local flexibility.” Biochimica et Biophysica Acta (BBA)-Protein Structure and Molecular Enzymology 1543.1 (2000): 1-10.

5.7 Biocel-Toolkit

Instruções gerais

O toolkit aborda um simulador que permite visualizar a operação de uma célula a combustível microbiana (MFC — Microbial Fuel Cell) sob o modelo simplificado de Thevenin. Seu objetivo é auxiliar na compreensão física e termodinâmica da performance de uma célula a combustível (MFC, ou bateria simples), a partir das relações entre tensão, corrente, potência e resistência interna da célula.

O simulador também inclui o impacto de modificadores bioquímicos e variações experimentais como a maturação do biofilme, a depleção de substrato, e overshooting observados em condições reais de operação.

Como para os tookits anteriores, parte a interatividade cedida pelo simulador permite exportar e reimportar dados experimentais (CSV/JSON), e gerar um arquivo autossuficiente com gráficos interativos e diagnósticos (Salvar HTML), e reinicializar para uma nova configuração (Reset),

Parâmetros

Modelo de Thevenin

O circuito equivalente da célula microbiana é modelado como uma fonte de tensão $E_{OCV}$ (tensão de circuito aberto) associada a uma resistência interna $R_{int}$ e a uma resistência externa $R_{ext}$, conforme o teorema de Thevenin.

A corrente $I$ e a tensão no resistor de carga $V$ são dadas por:

\[ I = \frac{E_{OCV}}{R_{int} + R_{ext}}, \qquad V = I \, R_{ext} \]

Potência Elétrica e Condição de Máximo

A potência instantânea dissipada na carga é dada por:

\[ P = E_{OCV} \, I - R_{int} I^2 \]

Substituindo a expressão de $I$ pelo modelo de Thevenin:

\[ P = \frac{E_{OCV}^2 \, R_{ext}}{(R_{int} + R_{ext})^2} \]

O ponto de máxima potência ocorre quando $R_{ext} = R_{int}$, conhecido como condição de Jacobi, e resulta em uma potência máxima de:

\[ P_{\text{máx}} = \frac{E_{OCV}^2}{4 R_{int}} \]

Sobretensões de Ativação e Concentração

Para representar os fenômenos eletroquímicos de ativação e difusão de massa, o potencial observado ($V_{pol}$) é reduzido por dois termos de perda:

\[ V_{pol} = V_{lin} - \eta_{act} - \eta_{conc} \]

onde:

\[ \eta_{act} = A \ln\!\big(1 + \frac{I}{I_0}\big), \qquad \eta_{conc} = C \, \frac{(I/I_{lim})^2}{1 - I/I_{lim}} \]

Essas relações simulam as quedas de potencial associadas à cinética eletroquímica e à limitação de transporte de íons e substratos.

Dinâmica Temporal

Durante a operação, a célula apresenta uma variação de potencial e resistência interna em função do tempo, representadas por:

\[ E_{OCV}(t) = E_{\max}\big(1 - e^{-k_{act}t}\big) s(f) \]

\[ R_{int}(t) = R_0 \big(1 + \beta (1 - f)\big) \]

Onde:

\[ s(f) = 0.40 + 0.60f, \quad f = \frac{Q}{Q_{teor}} \]

Essas funções descrevem a ativação progressiva do biofilme e a modulação resistiva devido à depleção de substrato.

Cargas e Eficiências

A carga teórica disponível na biocélula é dada por:

\[ Q_{teor} = n_{\text{gluc}} \, n_e \, F \]

Onde: $F$ é a constante de Faraday e $n_e = 24$ o número de elétrons por mol de glicose.

A eficiência de carga ($\eta_Q$) e a eficiência energética ($\eta_E$) são calculadas por:

\[ \eta_Q = 100 \times \frac{\int I\,dt}{Q_{teor}} \quad [\%] \]

\[ \eta_E = 100 \times \frac{\int IV\,dt}{Q_{teor} E_{\max}} \quad [\%] \]

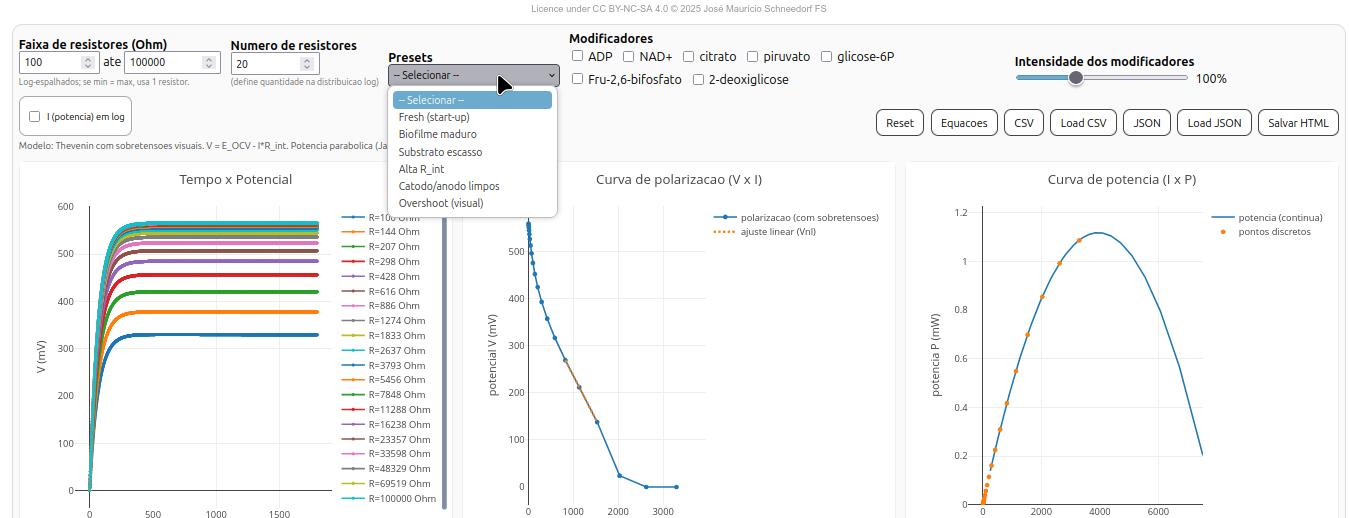
Interface e Funcionalidades

A interface do BioFuelCell é dividida em três painéis gráficos e uma seção de parâmetros:

Tempo × Potencial (t × V) — mostra a evolução do potencial de saída ao longo do tempo para cada resistor externo;
Curva de Polarização (V × I) — apresenta o decaimento de tensão em função da corrente, com ou sem sobretensões;
Curva de Potência (I × P) — calcula a potência dissipada na carga e destaca o ponto de máxima potência.

Abaixo dos gráficos, são exibidos parâmetros calculados automaticamente:

$R_{int,lin}$ — resistência interna pelo ajuste linear da curva real;
$R_{int,ideal}$ — resistência interna teórica (modelo de Thevenin);
$P_{\max}$ e $R_{P\max}$ — potência máxima e resistência correspondente;
$\eta_Q$ e $\eta_E$ — eficiências de carga e energia.

5.7.1 Parâmetros e Modificadores

O usuário pode ajustar:

Faixa de resistores — mínimo e máximo de $R_{ext}$ (em Ω), distribuídos logaritmicamente;
Intensidade dos modificadores — de 0 % a 300 %;
Escala logarítmica da potência — alterna o eixo de corrente em escala log;
Presets experimentais — condições simuladas pré-definidas.

Sugestão

1. Observe o ponto de interseção entre a curva de polarização e a parábola ideal. Esse ponto indica o equilíbrio entre fornecimento e consumo de elétrons;
2. Note a inclinação inicial da curva V×I, e que representa o valor da resistência interna (R_int) da biocélula;
3. Verifique a eficiência interna do sistema, por observação da posição do pico no gráfico de potência;
4. Experimente o perfil das curvas com alguns dos "Presets" experimentais (biofilme maduro, excesso de substrato, etc), e avalie o efeito das condições no desempenho eletroquímico apresentado nos gráficos e resultados.

Deverá aparecer o gráfico de potencial X tempo.

Referências

Logan, B. E. Microbial Fuel Cells. John Wiley & Sons, 2008.
Bard, A. J., & Faulkner, L. R. Electrochemical Methods: Fundamentals and Applications. Wiley, 2022;
Silveira, G., & Schneedorf, J. M. “Evaluation of kefir as a new anodic biocatalyst consortium for microbial fuel cell.” Applied Biochemistry and Biotechnology, 185(4), 1118–1131 (2018).

6 Arduino & Biocélula

Visando ilustrar o potencial do JSPlotly para além do mundo virtual, o exemplo a seguir apresenta uma aplicação experimental para JSPlotly adaptado à aquisição de dados de uma biocélula a combustível por placas microcontroladoras, como Arduino e ESP32, e tal como exemplificado virtualmente no Biocel-Toolkit acima.

O interfaceamento pode ser obtido por uma conexão WebSerial a um Arduino por meio de cabo serial USB (abaixo), bem como por recursos de IoT (“Internet das Coisas”) por meio de Bluetooth/Wifi.

6.1 Cabo Serial

O código é adaptado para uso autônomo, bastando-se conectar o Arduino com um cabo serial USB à placa interfaceada em notebook/PC, seguindo-se o botão Conectar. Segue a lista de arquivos necessários para a reprodução do experimento:

O arquivo de procedimentos detalha a conexão do Arduino por cabo serial para notebook/desktop, somente com firmware Arduino como também pelo software HTML, assim como por Wifi (Android/IOS).

"** DICA RÁPIDA ** ":

  1. Conectar a placa Arduino;
  2. Abrir um CMD ou Terminal e digitar:
   "python3 -m http.server" ;
  3. Carregar o sketch;
  4. Abrir o software no Chrome (Firefox é problemático)
  5. Conectar a porta do Arduino no software

6.2 Internet das Coisas - IoT

O experimento ilustrado acima pode ser conduzido também junto a módulos para conexão Bluetooth ou Wifi presentes em algumas placas microcontroladoras, permitindo expandir-se ainda mais as aplicações práticas do simulador e da biblioteca Plotly.js para uso com tablets e celulares. A imagem que segue ilustra um experimento conduzido com biocélula a combustível, e interfaceada por rede Wifi para uma placa Arduino Uno R4 Wifi.

Para uso com rede Wifi é necessário utilizar-se este sketch Arduino-Wifi específico para a Biocélula.

"** DICA RÁPIDA ** ":
  1. Conectar a placa Arduino;
  2. Carregar o sketch;
  3. Abrir o Serial Monitor;
  4. Opcional: apertar Reset por ~2s no Arduino;
  5. Acessar a rede específica no celular
   Em Wifi, escolher Biocel_no.1
   Senha: 12345678  ;
  6. Abrir o link http://192.168.4.1

Deverá aparecer o gráfico de potencial X tempo.

De volta ao topo

Menu

1 Simulações

1.1 Equilíbrio ácido-básico e sistema tampão

Contexto:

Equação:

Sugestão:

1.2 Estado de ionização de grupos químicos de biomoléculas

Contexto:

Sugestão:

1.3 Rede de carga líquida em peptídios

Contexto:

Equação:

Sugestão:

1.4 Carga, pH, pKa & pI de aminoácidos (animação)

Contexto:

Sugestão:

1.5 Ponto Isoelétrico em Proteínas

Contexto:

Equação:

Sugestão:

1.6 Hidrofobicidade em sequências de aminoácidos

Contexto:

Equação:

Sugestão:

1.7 Interação de oxigênio com mioglobina e hemoglobina

Contexto:

Equação:

Sugestão:

1.8 Efeito de Bohr em hemoglobina (pH)

Contexto:

Equação:

Sugestão

1.9 Catálise e inibição enzimática

Contexto:

Equação:

Sugestão:

1.10 Linearização de dados cinéticos por Lineweaver-Burk

Contexto

1.10.1 Equação

Sugestão

1.11 Diagnóstico de Inibição Enzimática (Michaelis-Mentem e Lineweaver-Burk)

Contexto

Sugestão

1.12 Equação de van der Waals para gases ideais

Contexto:

Equação:

Sugestão:

1.13 Equilíbrio de produção de ATP a partir de reagentes, temperatura, e pH

Contexto:

Equação:

Sugestão:

1.14 Variação da energia de Gibbs com a temperatura

Contexto:

Equação:

Sugestão:

1.15 Consumo de Oxigênio por mitocôndria

Contexto:

Sugestão:

1.16 Espectroscopia de impedância eletroquímica (EIS)

Contexto:

Equação:

Sugestão

1.17 Voltametria cíclica

Contexto:

Equação:

Simulador de Voltametria Cíclica

Sugestão:

1.18 Diagramas e fluxogramas

Contexto: Diagrama

Sugestão:

Contexto: Fluxograma

Sugestão:

2 Construção de gráficos

2.1 Gráfico com 2 eixos de ordenadas

2.2 RangeSlider

2.3 Subplots

2.4 Subplots com tipos diferentes

2.5 Seleção múltipla sincronizada

2.6 Evento de clique & mensagem

2.7 Menu pra seleção de tipos