# Inibição por excesso de S
S <- seq(0, 10, 0.1)
v_alos <- function(S, Vm = 10, Km = 0.5, Ks = 2) {
Vm * S / (S * (1 + S / Ks) + Km)
}
curve(v_alos, xlim = c(0, 10), xlab = "S", ylab = "v")
Inibição enzimática
Tipos de inibição
Capítulo vasto na enzimologia e com aplicação direta em Química, Farmacologia, Biotecnologia, Biomedicina e áreas afins, a inibição enzimática encontra-se no âmago dos fármacos, medicamentos e biosensores. Sob um ponto de vista simplificado, a atividade enzimática pode ser reduzida na presença de vários efetores, entre moléculas endógenas ou exógenas do metabolismo celular, incluindo o próprio substrato. Genericamente a inibição enzimática classifica-se como irreversível quando a ativide decai pela ligação covalente de um inibidor, ou reversível, quando há um equilíbrio de associação/dissociação com a macromolécula. A seguir serão ilustradas inibições reversíveis.
Inibição pelo substrato
Uma inibição enzimática comum ao metabolismo é a protagonizada pelo próprio substrato em excesso no meio, sendo definida por:
\[ v=\frac{Vm*S}{S(1+\frac{S}{Ks})+Km} \tag{1}\]
Dessa forma, o gráfico resultante de uma inibição por excesso de substrato pode ser reproduzido por:
Percebe-se pela Figura 1 que a atividade da enzima alcança um limite sendo reduzida com o aumento do teor de substrato.
Modelos de inibição enzimática
Assumindo-se a relação simplificada abaixo:
\[\begin{equation}
E+S \begin{array}{c}
_{k1}\\
\rightleftharpoons\\
^{k2} \end{array} ES
\begin{array}{c}
_{k3}\\
\rightarrow \\
^{}\end{array}E+P
(\#eq:diagMM)
\end{equation}\]
A inibição de enzimas por moléculas que não o próprio substrato pode ser representada por um diagrama no qual o efetor altera um dos elementos representados na equação acima, tal como segue.
Nesse caso, pode-se definir os três tipos principais de inibição enzimática reversível como inibição competitiva, incompetitiva e não competitiva (pura ou mista). Em síntese, a inibição competitiva dá-se quando o inibidor complexa-se ao sítio ativo da enzima; a inibição incompetitiva, quando o inibidor interage com o complexo enzima-substrato; e a inibição não competitiva, quando o inibidor liga-se em outro local que não o sítio ativo da enzima, podendo ainda ser pura (Kiu = Kic) ou mista (Kiu > ou < Kic).
Um modelo matemático que abrange esses três tipos de inibição enzimática é descrito na equação abaixo:
Um modelo matemático que abrange esses três tipos de inibição enzimática é descrito na equação abaixo:
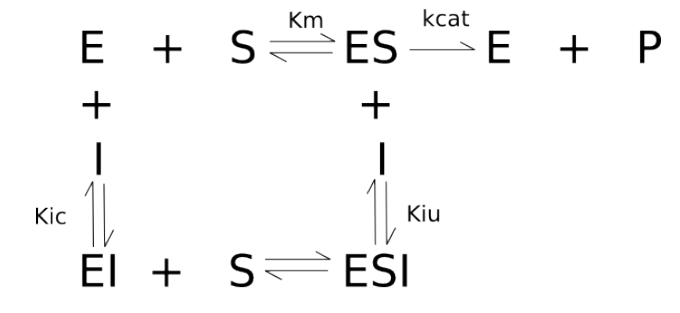
\[ v=\frac{Vm*S}{Km(1+\frac{I}{Kic})+S(1+\frac{I}{Kiu})} \tag{2}\]
Dessa forma, a Equação 2 reduz-se em seus termos multiplicadores no denominador, em função do tipo de inibição enzimática presente, até o modelo primitivo de Michaelis-Mentem, quando na ausência do inibidor.
Curva de Michaelis-Mentem para modelos de inibição enzimática
Podemos simular no
R as cuvas michaelianas para modelos clássicos de inibição, considerando valores para as constantes de equilíbrio de dissociação dos inibidores como Kic = 0.2, e Kiu = 1, como no trecho de código abaixo.# Inibição clássica & Michaelis-Mentem
par(mfrow = c(2, 2)) # divide a área de plotagem
S <- seq(0, 10, 0.1) # geração de teores de S
contr <- function(S, Vm = 10, Km = 0.5) {
Vm * S / (Km + S)
} # função de MM, sem inibição
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Competitiva")
# cuva controle; veja que o título tem que ser adicionado para o 1a. de par
# de curvas, controle e inibição
# Modelos de inibição:
# Competitiva
comp.i <- function(S, Vm = 10, Km = 0.5, I = 2, Kic = 0.2) {
Vm * S / (Km * (1 + I / Kic) + S)
}
curve(comp.i, add = TRUE, col = "red", lty = 2) # competitiva
# Não competitiva pura
pura.i <- function(S, Vm = 10, Km = 0.5, I = 2, Ki = 1) {
Vm * S / (Km * (1 + I / Ki) + S * (1 + I / Ki))
}
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Não Compet. Pura")
curve(pura.i, add = TRUE, col = "red", lty = 2) # não competitiva pura (Kiu=Kic=Ki)
# Não competitiva mista
mista.i <- function(S, Vm = 10, Km = 0.5, I = 2, Kic = 0.2, Kiu = 1) {
Vm * S / (Km * (1 + I / Kic) + S * (1 + I / Kiu))
}
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Não Compet. Mista")
curve(mista.i, add = TRUE, col = "red", lty = 2) # não competitiva mista
# Incompetitiva
incomp.i <- function(S, Vm = 10, Km = 0.5, I = 2, Kiu = 1) {
Vm * S / (Km + S * (1 + I / Kiu))
}
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Incompetitiva")
curve(incomp.i, add = TRUE, col = "red", lty = 2) # incompetitiva
layout(1) # retorna à janela gráfica original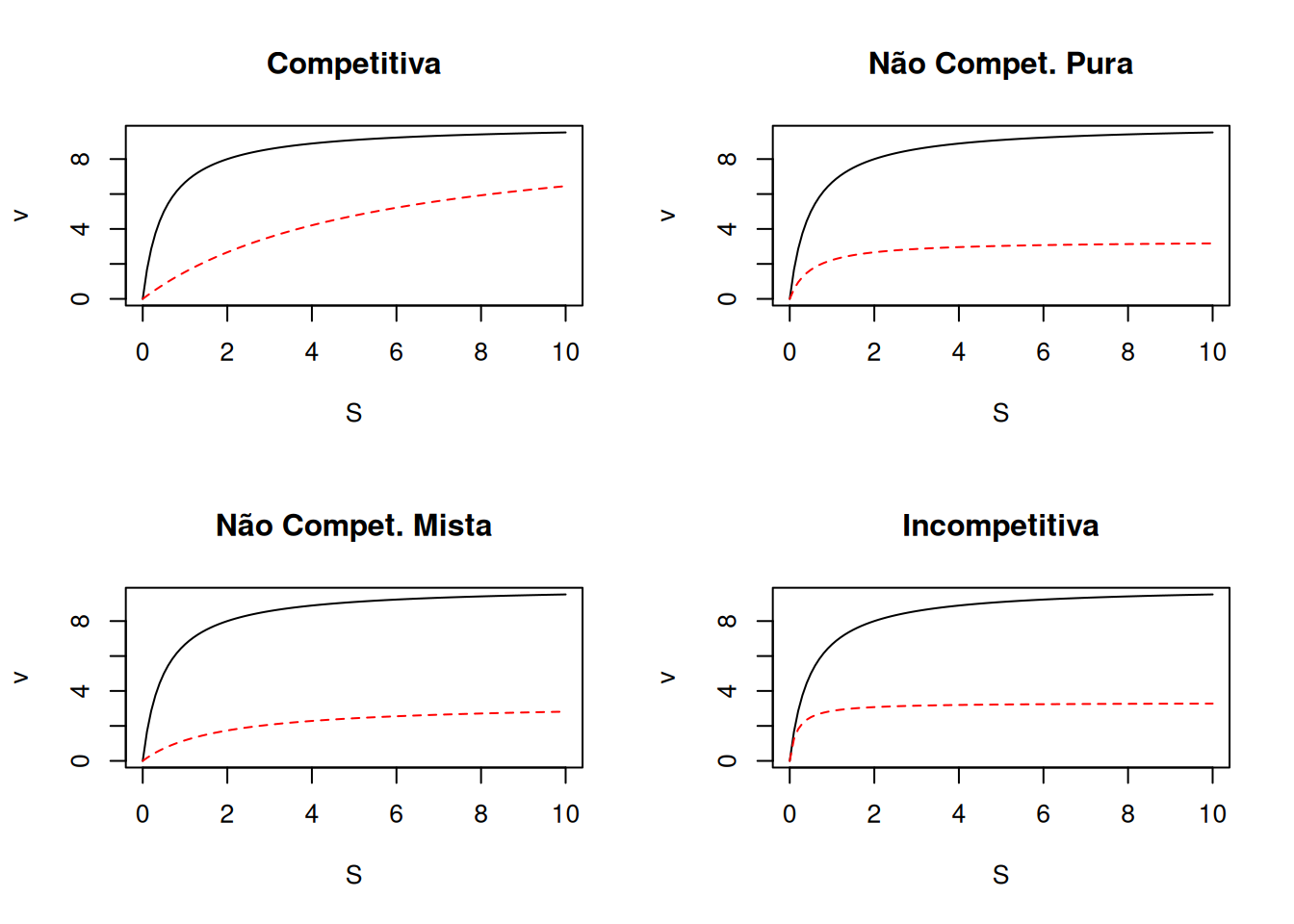
Perceba que para o modelo competitivo a velocidade limite Vm da reação tende a ser alcançada, já que a ocupação do sítio ativo da enzima é mutualmente exclusiva entre substrato e inibidor, privilegiando o primeiro quando em alto teor. Por outro lado, o valor de Vm não é tangível para os demais modelos de inibição, já que o inibidor se liga em outro sítio na enzima (não competitivo) ou ao próprio substrato (incompetitivo). Para visualizar alterações nos gráficos, experimente modificar os parâmetros da simulação (Vm, Km, Ki, Kic, Kiu, I).
Ainda que seja possível um discernimento do modelo competitivo dos demais, perceba também que isso só foi possível por uma simulação que empregou um teor S 20 vezes maior que o valor de Km da reação. Isso nem sempre é possível na prática, como elencado abaixo, já que o emprego de altos teores de S:
Ainda que seja possível um discernimento do modelo competitivo dos demais, perceba também que isso só foi possível por uma simulação que empregou um teor S 20 vezes maior que o valor de Km da reação. Isso nem sempre é possível na prática, como elencado abaixo, já que o emprego de altos teores de S:
- Agrega maior custo financeiro ao ensaio.
- Pode resultar em inibição por excesso de substrato.
- Pode elevar a viscosidade do meio, reduzindo a taxa catalítica.
Percebe-se, da Figura 2 e das observações acima, a dificuldade em classificar o tipo de inibição enzimática baseado na observação direta de uma curva de Michaelis-Mentem.
Diagnóstico de modelos de inibição enzimática por Lineweaver-Burk
As transformações lineares da equação de Michaelis-Mentem são muito úteis no diagnóstico visual de modelos de inibição. Nesse sentido, o emprego da linearização por duplos-recíprocos para esses modelos resutará nas equações de inibição que seguem:
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Kic})}{Vm}*\frac{1}{S} \quad ;\, competitivo \tag{3}\]
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Ki})}{Vm}*\frac{1}{S(1+\frac{I}{Ki})} \quad ;\, puro \tag{4}\]
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Kic})}{Vm}*\frac{1}{S(1+\frac{I}{Kiu})} \quad ;\, misto \tag{5}\]
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km}{Vm}*\frac{1}{S(1+\frac{I}{Kiu})} \quad ;\, incompetitivo \tag{6}\]
Observe que os termos multiplicadores inseridos em S e Km na equação de duplo-recíproco apenas alteram seu formalismo apresentado na equação de Lineweaver-Burk do capítulo anterior. Dessa forma, os modelos de inibição enzimática podem ser ilustrados pelo
R junto à transformação de Lineweaver-Burk (ou qualquer outra), como abaixo.# Diagnóstico de inibição por Lineweaver-Burk
# Substrato e Inibidor
S <- seq(0.1, 10, length = 10) # cria um vetor para substrato
I <- 2 # concentração de inibidor
# Parâmetros cinéticos:
Km <- 0.5
Vm <- 10
Kic <- 0.2
Ki <- 0.2
Kiu <- 1
# Equações
v <- Vm * S / (Km + S) # equação de MM
v.comp <- Vm * S / (Km * (1 + I / Kic) + S) # competitivo
v.puro <- Vm * S / (Km * (1 + I / Ki) + S * (1 + I / Ki))
# não competitivo puro
v.misto <- Vm * S / (Km * (1 + I / Kic) + S * (1 + I / Kiu))
# não competitivo misto
v.incomp <- Vm * S / (Km + S * (1 + I / Kiu))
# Gráficos
par(mfrow = c(2, 2)) # área de plot pra 4 gráficos
plot(1 / S, 1 / v, type = "l", main = "Competitivo", ylim = c(0, 2))
points(1 / S, 1 / v.comp, type = "l", col = "red")
plot(1 / S, 1 / v, type = "l", main = "Puro", ylim = c(0, 5))
points(1 / S, 1 / v.puro, type = "l", col = "red")
plot(1 / S, 1 / v, type = "l", main = "Misto", ylim = c(0, 2))
points(1 / S, 1 / v.misto, type = "l", col = "red")
plot(1 / S, 1 / v, type = "l", main = "Incompetitivo", ylim = c(0, 1))
points(1 / S, 1 / v.incomp, type = "l", col = "red")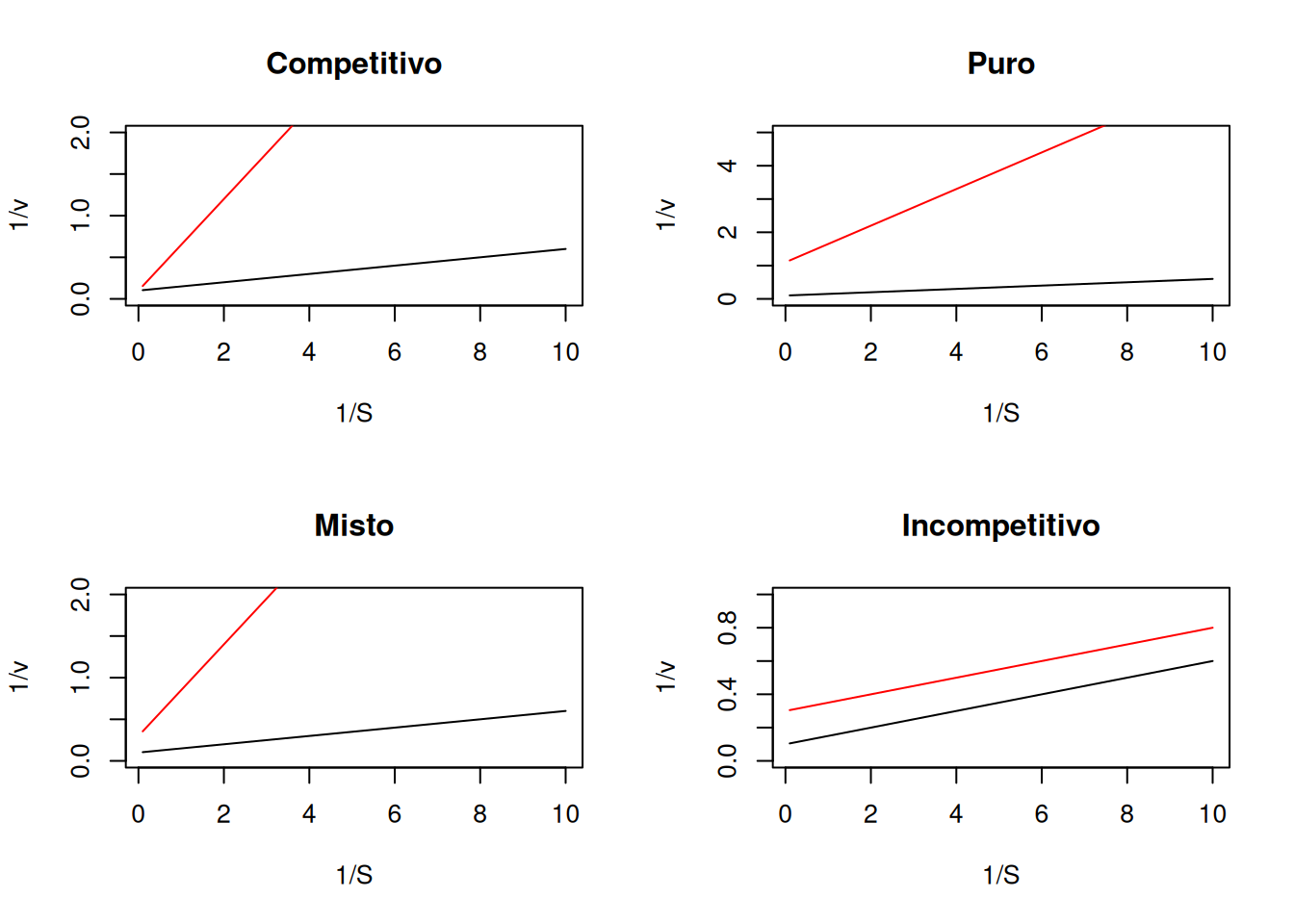
layout(1) # volta à janela gráfica normal Agora a distinção de modelos de inibição se torna mais evidente pela linearização. Assim como mencionado para os modelos representados na equação direta de Michaelis-Mentem, pode-se variar os parâmetros cinéticos e experimentar a visualização dos duplos-recíprocos.
Novamente, ainda que a linearização permita um melhor diagnóstico do tipo de inibição presente, o ajuste não linear é mais adequado para a determinação das constantes de inibição (Ki’s), uma vez que não agrega os erros advindos das transformações lineares (embora a inserção de pesos estatísticos possa aliviar a imprecisão dos resultados).
Novamente, ainda que a linearização permita um melhor diagnóstico do tipo de inibição presente, o ajuste não linear é mais adequado para a determinação das constantes de inibição (Ki’s), uma vez que não agrega os erros advindos das transformações lineares (embora a inserção de pesos estatísticos possa aliviar a imprecisão dos resultados).
Ki & IC\(_{50}\)
A concentração inibitória a 50% do teor de inibidor, definida como IC\(_{50}\), pode ser determinada empiricamente sem o conhecimento dos parâmetros de catálise enzimática envolvidos. Para isso, basta se obter um valor de inibição relativa num ensaio a concentração fixa de S, variando-se o teor de inibidor. De fato, análogos ao IC\(_{50}\) existem em ampla gama nas Ciências Naturais, não envolvendo necessariamente qualquer informação cinética ou termodinâmica dos compostos envolvidos, mas tão somente a informação empírica do resultado. Exemplificando, os parâmetros DE\(_{50}\) (dose efetiva) ou DL\(_{50}\) (dose letal), e mesmo projeções de X\(_{50}\), tal como Tm (temperatura de desnaturação a 50%), e o valor de pKa em tampões (pH em que as espécies encontram-se 50% ionizadas/protonadas em solução).
No entanto, existe uma relação útil entre a constante de equilíbrio de dissociação do inibidor Ki e o valor de IC\(_{50}\) que permite sua permuta, desde que conhecido o modelo de inibição [@yung1973relationship]. Generalizando para os modelos de inibição, pode-se definir uma equação geral pra relação de Cheng-Prusoff como:
No entanto, existe uma relação útil entre a constante de equilíbrio de dissociação do inibidor Ki e o valor de IC\(_{50}\) que permite sua permuta, desde que conhecido o modelo de inibição [@yung1973relationship]. Generalizando para os modelos de inibição, pode-se definir uma equação geral pra relação de Cheng-Prusoff como:
\[ IC_{50} = \frac{(1+\frac{S}{Km})}{(\frac{1}{Kic})+(\frac{1}{Km*Kiu})} \tag{7}\]
Exemplificando, para um modelo competitivo de inibição, onde Kiu é nulo:
\[ IC_{50} = Kic(1+\frac{S}{Km}) \tag{8}\]
Como acima mencionado, o valor de IC\(_{50}\) pode ser obtido a partir de dados experimentais de inibição relativa (v/Vm, por ex) em diferentes concentrações de inibidor fixando um valor de S. Nesse caso, podemos ilustrar no
R a obtenção de IC\(_{50}\), utilizando-se um ajuste não linear para a equação de quatro parâmetros que segue (curva de Rodbard, @delean1978simultaneous).\[ ativ. residual \, \% =\frac{v}{Vm} = inf+\frac{sup-inf}{1+log(\frac{I}{IC_{50}})^{nH}}) \] {#eq:eqRodb}
# Ajuste não-linear para curva de IC50
logI.nM <- c(5.5, 5.2, 4.9, 4.6, 4.3, 3.7, 3.3, 3, 2.8)
# conc. de I, em unidade log10
ativ.res <- c(0.02, 0.07, 0.12, 0.22, 0.36, 0.53, 0.67, 0.83, 0.85)
# ativ. residual, v/Vm
dados <- data.frame(logI.nM, ativ.res) # criação do dataframe
plot(ativ.res ~ logI.nM, dados) # plot dos dados
ic50.fit <- nls(formula(ativ.res ~ inf + (sup - inf) /
(1 + (logI.nM / logIC50)^nH)),
algorithm = "port", data = dados,
start = list(inf = 0, sup = 0.80, logIC50 = 4, nH = 10),
lower = c(inf = -Inf, sup = -Inf,
logIC50 = 0, nH = -Inf)) # ajuste não linear
summary(ic50.fit) # sumário do ajuste
Formula: ativ.res ~ inf + (sup - inf)/(1 + (logI.nM/logIC50)^nH)
Parameters:
Estimate Std. Error t value Pr(>|t|)
inf -0.3211 0.2932 -1.095 0.32348
sup 1.1200 0.2311 4.847 0.00469 **
logIC50 4.0807 0.2309 17.675 1.06e-05 ***
nH 4.0540 1.7462 2.322 0.06792 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.02769 on 5 degrees of freedom
Algorithm "port", convergence message: relative convergence (4)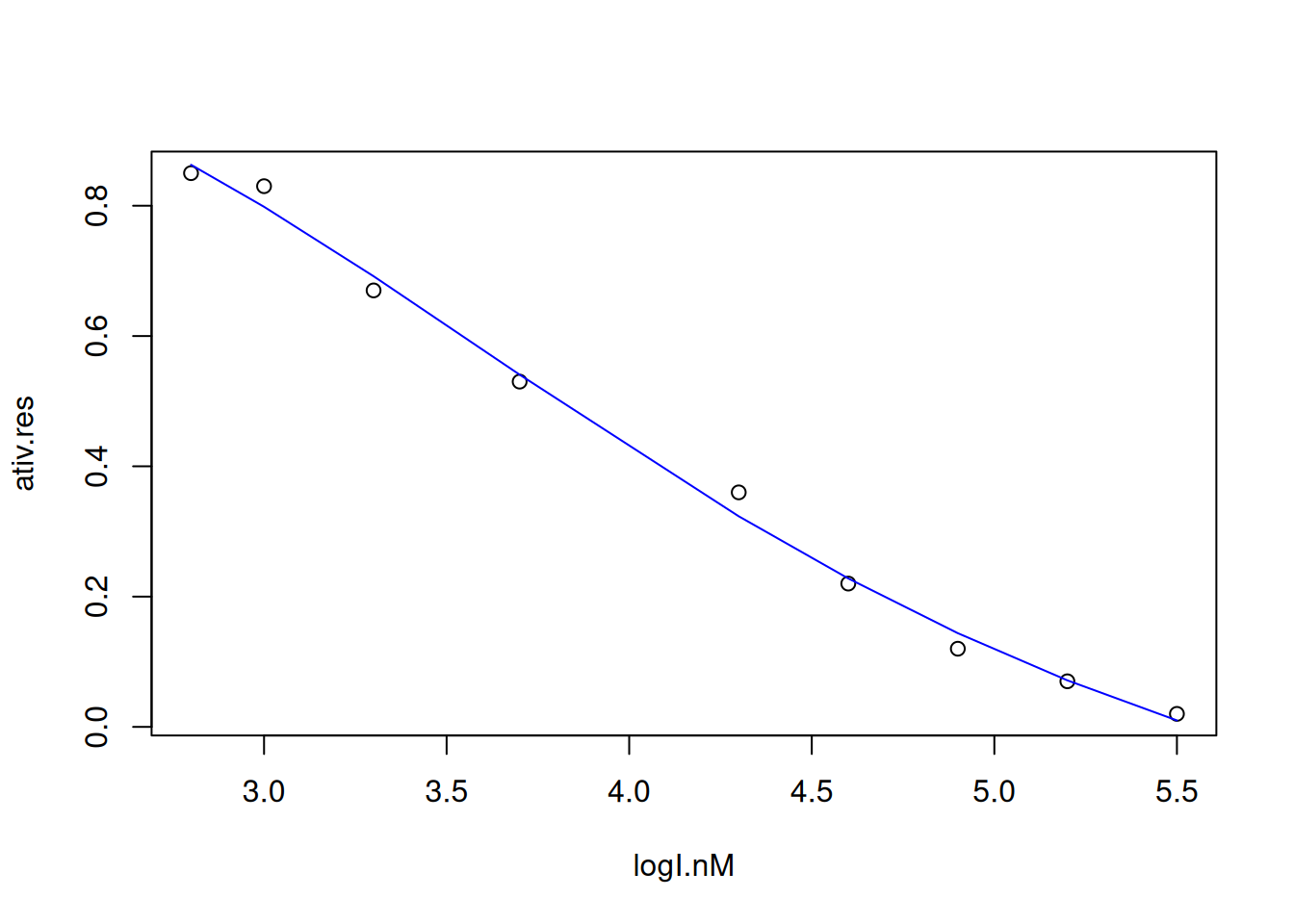lines(logI.nM, fitted(ic50.fit), col = "blue") # linha ajustada
# E para extrair o valor de IC50...
IC50 <- 10^(coef(ic50.fit)[3]) # extração do 3o. parâmetro da tabela
# de ajuste, isto é: logIC50:
IC50 logIC50
12042.04 Perceba que o parâmetro de logIC50 foi extraído da tabela de ajuste não linear pelo comando
Para isso, podemos utilizar duas funções do
coef. Isto é muito útil quando desejamos utilizar um coeficiente obtido em cálculos automáticos (programáveis), como veremos mais adiante. Por ora, faz-se interessante apresentar o parâmetro de IC50 obtido de forma mais elegante.Para isso, podemos utilizar duas funções do
R para exprimir resultados quantitativos junto à caracteres (palavras, frases): print() e cat. O trecho de código abaixo ilustra esse output, e algumas diferenças.cat("Valor de IC50 (nM):", IC50, "\n")Valor de IC50 (nM): 12042.04 print(paste("Valor de IC50 (nM):", IC50))[1] "Valor de IC50 (nM): 12042.0403466162" Basicamente,
print exibe aspas e indexa o nome da coluna, enquanto cat os omite. Em adição, pode-se perceber outra variação no formato de impressão entre os dois comandos pelo exemplo abaixo:print(paste("teores:", c(10, 25, 50)))[1] "teores: 10" "teores: 25" "teores: 50"cat("teores:", c(10, 25, 50))teores: 10 25 50 Outra possibilidade no
R é a de se reduzir o número de casas decimais apresentados. Nesse caso, pode-se utilizar o comando round.IC50 <- 10^(coef(ic50.fit)[3])
print(paste("Valor de IC50 (nM):", round(IC50, digits = 2))) [1] "Valor de IC50 (nM): 12042.04"# arredondamento para duas casas decimais Mais uma vez, salienta-se a existência de alguns pacotes úteis do
R para o cálculo de IC50, entre esse o pacote drc (dose-response curve).Diagnóstico estatístico de inibição enzimática
Em paralelo à inspeção visual dos gráficos de linearização para inibição enzimática, é possível validar-se um modelo sobre outro por uma análise de dispersão de erros dos modelos. Mas também é possível o emprego da função
Matematicamente, BIC e AIC podem ser expressos como:
BIC ou da função AIC do R, e que respectivamente calculam valores para o Critério de Informação Bayseiano [@spiess2010evaluation] ou do Critério de Informação de Akaike [@akaike1974new]. Em comum esse parâmetros calculam um valor relativo de informação não computada por um modelo avaliado. O menor valor encontrado para ambos espelha a solução do melhor modelo de ajuste.Matematicamente, BIC e AIC podem ser expressos como:
\[ BIC = p*ln(n)-2*ln(RSE)\\ \\ AIC = n*ln(\frac{RSE}{n})+2k+[\frac{2k(k+1)}{n-k-1}])\\ \tag{9}\]
Onde p representa o no. de parâmetros do modelo, n o número total de pontos experimentais, k o fator p+1, e RSE o valor da soma dos quadrados dos resíduos (residual sum squares).
Para exemplificar o uso desses parâmetros de qualidade do modelo estatístico, pode-se empregar um conjunto de dados contido no pacote
nlstools, provendo o ajuste, plotagem, inspeção de resíduos, e aplicação de BIC e AIC:# Aplicação de critérios de informação para ajuste de curvas cinéticas
library(nlstools)
comp <- nls(compet_mich, vmkmki, list(Km = 1, Vmax = 20, Ki = 0.5))
# ajuste competitivo, com dados, equação e sementes fornecidas
# pelo pacote nlstools
plotfit(comp, variable = 1) # comando de plotagem do pacote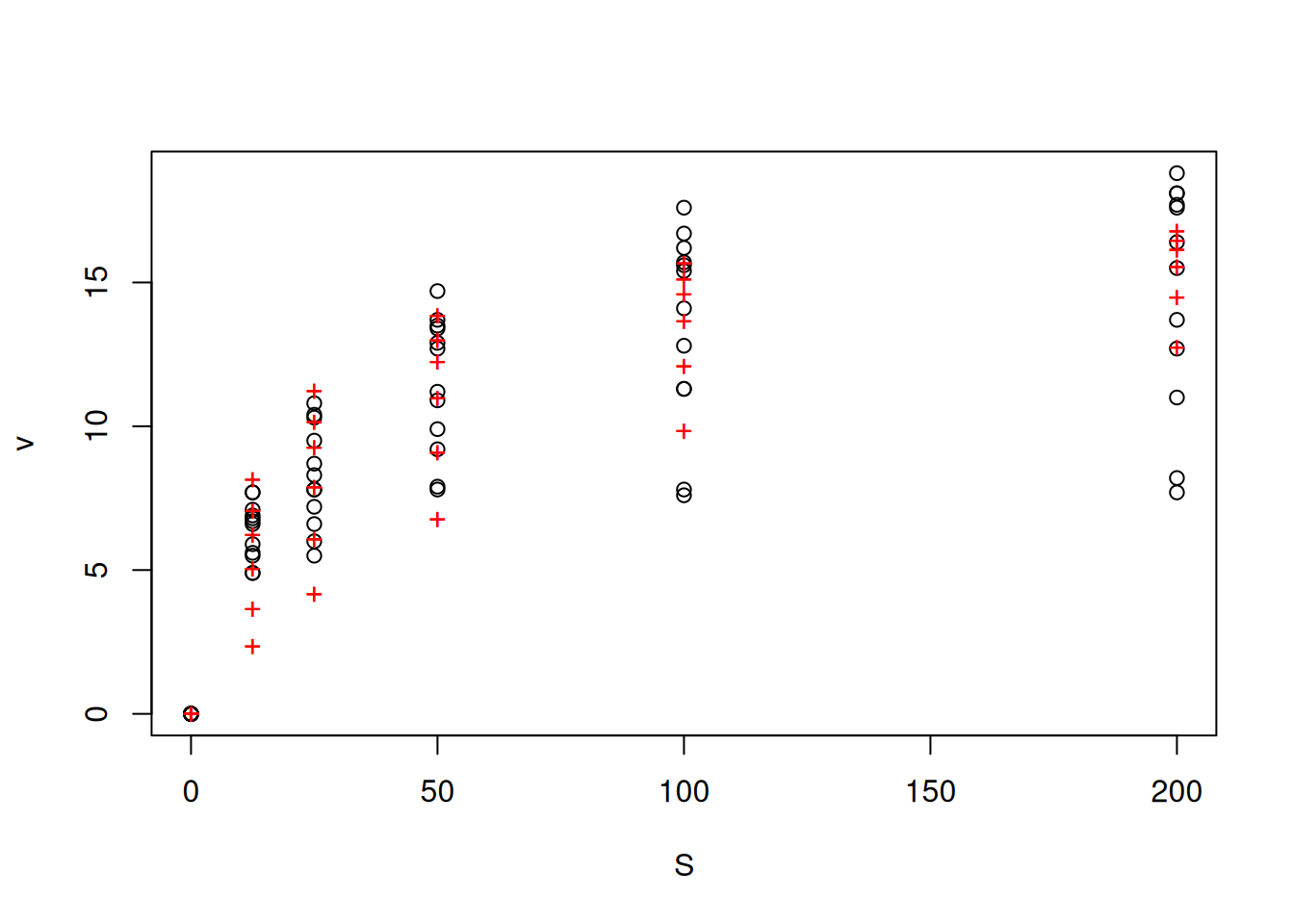
summary(comp)
Formula: v ~ S/(S + Km * (1 + I/Ki)) * Vmax
Parameters:
Estimate Std. Error t value Pr(>|t|)
Km 15.2145 2.5005 6.085 5.79e-08 ***
Vmax 18.0557 0.6288 28.713 < 2e-16 ***
Ki 22.2822 4.9060 4.542 2.30e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.603 on 69 degrees of freedom
Number of iterations to convergence: 11
Achieved convergence tolerance: 5.116e-06res_comp <- nlsResiduals(comp) # resíduos do ajuste
plot(res_comp, which = 1) # plotagem de resíduos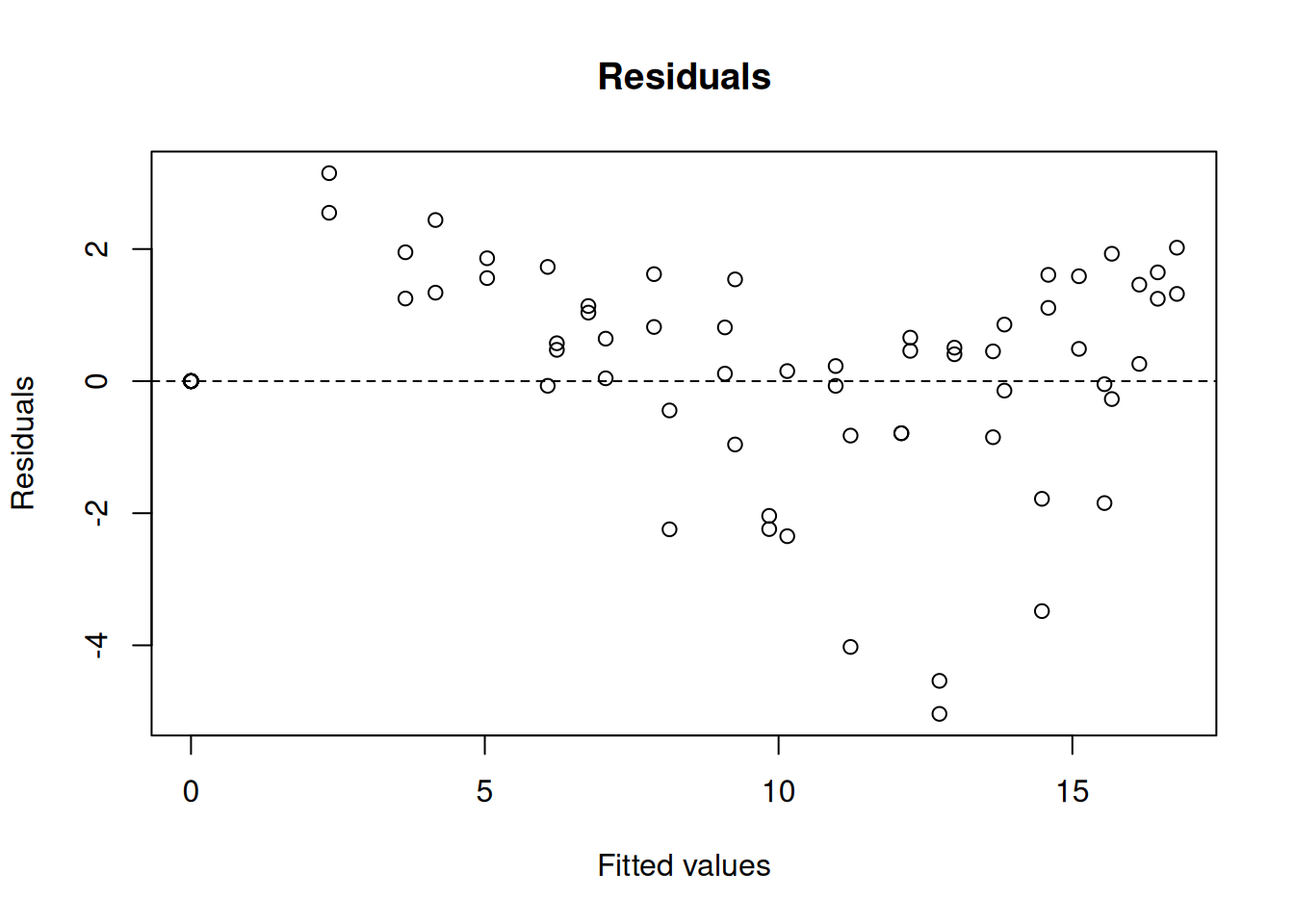
noncomp <- nls(non_compet_mich, vmkmki, list(Km = 1, Vmax = 20, Ki = 0.5))
# o mesmo que acima, mas para o modelo não competitivo
plotfit(noncomp, variable = 1)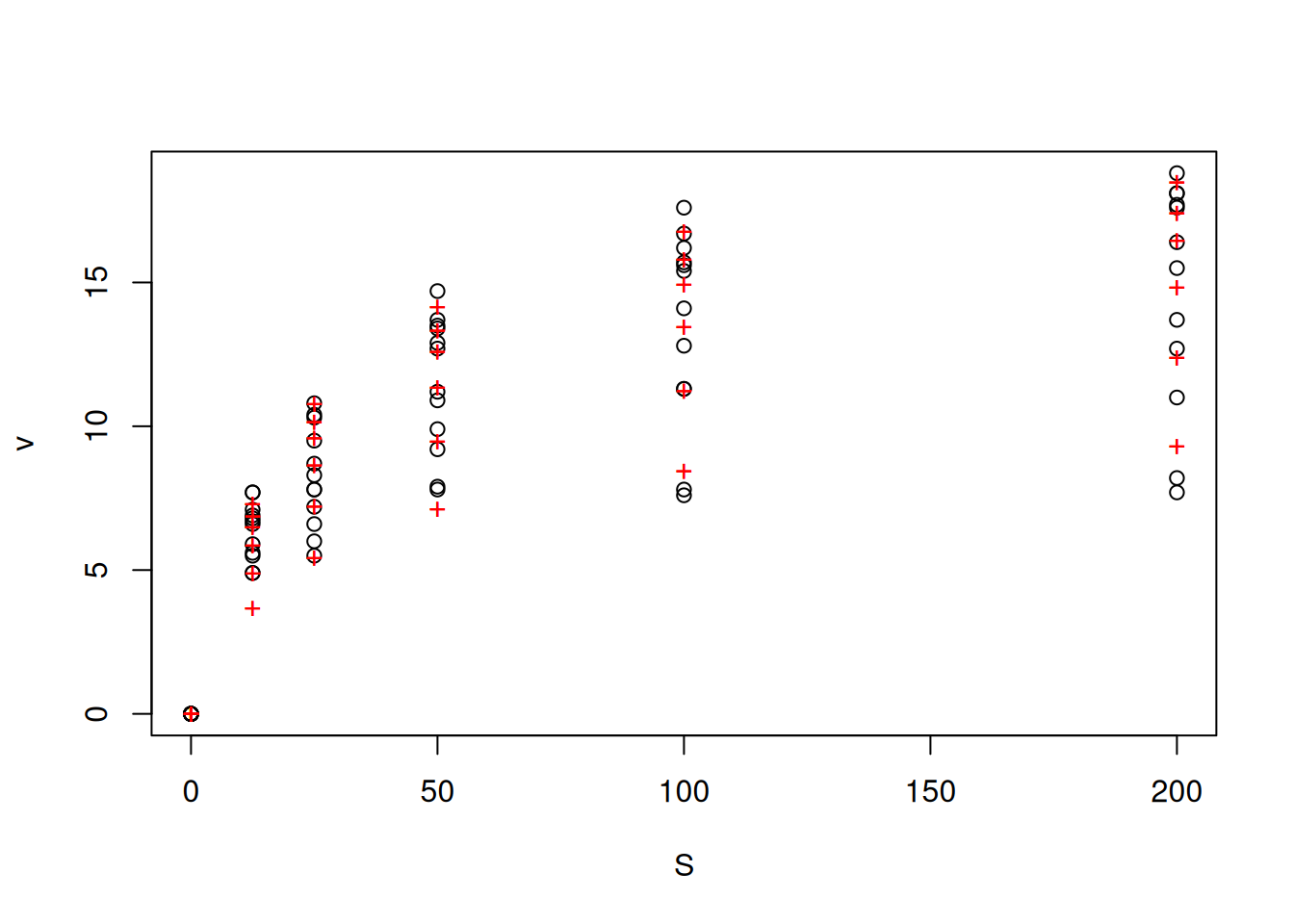
summary(noncomp)
Formula: v ~ S/((S + Km) * (1 + I/Ki)) * Vmax
Parameters:
Estimate Std. Error t value Pr(>|t|)
Km 22.7787 1.4738 15.46 <2e-16 ***
Vmax 20.5867 0.4306 47.80 <2e-16 ***
Ki 101.3563 7.3303 13.83 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8925 on 69 degrees of freedom
Number of iterations to convergence: 7
Achieved convergence tolerance: 8.27e-06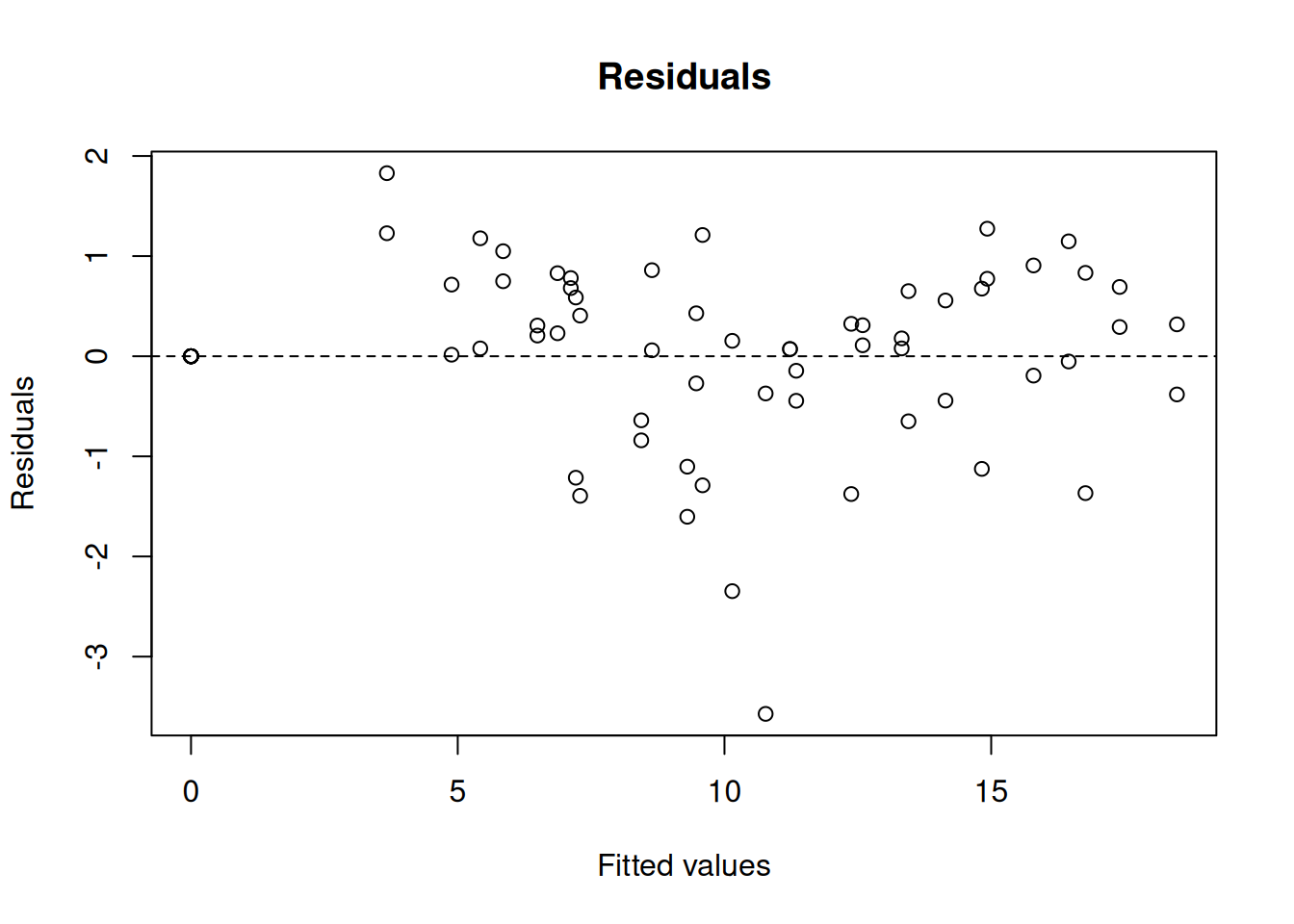res_noncomp <- nlsResiduals(noncomp)
plot(res_noncomp, which = 1)
BIC(comp, noncomp) # Critério de informação de Baysean df BIC
comp 4 286.2994
noncomp 4 201.9981AIC(comp, noncomp) # Critério de informação de Akaike df AIC
comp 4 277.1928
noncomp 4 192.8915 Pode-se observar na comparação dos ajustes não lineares que o modelo não competitivo ajustou-se melhor que o modelo competitivo (valores menores para BIC e AIC)
Cinética de estado pré-estacionário
Existem basicamente três tipos de comportamentos cinéticos para as enzimas: comportamento de Henry-Michaelis-Mentem-Briggs-Haldane, sucintamente denominado por michaeliano ou de estado estacionário (steady-state), comportamento de fase lag (quando o substrato leva algum tempo para ser convertido em produto), e comportamento de burst, transiente, ou de estado pré-estacionário (quando uma fase com rápida liberação de produto precede o estado estacionário). Algumas enzimas trabalham seguindo a cinética de burst, entre as quais algumas nucleosidades e glicosidases, e dehalogenases [@johnson19921,@tang2003kinetic].
A cinética de estado pré-estacionário segue um formalismo um pouco distinto, e que depende do quantitativo de etapas reacionais. Exemplificando abaixo para uma reação de 3 etapas [@johnson19921]:
A cinética de estado pré-estacionário segue um formalismo um pouco distinto, e que depende do quantitativo de etapas reacionais. Exemplificando abaixo para uma reação de 3 etapas [@johnson19921]:
\[ E+S \begin{array}{c} _{k1}\\ \rightleftharpoons\\ ^{km1} \end{array} E*S \begin{array}{c} _{k2}\\ \rightleftharpoons\\ ^{km2} \end{array} E*P \begin{array}{c} _{k3}\\ \rightarrow \\ ^{}\end{array} E+P \tag{10}\]
Nesse caso, as equações derivadas das observações experimentais, e que conduzem à determinação das constantes de velocidade são:
\[ kobs=k2+km2+k3 \tag{11}\]
\[ Ao=\frac{k2*(k2+km2)}{kobs^2} \tag{12}\]
\[ kcat=\frac{k2*k3}{kobs} \tag{13}\]
Onde kobs e Ao representam parâmetros experimentais de constante de velocidade observada e amplitude, respectivamente. Esses parâmetros podem ser obtidos a partir do ajuste não linear da equação abaixo aos dados experimentais:
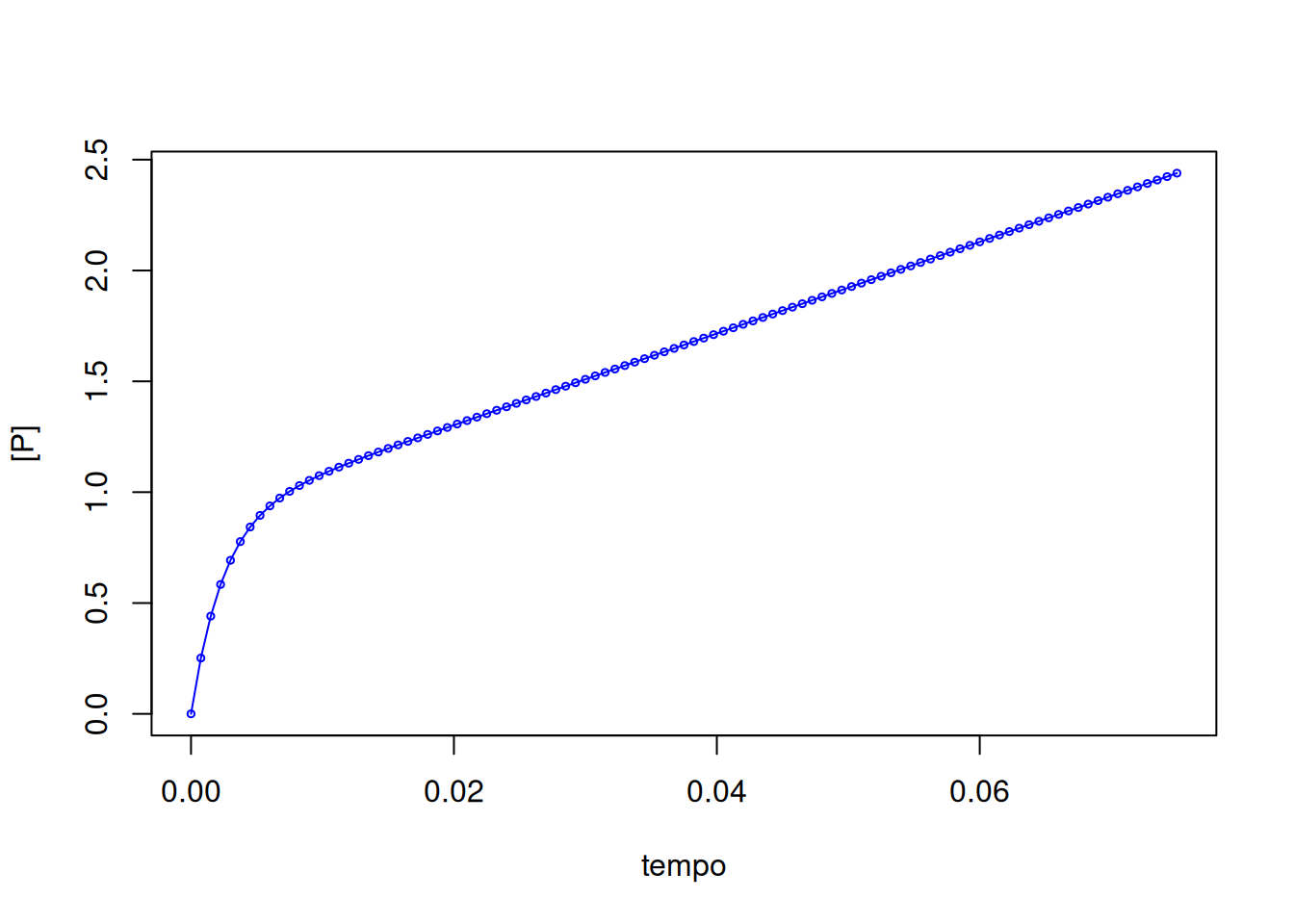
\[ P=Ao(1-e^ {-kobs} + kcat * t) \tag{14}\]
O trecho de código que segue simula uma curva de comportamento pré-estacionário, quando conhecidas as constantes de velocidade que determinam os parâmetros experimentais.
# Curva de MM em enzima de comportamento pré-estacionário
# Parâmetros
k2 <- 387
km2 <- 3
k3 <- 22
xmin <- 0
xmax <- 0.075 # definição de limites para função
# Variáveis da equação de simulação (função dos parâmetros)
kobs <- k2 + km2 + k3
Ao <- k2 * (k2 + km2) / kobs^2
kcat <- k2 * k3 / kobs
# Definição da função de simulação
sim <- function(x, kobs, Ao, kcat) {
Ao * (1 - exp(-kobs * x)) + kcat * x
}
# Curval de simulação
curve(sim(x, kobs = kobs, Ao = Ao, kcat = kcat),
col = "blue",
type = "o", xlim = c(xmin, xmax), cex = 0.5,
xlab = "tempo", ylab = "[P]"
)
Note pela Figura 3 que na cinética de estado transiente, existe uma fase pré-estacionária inicial eleva o teor de produto P rapidamente, e que antecede a fase estacionária de liberação constante de P.
Por outro lado, por vezes é necessário o oposto, ou seja, determinar as constantes de velocidade a partir do conhecimento dos parâmetros experimentais kobs e Ao. Nesse caso (e em tantos outros transdisciplinares) o
O procedimento envolve minimizar iterativamente um vetor de equações dadas as sementes para cada parâmetro. Para tal busca-se obter f(x) = 0 pela diferença entre um valor de referência; ou seja, quando a solução encontrar x quando f(x)-y = 0. Exemplificando, supondo que f(x) seja a+b/x, e que y seja 3. Então a busca se dá no sentido de encontrar a e b em a+b/x-3.
Para a determinação das constantes de velocidade representadas na cinética transiente, vale mencionar a função
Na solução dos parâmetros para estado pré-estacionário, ilustra-se abaixo o emprego do
R possui funções de minimização que permitem encontrar a raíz de equações lineares ou não lineares.O procedimento envolve minimizar iterativamente um vetor de equações dadas as sementes para cada parâmetro. Para tal busca-se obter f(x) = 0 pela diferença entre um valor de referência; ou seja, quando a solução encontrar x quando f(x)-y = 0. Exemplificando, supondo que f(x) seja a+b/x, e que y seja 3. Então a busca se dá no sentido de encontrar a e b em a+b/x-3.
Para a determinação das constantes de velocidade representadas na cinética transiente, vale mencionar a função
optim em stats ou o pacote rootSolve, que buscam minimizar equações lineares e não lineares para encontrar os valores de seus parâmetros.Na solução dos parâmetros para estado pré-estacionário, ilustra-se abaixo o emprego do
R com rootSolve, adicionando ainda a busca para Km como segue.\[ Km = \frac{k3}{k2+k3} \] {#eq:burstKm}
# Cálculo de constantes cinéticas por solução de sistema de equações
# não lineares aplicadas à cinética de burst.
library(rootSolve)
kobs <- 0.06
Ao <- 50
kcat <- 300
Ks <- 15
# define os parâmetros de ajuste não linear obtidos por curva progressiva
# experimental, t x P;
# Obs: Ks obtido experimentalmente de curva de S x kobs
# Parâmetros
# x[1]=k2
# x[2]= k3
# x[3] = Km
# Modelo
model <- function(x) c(x[1] / kobs^2 - Ao, (x[1] * x[2]) / kobs - kcat,
Ks * x[2] / (x[1] + x[2]) - x[3])
# o modelo acima deve conter uma lista de equações cuja igualdade é zero,
# ou seja, f(x)=0
(ss <- multiroot(model, c(1, 1, 1))) # comando de execução do rootSolve$root
[1] 0.18000 100.00000 14.97305
$f.root
[1] 0.000000e+00 1.136868e-13 -1.243054e-09
$iter
[1] 4
$estim.precis
[1] 4.143891e-10# (sementes pro algoritmo) Os resultados da minimização podem ser interpretados como:
- root = valores de xi pra f(xi)=0 ; ou seja, k2, k3, e Km;
- f.root = valor de cada função pra cada xi (deve ser próximo de zero para cada);
- iter = no. iterações ;
- esti.precis = estimativa da precisão.
A contemplar um capítulo ainda que extenso sobre cinética enzimática, existem inúmeros tópicos deixados de lado, dado o foco principal do emprego do
R na solução de problemas quantitativos em biofísico-química. Dessa forma, omitimos diversos conceitos, tais como cinética lenta de interação de substrato (slow binding), cinética de múltiplos substratos (reação sequencial e ping-pong), equação integrada de Michaelis-Menten e curvas progressivas, ativação de moduladores, influência de pH e temperatura na catálise, e enzimas multisítios, entre vários.