# Inhibition due to excess S
S <- seq(0, 10, 0.1)
v_alos <- function(S, Vm = 10, Km = 0.5, Ks = 2) {
Vm * S / (S * (1 + S / Ks) + Km)
}
curve(v_alos, xlim = c(0, 10), xlab = "S", ylab = "v")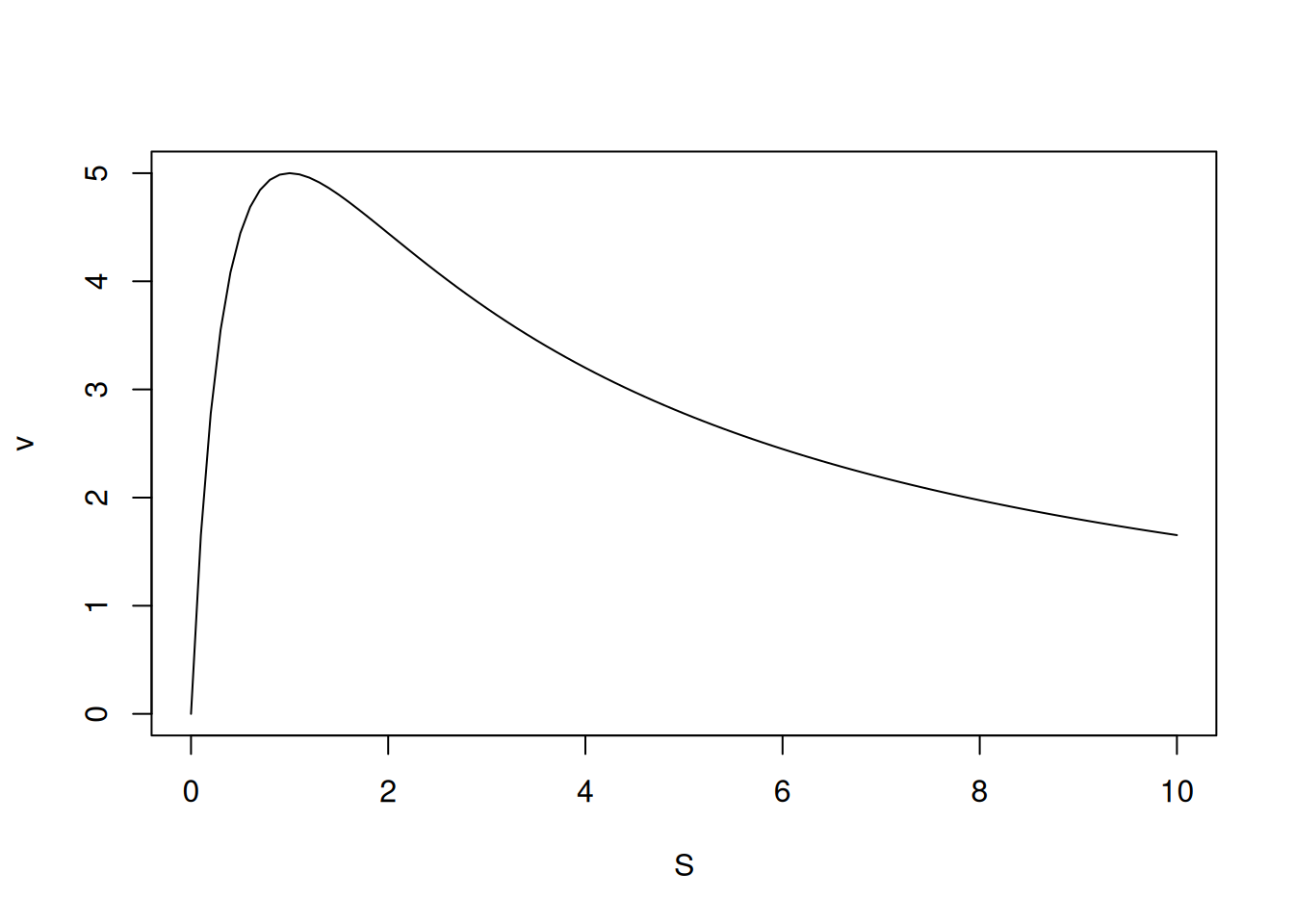
Enzyme inhibition
Types of inhibition
A vast chapter in enzymology and with direct application in Chemistry, Pharmacology, Biotechnology, Biomedicine and related areas, enzyme inhibition is at the heart of drugs, medicines and biosensors. From a simplified point of view, enzyme activity can be reduced in the presence of several effectors, among endogenous or exogenous molecules of cellular metabolism, including the substrate itself. Generically, enzyme inhibition is classified as irreversible when the activity decreases due to the covalent binding of an inhibitor, or reversible, when there is an equilibrium of association/dissociation with the macromolecule. Reversible inhibitions will be illustrated below.
Inhibition by the substrate
A common enzyme inhibition in metabolism is caused by the substrate itself in excess in the medium, defined by:
\[ v=\frac{Vm*S}{S(1+\frac{S}{Ks})+Km} \tag{1}\]
Thus, the graph resulting from an inhibition due to excess substrate can be reproduced by:
It can be seen from Figure 1 that the enzyme activity reaches a limit and is reduced with increasing substrate content.
Enzyme inhibition models
Assuming the simplified relation below:
\[\begin{equation}
E+S \begin{array}{c}
_{k1}\\
\rightleftharpoons\\
^{k2} \end{array} ES
\begin{array}{c}
_{k3}\\
\rightarrow \\
^{}\end{array}E+P
(\#eq:diagMM)
\end{equation}\]
Enzyme inhibition by molecules other than the substrate itself can be represented by a diagram in which the effector alters one of the elements represented in the above equation, as follows.
In this case, the three main types of reversible enzyme inhibition can be defined as competitive, uncompetitive and non-competitive (pure or mixed) inhibition. In summary, competitive inhibition occurs when the inhibitor complexes with the enzyme’s active site; uncompetitive inhibition, when the inhibitor interacts with the enzyme-substrate complex; and non-competitive inhibition, when the inhibitor binds to a site other than the enzyme’s active site, and can also be pure (Kiu = Kic) or mixed (Kiu > or < Kic).
A mathematical model that encompasses these three types of enzyme inhibition is described in the equation below:
A mathematical model that encompasses these three types of enzyme inhibition is described in the equation below:
\[ v=\frac{Vm*S}{Km(1+\frac{I}{Kic})+S(1+\frac{I}{Kiu})} \tag{2}\]
Thus, Equation 2 is reduced in its multiplying terms in the denominator, depending on the type of enzyme inhibition present, up to the primitive Michaelis-Mentem model, when there is no inhibitor.
Michaelis-Mentem curve for enzyme inhibition models
We can simulate in
R the Michaelian curves for classical inhibition models, considering values for the inhibitor dissociation equilibrium constants such as Kic = 0.2, and Kiu = 1, as in the code snippet below.# Classical inhibition & Michaelis-Mentem
par(mfrow = c(2, 2)) # divide the plot area
S <- seq(0, 10, 0.1) # generation of S contents
contr <- function(S, Vm = 10, Km = 0.5) {
Vm * S / (Km + S)
} # MM function, without inhibition
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Competitive")
# control curve; note that the title has to be added for the 1a. of pair
# of curves, control and inhibition
# Inhibition models:
# Competitive
comp.i <- function(S, Vm = 10, Km = 0.5, I = 2, Kic = 0.2) {
Vm * S / (Km * (1 + I / Kic) + S)
}
curve(comp.i, add = TRUE, col = "red", lty = 2) # competitive
# Pure noncompetitive
pura.i <- function(S, Vm = 10, Km = 0.5, I = 2, Ki = 1) {
Vm * S / (Km * (1 + I / Ki) + S * (1 + I / Ki))
}
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Pure Noncompet.")
curve(pura.i, add = TRUE, col = "red", lty = 2) # pure non-competitive (Kiu=Kic=Ki)
# Mixed non-competitive
mista.i <- function(S, Vm = 10, Km = 0.5, I = 2, Kic = 0.2, Kiu = 1) {
Vm * S / (Km * (1 + I / Kic) + S * (1 + I / Kiu))
}
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Non-Compet. Mixed")
curve(mista.i, add = TRUE, col = "red", lty = 2) # mixed non-competitive
# Uncompetitive
uncomp.i <- function(S, Vm = 10, Km = 0.5, I = 2, Kiu = 1) {
Vm * S / (Km + S * (1 + I / Kiu))
}
curve(contr, xlim = c(0, 10), xlab = "S", ylab = "v", main = "Uncompetitive")
curve(uncomp.i, add = TRUE, col = "red", lty = 2) # uncompetitive
layout(1) # returns to the original graphic window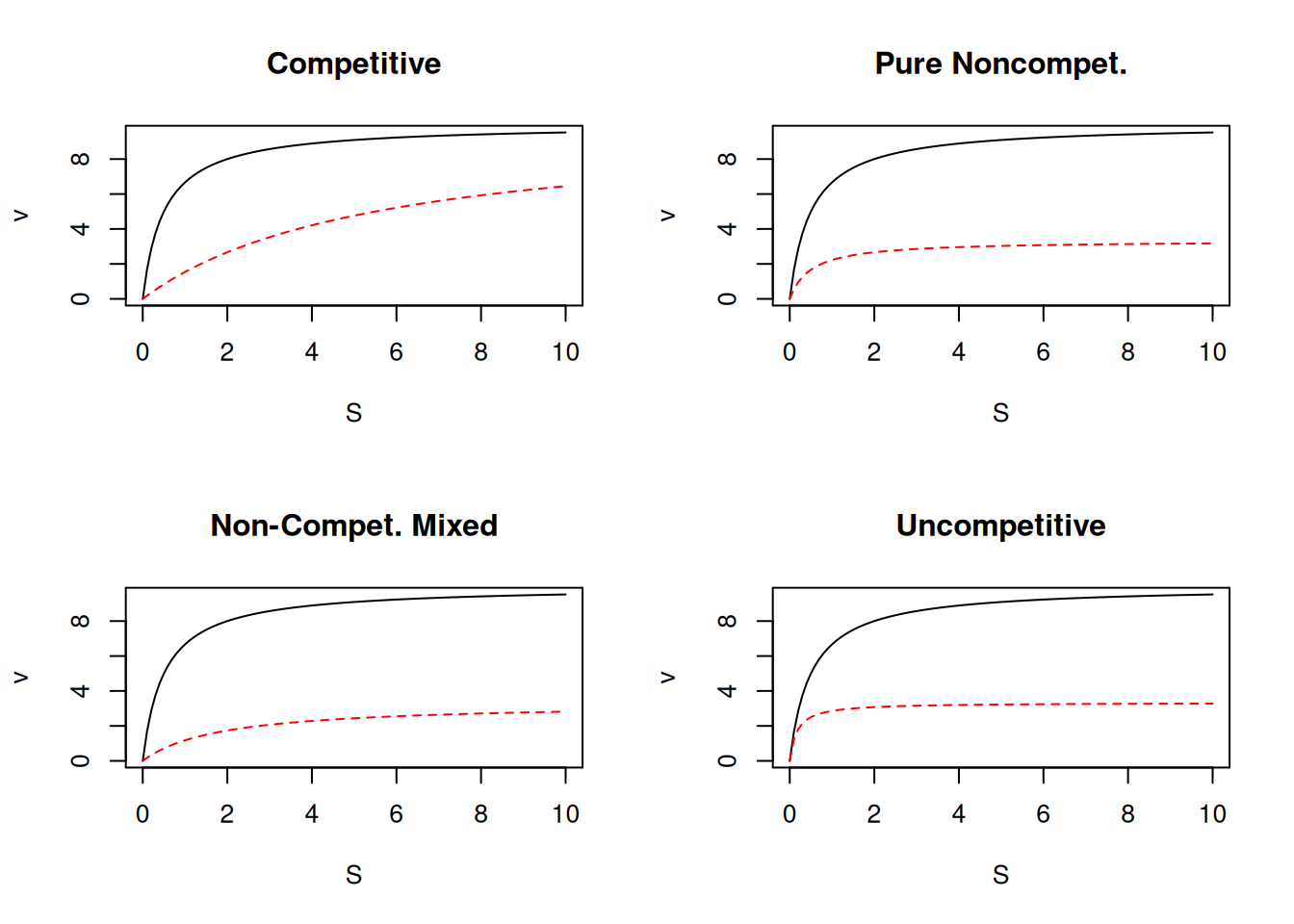
Note that for the competitive model the limiting reaction rate Vm tends to be reached, since the occupation of the enzyme’s active site is mutually exclusive between substrate and inhibitor, favoring the former when in high concentration. On the other hand, the Vm value is not tangible for the other inhibition models, since the inhibitor binds to another site on the enzyme (non-competitive) or to the substrate itself (uncompetitive). To see changes in the graphs, try modifying the simulation parameters (Vm, Km, Ki, Kic, Kiu, I).
Although it is possible to distinguish the competitive model from the others, also note that this was only possible for a simulation that used an S content 20 times greater than the Km value of the reaction. This is not always possible in practice, as listed below, since the use of high S contents:
Although it is possible to distinguish the competitive model from the others, also note that this was only possible for a simulation that used an S content 20 times greater than the Km value of the reaction. This is not always possible in practice, as listed below, since the use of high S contents:
- Adds greater financial cost to the test.
- May result in inhibition due to excess substrate.
- May increase the viscosity of the medium, reducing the catalytic rate.
It can be seen from Figure 2 and the observations above that it is difficult to classify the type of enzyme inhibition based on direct observation of a Michaelis-Mentem curve.
Diagnosis of enzyme inhibition models by Lineweaver-Burk
Linear transformations of the Michaelis-Mentem equation are very useful in the visual diagnosis of inhibition models. In this sense, the use of double-reciprocal linearization for these models will result in the following inhibition equations:
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Kic})}{Vm}*\frac{1}{S} \quad ;\, competitive \tag{3}\]
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Ki})}{Vm}*\frac{1}{S(1+\frac{I}{Ki})} \quad ;\, pure \tag{4}\]
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km(1+\frac{I}{Kic})}{Vm}*\frac{1}{S(1+\frac{I}{Kiu})} \quad ;\, mixed \tag{5}\]
\[ \frac{1}{v}=\frac{1}{Vm}+\frac{Km}{Vm}*\frac{1}{S(1+\frac{I}{Kiu})} \quad ;\, uncompetitive \tag{6}\]
Note that the multiplier terms inserted in S and Km in the double-reciprocal equation only change its formalism presented in the Lineweaver-Burk equation of the previous chapter. Thus, enzyme inhibition models can be illustrated by
R together with the Lineweaver-Burk transformation (or any other), as below.# Diagnosis of inhibition by Lineweaver-Burk
# Substrate and Inhibitor
S <- seq(0.1, 10, length = 10) # create a vector for substrate
I <- 2 # inhibitor concentration
# Kinetic parameters:
Km <- 0.5
Vm <- 10
Kic <- 0.2
Ki <- 0.2
Kiu <- 1
# Equations
v <- Vm * S / (Km + S) # MM equation
v.comp <- Vm * S / (Km * (1 + I / Kic) + S) # competitive
v.pure <- Vm * S / (Km * (1 + I / Ki) + S * (1 + I / Ki))
# pure non-competitive
v.mixed <- Vm * S / (Km * (1 + I / Kic) + S * (1 + I / Kiu))
# mixed non-competitive
v.incomp <- Vm * S / (Km + S * (1 + I / Kiu))
# Graphics
par(mfrow = c(2, 2)) # plot area for 4 graphs
plot(1 / S, 1 / v, type = "l", main = "Competitive", ylim = c(0, 2))
points(1 / S, 1 / v.comp, type = "l", col = "red")
plot(1 / S, 1 / v, type = "l", main = "Pure", ylim = c(0, 5))
points(1 / S, 1 / v, type = "l", col = "red")
plot(1 / S, 1 / v, type = "l", main = "Mixed", ylim = c(0, 2))
points(1 / S, 1 / v.mixed, type = "l", col = "red")
plot(1 / S, 1 / v, type = "l", main = "Uncompetitive", ylim = c(0, 1))
points(1 / S, 1 / v.incomp, type = "l", col = "red")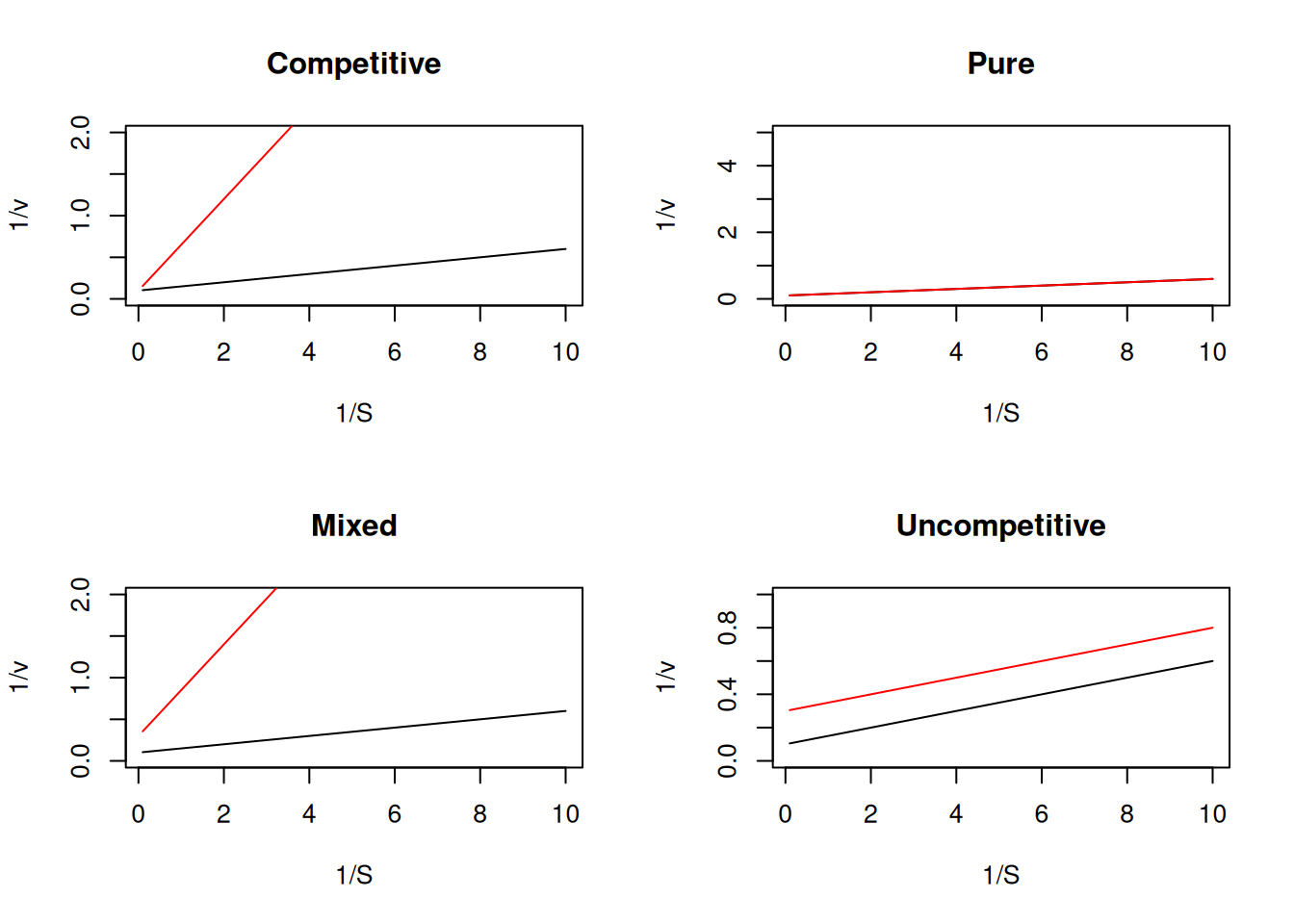
layout(1) # return to normal graphics windowNow the distinction of inhibition models becomes more evident by linearization. As mentioned for the models represented in the direct Michaelis-Mentem equation, one can vary the kinetic parameters and experiment with the visualization of double reciprocals.
Again, although linearization allows a better diagnosis of the type of inhibition present, nonlinear adjustment is more appropriate for determining inhibition constants (Ki’s), since it does not include errors arising from linear transformations (although the insertion of statistical weights can alleviate the imprecision of the results).
Again, although linearization allows a better diagnosis of the type of inhibition present, nonlinear adjustment is more appropriate for determining inhibition constants (Ki’s), since it does not include errors arising from linear transformations (although the insertion of statistical weights can alleviate the imprecision of the results).
Ki & IC\(_{50}\)
The inhibitory concentration at 50% of the inhibitor content, defined as IC\(_{50}\), can be determined empirically without knowledge of the enzyme catalysis parameters involved. To do so, it is enough to obtain a relative inhibition value in a test at a fixed concentration of S, varying the inhibitor content. In fact, analogues to IC\(_{50}\) exist in a wide range in the Natural Sciences, not involving necessarily any kinetic or thermodynamic information of the compounds involved, but only the empirical information of the result. For example, the parameters DE\(_{50}\) (effective dose) or DL\(_{50}\) (lethal dose), and even projections of X\(_{50}\), such as Tm (denaturation temperature at 50%), and the value of pKa in buffers (pH at which the species are 50% ionized/protonated in solution).
However, there is a useful relationship between the inhibitor dissociation equilibrium constant Ki and the value of IC\(_{50}\) that allows their exchange, as long as the inhibition model is known (Yung-Chi and Prusoff 1973). Generalizing to inhibition models, a general equation for the Cheng-Prusoff relation can be defined as:
\[ IC_{50} = \frac{(1+\frac{S}{Km})}{(\frac{1}{Kic})+(\frac{1}{Km*Kiu})} \tag{7}\]
For example, for a competitive inhibition model, where Kiu is zero:
\[ IC_{50} = Kic(1+\frac{S}{Km}) \tag{8}\]
As mentioned above, the value of IC\(_{50}\) can be obtained from experimental data of relative inhibition (v/Vm, for example) at different inhibitor concentrations by setting a value of S. In this case, we can illustrate in
R the obtaining of IC\(_{50}\), using a non-linear fit to the following four-parameter equation (Rodbard curve, DeLean, Munson, and Rodbard (1978)).\[ residual act. \, \% =\frac{v}{Vm} = inf+\frac{sup-inf}{1+log(\frac{I}{IC_{50}})^{nH}}) \] {#eq:eqRodb}
# Non-linear fit to IC50 curve
logI.nM <- c(5.5, 5.2, 4.9, 4.6, 4.3, 3.7, 3.3, 3, 2.8)
# conc. of I, in log10 units
ativ.res <- c(0.02, 0.07, 0.12, 0.22, 0.36, 0.53, 0.67, 0.83, 0.85)
# ativ. residual, v/Vm
data <- data.frame(logI.nM, ativ.res) # create dataframe
plot(ativ.res ~ logI.nM, data) # plot data
ic50.fit <- nls(formula(ativ.res ~ inf + (sup - inf) /
(1 + (logI.nM / logIC50)^nH)),
algorithm = "port", data = data,
start = list(inf = 0, sup = 0.80, logIC50 = 4, nH = 10),
lower = c(inf = -Inf, sup = -Inf,
logIC50 = 0, nH = -Inf)) # nonlinear fit
summary(ic50.fit) # fit summary
Formula: ativ.res ~ inf + (sup - inf)/(1 + (logI.nM/logIC50)^nH)
Parameters:
Estimate Std. Error t value Pr(>|t|)
inf -0.3211 0.2932 -1.095 0.32348
sup 1.1200 0.2311 4.847 0.00469 **
logIC50 4.0807 0.2309 17.675 1.06e-05 ***
nH 4.0540 1.7462 2.322 0.06792 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.02769 on 5 degrees of freedom
Algorithm "port", convergence message: relative convergence (4)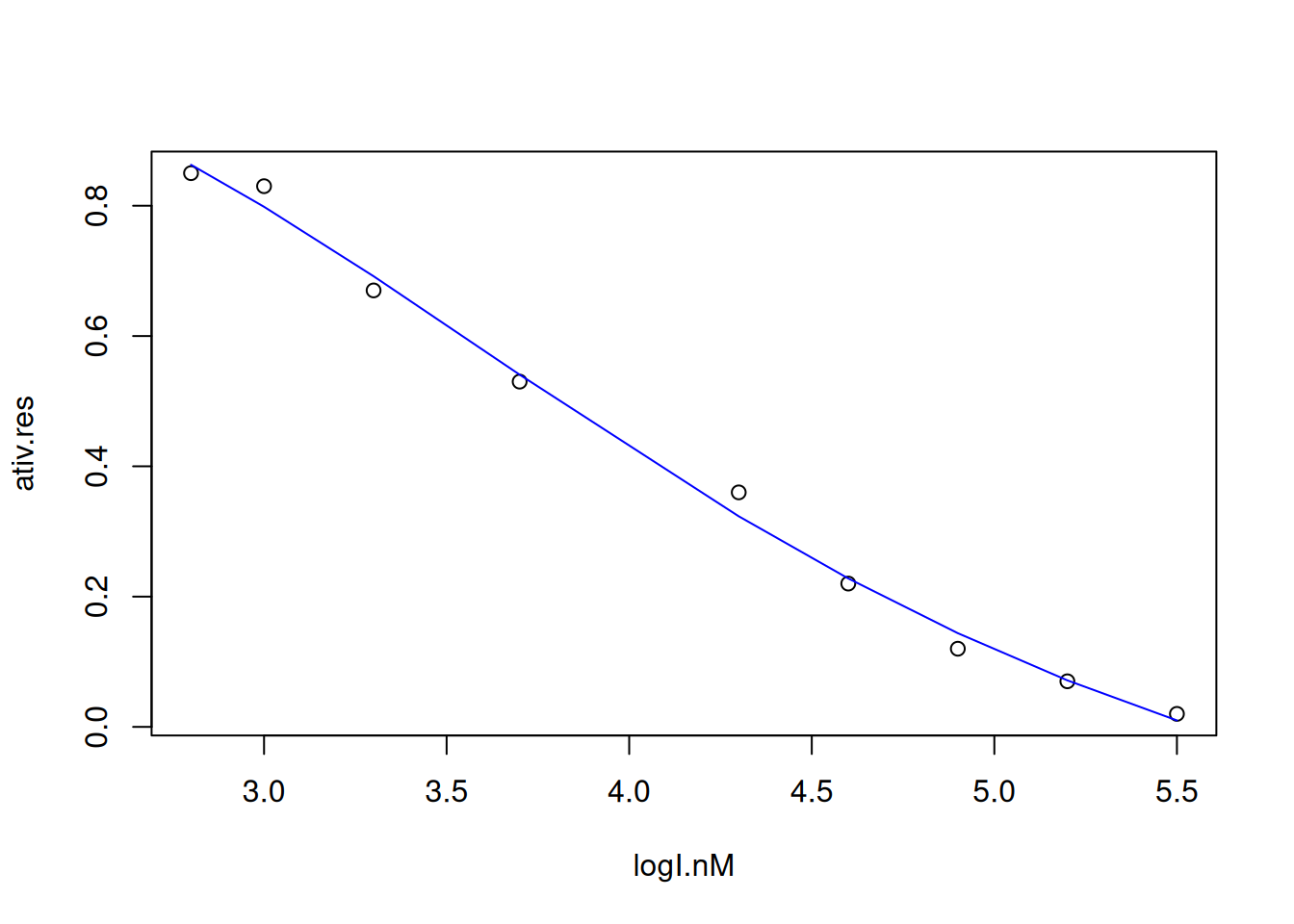lines(logI.nM, fitted(ic50.fit), col = "blue") # fitted line
# And to extract the value of IC50...
IC50 <- 10^(coef(ic50.fit)[3]) # extraction of the 3rd parameter from the
# fitting table, that is: logIC50:
IC50 logIC50
12042.04 Note that the logIC50 parameter was extracted from the nonlinear fitting table by the
To do this, we can use two
coef command. This is very useful when we want to use a coefficient obtained in automatic (programmable) calculations, as we will see later. For now, it is interesting to present the IC50 parameter obtained in a more elegant way.To do this, we can use two
R functions to express quantitative results together with characters (words, sentences): print() and cat. The code snippet below illustrates this output, and some differences.cat("IC50 Value (nM):", IC50, "\n")IC50 Value (nM): 12042.04 print(paste("IC50 Value (nM):", IC50))[1] "IC50 Value (nM): 12042.0403466162"Basically,
print displays quotes and indexes the column name, while cat omits them. In addition, another variation in the printing format between the two commands can be seen in the example below:print(paste("teores:", c(10, 25, 50)))[1] "teores: 10" "teores: 25" "teores: 50"cat("teores:", c(10, 25, 50))teores: 10 25 50Another possibility in
R is to reduce the number of decimal places displayed. In this case, the round command can be used.IC50 <- 10^(coef(ic50.fit)[3])
print(paste("IC50 value (nM):", round(IC50, digits = 2)))[1] "IC50 value (nM): 12042.04"# rounding to two decimal placesOnce again, it is worth highlighting the existence of some useful
R packages for calculating IC50, including the drc package (dose-response curve).Statistical diagnosis of enzyme inhibition
In parallel with the visual inspection of linearization graphs for enzyme inhibition, it is possible to validate one model over another by analyzing the dispersion of model errors. But it is also possible to use the
Mathematically, BIC and AIC can be expressed as:
BIC function or the AIC function of R, which respectively calculate values for the Baysean Information Criterion (Spiess and Neumeyer 2010) or the Akaike Information Criterion (Akaike 1974). In common, these parameters calculate a relative value of information not computed by an evaluated model. The lowest value found for both reflects the solution of the best fitting model.Mathematically, BIC and AIC can be expressed as:
\[ BIC = p*ln(n)-2*ln(RSE)\\ \\ AIC = n*ln(\frac{RSE}{n})+2k+[\frac{2k(k+1)}{n-k-1}])\\ \tag{9}\]
Where p represents the no. of model parameters, n the total number of experimental points, k the factor p+1, and RSE the value of the sum of squares of the residuals (residual sum squares).
To exemplify the use of these quality parameters of the statistical model, one can use a dataset contained in the
nlstools package, providing the fitting, plotting, inspection of residuals, and application of BIC and AIC:# Application of information criteria for fitting kinetic curves
library(nlstools)
comp <- nls(compet_mich, vmkmki, list(Km = 1, Vmax = 20, Ki = 0.5))
# competitive fitting, with data, equation and seeds provided
# by the nlstools package
plotfit(comp, variable = 1) # plotting command of the package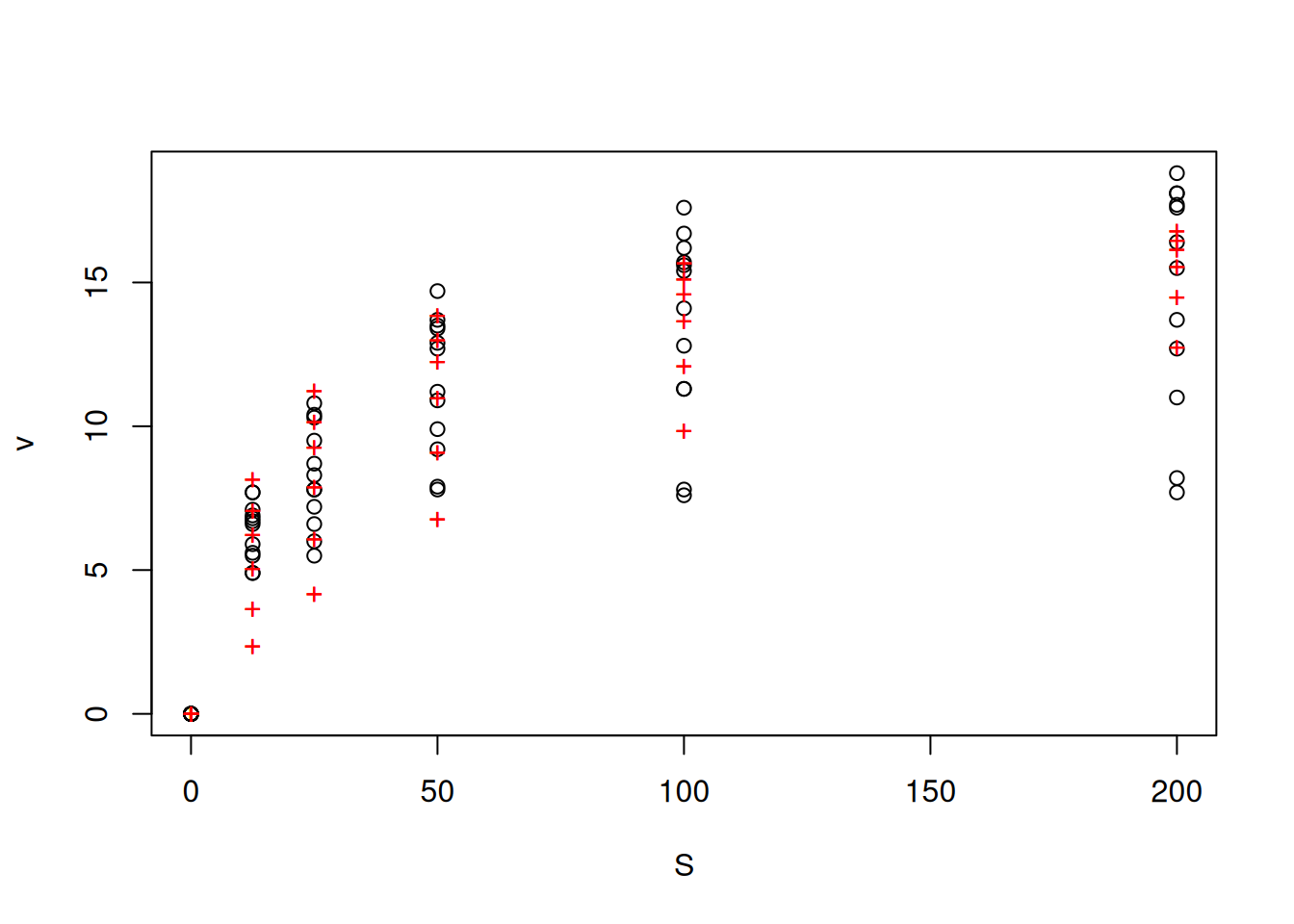
summary(comp)
Formula: v ~ S/(S + Km * (1 + I/Ki)) * Vmax
Parameters:
Estimate Std. Error t value Pr(>|t|)
Km 15.2145 2.5005 6.085 5.79e-08 ***
Vmax 18.0557 0.6288 28.713 < 2e-16 ***
Ki 22.2822 4.9060 4.542 2.30e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.603 on 69 degrees of freedom
Number of iterations to convergence: 11
Achieved convergence tolerance: 5.116e-06res_comp <- nlsResiduals(comp) # residuals of the fit
plot(res_comp, which = 1) # plotting of residuals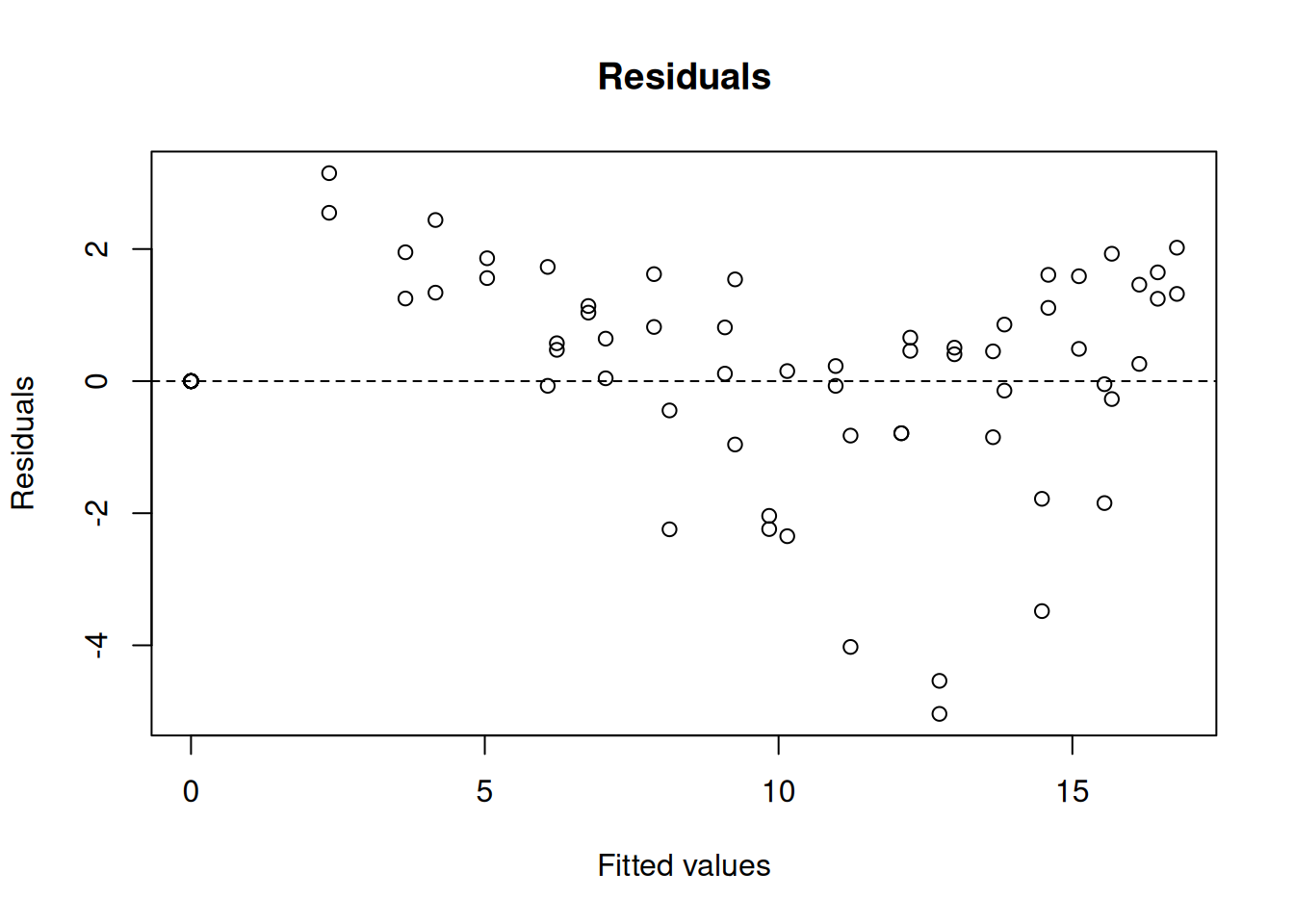
noncomp <- nls(non_compet_mich, vmkmki, list(Km = 1, Vmax = 20, Ki = 0.5))
# same as above, but for the non-competitive model
plotfit(noncomp, variable = 1)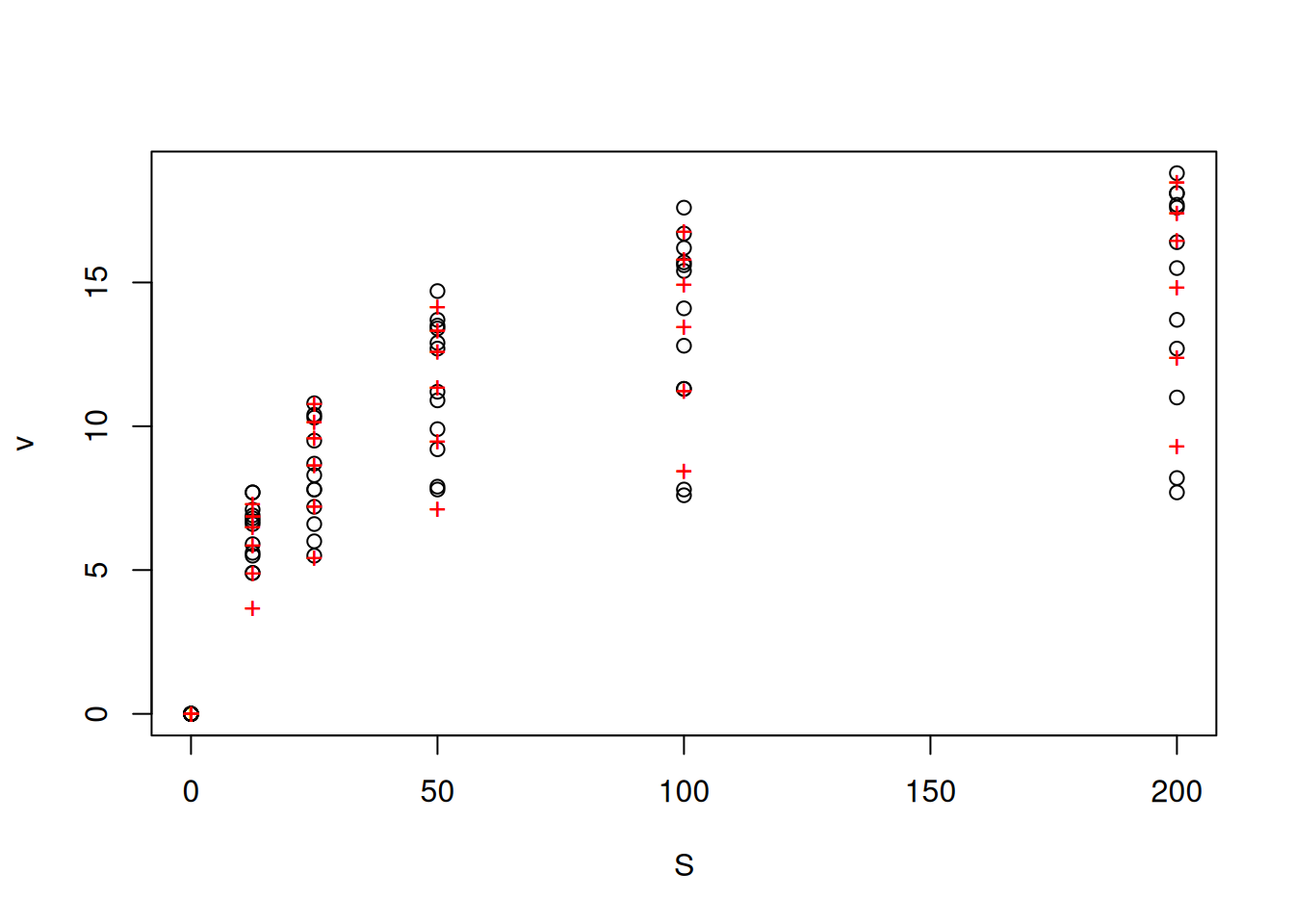
summary(noncomp)
Formula: v ~ S/((S + Km) * (1 + I/Ki)) * Vmax
Parameters:
Estimate Std. Error t value Pr(>|t|)
Km 22.7787 1.4738 15.46 <2e-16 ***
Vmax 20.5867 0.4306 47.80 <2e-16 ***
Ki 101.3563 7.3303 13.83 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8925 on 69 degrees of freedom
Number of iterations to convergence: 7
Achieved convergence tolerance: 8.27e-06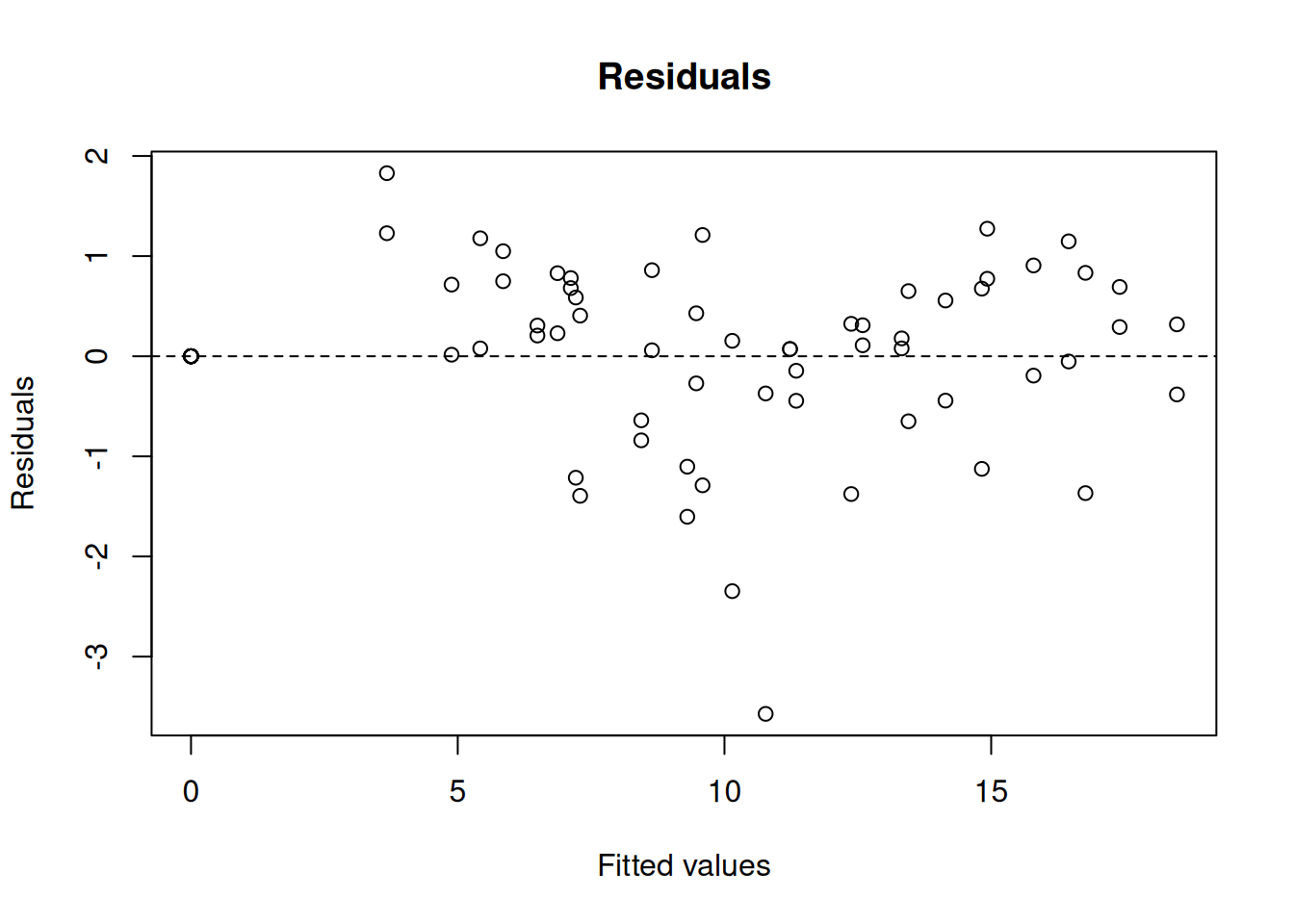res_noncomp <- nlsResiduals(noncomp)
plot(res_noncomp, which = 1)
BIC(comp, noncomp) # Bayesian information criterion df BIC
comp 4 286.2994
noncomp 4 201.9981AIC(comp, noncomp) # Akaike information criterion df AIC
comp 4 277.1928
noncomp 4 192.8915It can be seen in the comparison of the non-linear fits that the non-competitive model fitted better than the competitive model (lower values for BIC and AIC)
Pre-steady state kinetics
There are basically three types of kinetic behavior for enzymes: Henry-Michaelis-Mentem-Briggs-Haldane behavior, succinctly called Michaelian or steady-state behavior, lag-phase behavior (when the substrate takes some time to be converted to product), and burst, transient, or pre-steady-state behavior (when a phase with rapid product release precedes the steady state). Some enzymes work following burst kinetics, including some nucleosidases and glycosidases, and dehalogenases Tang et al. (2003).
Pre-steady-state kinetics follows a slightly different formalism, which depends on the number of reaction steps. Example below for a 3-step reaction (Johnson 1992):
Pre-steady-state kinetics follows a slightly different formalism, which depends on the number of reaction steps. Example below for a 3-step reaction (Johnson 1992):
\[ E+S \begin{array}{c} _{k1}\\ \rightleftharpoons\\ ^{km1} \end{array} E*S \begin{array}{c} _{k2}\\ \rightleftharpoons\\ ^{km2} \end{array} E*P \begin{array}{c} _{k3}\\ \rightarrow \\ ^{}\end{array} E+P \tag{10}\]
In this case, the equations derived from the experimental observations, and which lead to the determination of the rate constants are:
\[ kobs=k2+km2+k3 \tag{11}\]
\[ Ao=\frac{k2*(k2+km2)}{kobs^2} \tag{12}\]
\[ kcat=\frac{k2*k3}{kobs} \tag{13}\]
Where kobs and Ao represent experimental parameters of observed rate constant and amplitude, respectively. These parameters can be obtained from the nonlinear fit of the equation below to the experimental data:
\[ P=Ao(1-e^ {-kobs} + kcat * t) \tag{14}\]
The following code snippet simulates a pre-stationary behavior curve, when the rate constants that determine the experimental parameters are known.
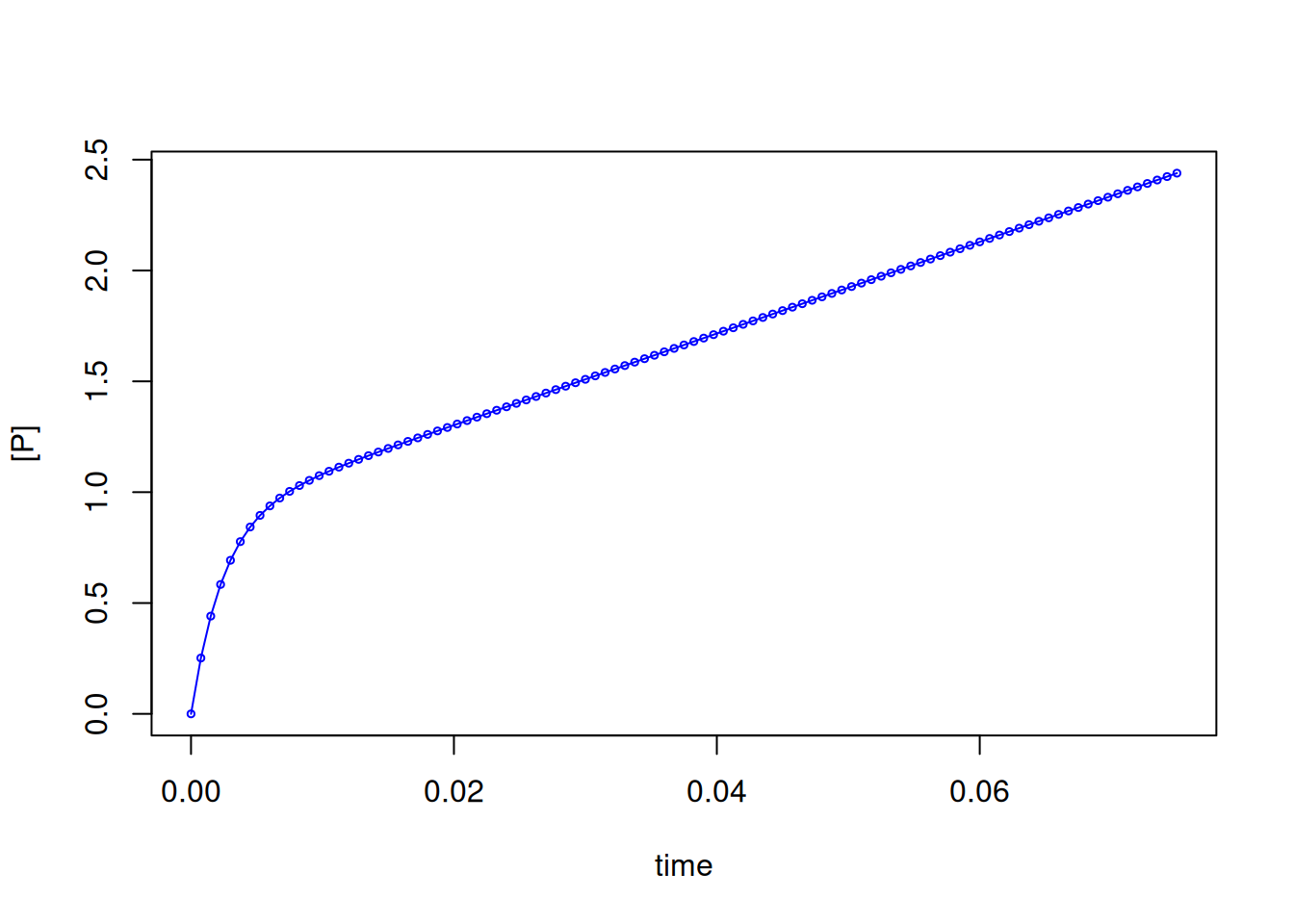
# MM curve in pre-steady state enzyme
# Parameters
k2 <- 387
km2 <- 3
k3 <- 22
xmin <- 0
xmax <- 0.075 # definition of limits for function
# Variables of the simulation equation (function of parameters)
kobs <- k2 + km2 + k3
Ao <- k2 * (k2 + km2) / kobs^2
kcat <- k2 * k3 / kobs
# Definition of the simulation function
sim <- function(x, kobs, Ao, kcat) {
Ao * (1 - exp(-kobs * x)) + kcat * x
}
# Simulation curve
curve(sim(x, kobs = kobs, Ao = Ao, kcat = kcat),
col = "blue",
type = "o", xlim = c(xmin, xmax), cex = 0.5,
xlab = "time", ylab = "[P]"
)
Note from Figure 3 that in transient state kinetics, there is an initial pre-stationary phase that rapidly increases the product content P, and that precedes the stationary phase of constant release of P.
On the other hand, sometimes the opposite is necessary, that is, to determine the rate constants from knowledge of the experimental parameters kobs and Ao. In this case (and in many other transdisciplinary cases)
The procedure involves iteratively minimizing a vector of equations given the seeds for each parameter. To do this, we seek to obtain f(x) = 0 by the difference between a reference value; that is, when the solution finds x when f(x)-y = 0. For example, suppose that f(x) is a+b/x, and that y is 3. Then the search is to find a and b in a+b/x-3.
To determine the rate constants represented in transient kinetics, it is worth mentioning the
In the solution of the parameters for pre-steady state, the use of
R has minimization functions that allow finding the root of linear or nonlinear equations.The procedure involves iteratively minimizing a vector of equations given the seeds for each parameter. To do this, we seek to obtain f(x) = 0 by the difference between a reference value; that is, when the solution finds x when f(x)-y = 0. For example, suppose that f(x) is a+b/x, and that y is 3. Then the search is to find a and b in a+b/x-3.
To determine the rate constants represented in transient kinetics, it is worth mentioning the
optim function in stats or the rootSolve package, which seek to minimize linear and nonlinear equations to find the values of their parameters.In the solution of the parameters for pre-steady state, the use of
R with rootSolve is illustrated below, also adding the search for Km as follows.\[ Km = \frac{k3}{k2+k3} \] {#eq:burstKm}
# Calculation of kinetic constants by solving a system of nonlinear
# equations applied to burst kinetics.
library(rootSolve)
kobs <- 0.06
Ao <- 50
kcat <- 300
Ks <- 15
# defines the nonlinear fitting parameters obtained by progressive curve
# experimental, t x P; # Note: Ks obtained experimentally from the S x kobs curve
# Parameters
# x[1]=k2
# x[2]= k3
# x[3] = Km
# Model
model <- function(x) c(x[1] / kobs^2 - Ao, (x[1] * x[2]) / kobs - kcat,
Ks * x[2] / (x[1] + x[2]) - x[3])
# the model above must contain a list of equations whose equality is zero,
# that is, f(x)=0
(ss <- multiroot(model, c(1, 1, 1))) # rootSolve execution command$root
[1] 0.18000 100.00000 14.97305
$f.root
[1] 0.000000e+00 1.136868e-13 -1.243054e-09
$iter
[1] 4
$estim.precis
[1] 4.143891e-10# (seeds for the algorithm)The results of the minimization can be interpreted as:
- root = values of xi for f(xi)=0 ; that is, k2, k3, and Km; 2. f.root = value of each function for each xi (must be close to zero for each);
- iter = no. iterations;
- esti.precis = precision estimate.
Considering an extensive chapter on enzyme kinetics, there are numerous topics left out, given the main focus of using
R in solving quantitative problems in biophysical chemistry. Thus, we omit several concepts, such as slow kinetics of substrate interaction (slow binding), kinetics of multiple substrates (sequential and ping-pong reactions), integrated Michaelis-Menten equation and progressive curves, activation of modulators, influence of pH and temperature on catalysis, and multisite enzymes, among others.References
Akaike, Hirotugu. 1974. “A New Look at the Statistical Model Identification.” IEEE Transactions on Automatic Control 19 (6): 716–23.
DeLean, A, PJ Munson, and Dl Rodbard. 1978. “Simultaneous Analysis of Families of Sigmoidal Curves: Application to Bioassay, Radioligand Assay, and Physiological Dose-Response Curves.” American Journal of Physiology-Endocrinology And Metabolism 235 (2): E97.
Johnson, Kenneth A. 1992. “1 Transient-State Kinetic Analysis of Enzyme Reaction Pathways.” In The Enzymes, 20:1–61. Elsevier.
Spiess, Andrej-Nikolai, and Natalie Neumeyer. 2010. “An Evaluation of R2 as an Inadequate Measure for Nonlinear Models in Pharmacological and Biochemical Research: A Monte Carlo Approach.” BMC Pharmacology 10 (1): 1–11.
Tang, Lixia, Jeffrey H Lutje Spelberg, Marco W Fraaije, and Dick B Janssen. 2003. “Kinetic Mechanism and Enantioselectivity of Halohydrin Dehalogenase from Agrobacterium Radiobacter.” Biochemistry 42 (18): 5378–86.
Yung-Chi, Cheng, and William H Prusoff. 1973. “Relationship Between the Inhibition Constant (KI) and the Concentration of Inhibitor Which Causes 50 Per Cent Inhibition (I50) of an Enzymatic Reaction.” Biochemical Pharmacology 22 (23): 3099–3108.