1. Choose a topic;
2. Click on the corresponding graph;
3. Click on "Add Plot";
4. Use the mouse for interactivity and/or edit the code.
Reminder: the editor uses infinite undo/redo in the code (Ctrl+Z / Shift+Ctrl+Z) !Interactive Simulations for Biophysical Chemistry with JSPlotly
Instructions
Biophysical chemistry
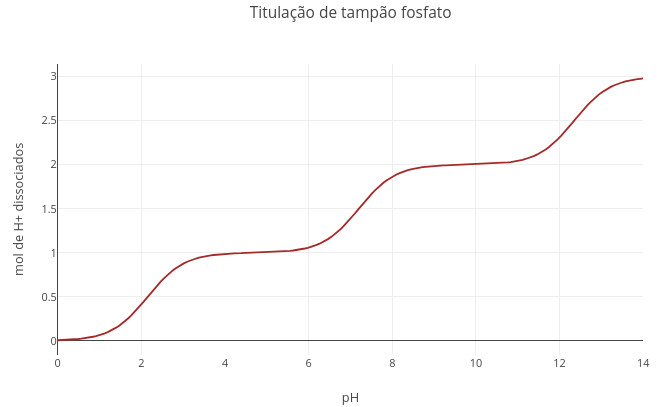
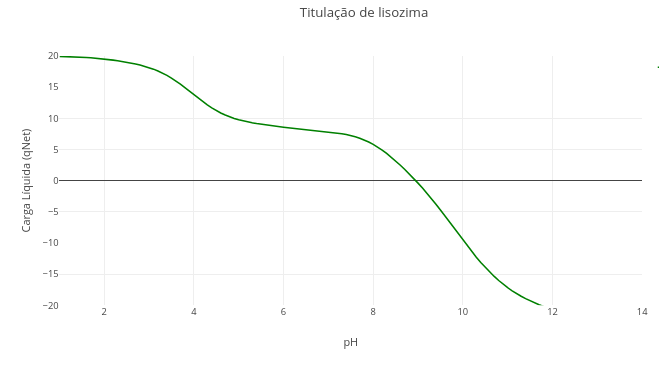
1 Acid-base equilibrium and buffer system
Context:
Equation:
\[
fa= \frac{1}{1 + 10^{pKa1 - pH}} + \frac{1}{1 + 10^{pKa2 - pH}} + \frac{1}{1 + 10^{pKa3 - pH}}
\] Where, fa = fraction of acid (protonatable groups)
Suggestion:
"A. Converting the phosphate buffer (triprotic) curve to bicarbonate buffer (diprotic)"
1. Change the pKa values for the bicarbonate buffer: pKa1 = 6.1, and pKa2 = 10.3;
2. Set a very large value for pKa3 (e.g., 1e20).
3. Click on "add plot."
Explanation: pKa is a term that represents the logarithm of a dissociation constant (-log[Ka]). With an extreme value, the denominator becomes equally large, canceling out the term that carries pKa3. In JavaScript and other languages, "e" represents the notation for power of 10.
"B. Converting the bicarbonate buffer curve to acetate"
1. Simply repeat the above procedure, with pKa1 = 4.75, and eliminating pKa2.
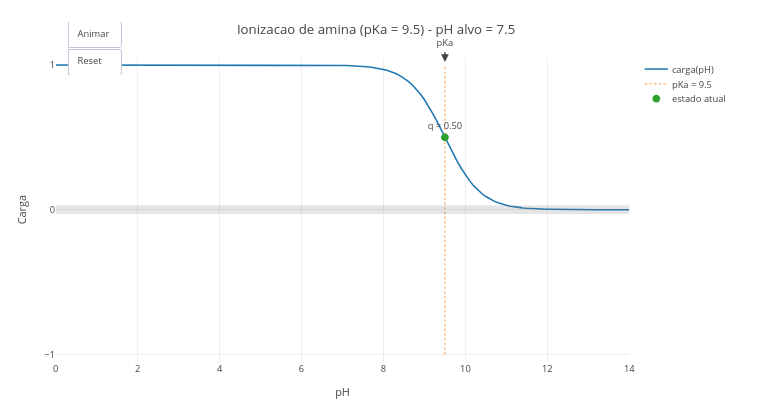
2 Ionization state of biomolecule chemical groups
Context:
Instruction:
After clicking on the related image below, click on “add” and observe the acid-base titration graph generated. The abscissa axis (x-axis) has a wide range of pH values, and the y-axis shows the charge that the molecule with ionization potential manifests at each pH, as a function of its pKa value;
Click on “Animate” to observe the displacement of a small ball along the titration curve, up to a pH value predefined in the simulator script, and as a function of its pKa;
Modify the type of ionizable group (in “let grupo_edit =”) and/or the desired final pH (“let pH_final_edit =”) in the script to evaluate the ionization state of a new group;
Click ‘Reset’ and “Animate” to view the new animation.
Suggestion:
1. Change the pH and the type of group you want to observe;
2. Simulate the ionization state of different molecules, such as drugs with carboxylic acid (e.g., acetylsalicylic acid...aspirin), in blood pH and in the gastric cavity;
3. Create a new ionizable group and predict its ionization state. To do this, simply change the information in 3 constants at the beginning of the script: groups, pKas, and types.
a.
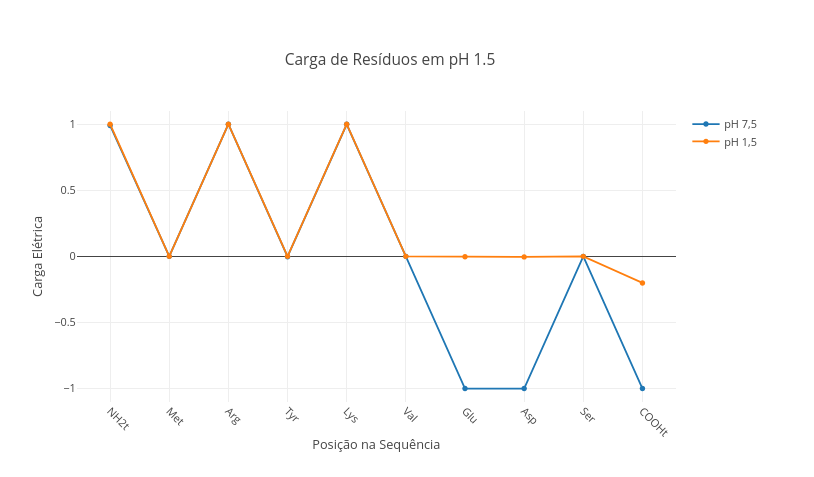
3 Net charge network in peptides
Context:
Equation:
\[
q =
\begin{cases}
-\dfrac{1}{1 + 10^{pK_a - pH}} & \text{(acid group)} \\\\
\dfrac{1}{1 + 10^{pH - pK_a}} & \text{(basic group)}
\end{cases}
\]
Where,
- pKa = base 10 antilogarithm value for the acid dissociation equilibrium constant, Ka (or log[Ka]).
Suggestion:
1. Select the peptide sequence below and observe the charge distribution:
"Ala,Lys,Arg,Leu,Phe,Glu,Cys,Asp,His"
2. Simulate the pH condition of the stomach ("const pH = 1.5"), and check the change in charges in the peptide.
3. Select a physiological peptide (e.g., oxytocin), observe its charge in blood (pH 7.5), and reflect on its potential for electrostatic interaction with cellular components.
"Cys, Tyr, Ile, Gln, Asn, Cys, Pro, Leu, Gly" - oxytocin
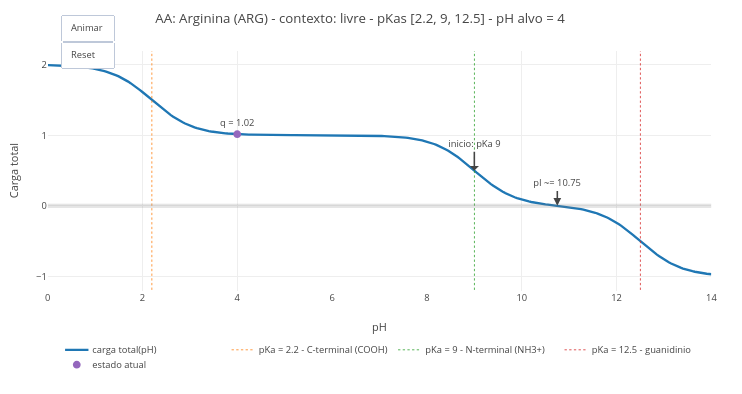
4 Charge, pH, pKa & pI of amino acids (animation)
Context:
Suggestion:
1. Simulate the condition of an amino acid in blood and stomach pH;
2. Compare the pH values of a free amino acid with that of its chain residue;
3. Change the Boolean option in “const showSites” to observe the curves for each ionizable group.
5 Isoelectric Point in Proteins
Context:
Equation: {.unnumbered}
\[
q_{\text{net}}(pH) = \sum_{i=1}^{N} \left[ n_i \cdot q_{B_i} + \frac{n_i}{1 + 10^{pH - pK_{a_i}}} \right]
\]
Where,
- qnet = total net charge;
- qB$_{i} = charge of the basic form for residue i (e.g., +1 for Lys, 0 for Asp);
- n\(_{i}\) = number of groups of residue i.
Suggestion:
"Finding the pI for other proteins"
1. You can check the titration of any other protein or peptide sequence by simply replacing the primary sequence contained in the code. An assertive way to perform this replacement involves:
a. Searching for the "FASTA" sequence of the protein in NCBI ("https://www.ncbi.nlm.nih.gov/protein/") - e.g., ‘papain’;
b. Clicking on "FASTA" and copying the sequence obtained in step 1a;
c. Pasting the sequence into a website for residue quantification (e.g., "https://www.protpi.ch/Calculator/ProteinTool");
4. Replacing the sequence in the code.
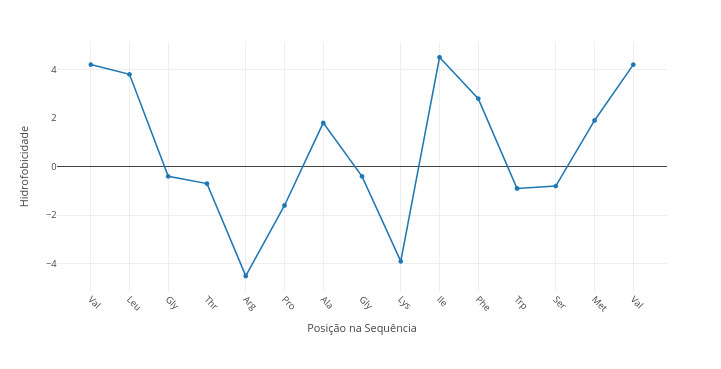
6 Hydrophobicity in amino acid sequences
Context:
Equation:
\[
\tilde{y}_i \;=\; \frac{1}{w} \sum_{k=i-m}^{i+m} y_k,
\qquad w = 2m+1
\]
Where,
\[\begin{aligned} y_i &:\; \text{hydrophobicity value at position $i$ of the sequence} \\ \tilde{y}_i &:\; \text{smoothed value (moving average) at position $i$} \\ m &:\; \text{half-window (number of neighbors on each side)} \\ w &:\; \text{total window width ($w=2m+1$)} \\ i &:\; \text{position of the amino acid in the sequence ($1 \leq i \leq N$)} \end{aligned}\]Suggestion:
1. Try changing the sequence to a known one;
2. Compare a polar sequence with a nonpolar one by overlaying ("add");
3. Transcribe a transmembrane helix sequence of a protein by accessing its data on the PDB website
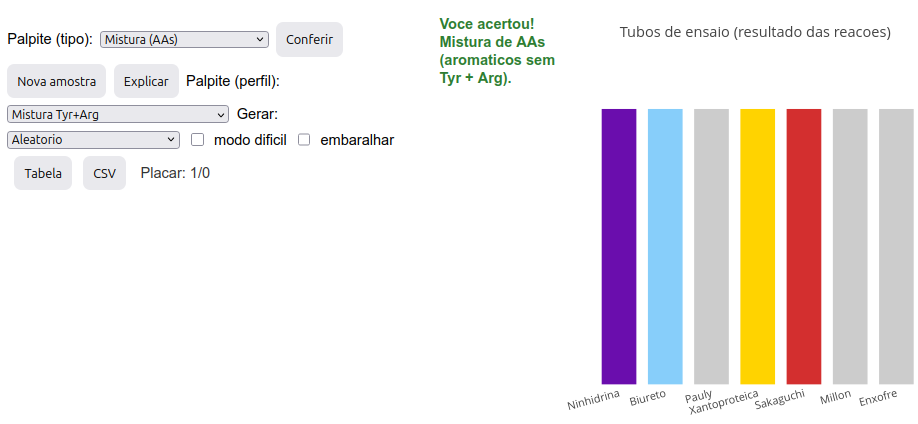
7 Application - Simulated experiment for characterizing amino acids and chains
Context:
Simulator instructions
Option A: discover the nature of a sample:
Click on the image below and select “add.” A set of seven colored bars will be generated, representing the colors obtained in test tubes for seven different reactions for protein characterization: ninhydrin, biuret, Pauly, xanthoprotein, Sakagushi, Millon, and sulfur (Cys).
Discover the type of sample based on the color pattern of the tubes presented, providing a guess. The guess must be by type (in the “Guess (type)” menu - AA, chain, or mixture of AAs) and by profile (in the “Guess (profile)” menu - random, specific AA(s), or specific mixture);
After selecting the 2 menus, click “Check”. If you are correct, a “Score” just below will calculate the number of correct answers/number of samples ‘played’;
If you are wrong, try again or look for an explanation of the color pattern in “Explain”;
There are two other possibilities: “Hard mode,” which hides the names of the reactions while maintaining their sequence, and “Shuffle,” which changes the order of the tubes;
For a new sample, just click on “New sample”;
Option B: discover the color pattern of a reaction for a selected sample:
- Select a sample in “Generate,” and click “New sample.” A set of tubes will be generated with the expected reaction pattern for the sample.
Suggestion:
1. Try clicking on "New sample" to check the frequency of possibilities;
2. Try the two "game" operation options (yes, it's a game... after all, it has a scoreboard!);
3. Try "hard mode" (no reference to reactions in sequence) or "shuffle" (swap the order of reactions). Obviously, however, avoid both simultaneously!
8 Application - ZeMol: a 3D viewer for molecular models
Context:
- models loaded online from the PDB website or PubChem;
- models loaded from the device’s physical memory (PDB, MOL, SDF, XYZ, TXT formats);
- PDB file identification information (or PubChem file name);
- header containing the number of chains, ligands, ions, and disulfide bonds;
- identification of only the \(\alpha\) carbons of each residue of the polypeptide backbone, facilitating model visualization;
- automatic visualization of disulfide bonds;
- identification of residues, ligands, and ions by hovering the mouse over the model;
- checkbox for viewing the secondary structure of proteins (helix, \(\beta\)-sheet);
- checkbox for residue polarity index;
- sliders for CA carbon size (PDB) or atoms in general, and model opacity (useful for highlighting crevices, 2a. structure, carbon chain, ligands, ions);
- hide/show different parts of the model by clicking on its legend (chain, ions, helix/sheets, ligands);
- Highlight AAs (individual, sequence, all of one type, predefined groups in the script);
- Self-sufficient HTML when saving, “freezing” the model in the characteristics you want to present;
- Zoom on mobile devices (one finger fixed on the screen and another dragging the model) and Pan (moving the model with two fingers on the screen) - actions also present in the icons above the model;
- Optional adjustments in the script itself (sizes, colors, thicknesses, AA groups, line type and thickness, for example).
Suggestion:
1. Load a model with PDB code, or a molecule from the PubChem website;
2. If it is a protein, try the separate and combined effects of the sliders for CA size and opacity;
3. Observe the polarity of protein residues in the checkbox of the same name;
4. Try zooming in/out or moving it around the screen with the mouse, or do it on a smartphone as instructed above;
5. Show or hide each chain or all chains, ligands, and ions by clicking on the respective terms in the legend;
6. Select residues of interest in the model, such as catalytic sites, coenzyme binding sites, or activity regulation sites. To do this, type in the corresponding field and click "highlight." Some suggestions:
a. Individual: Arg15, ASP117, 15, A:15, A:ARG15;
b. Ranges: 15-30, A:15-30, Arg15-Asp30;
c. Multiple separated by commas: "Arg15, Asp117";
d. Groups: "aromatic," "polar," "nonpolar," "basic," "acidic," "small."
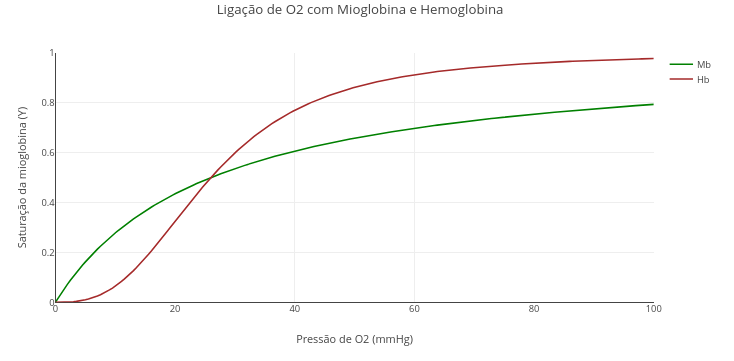
9 Interaction of oxygen with myoglobin and hemoglobin
Context:
Equation:
\[
Y= \frac{pO_2^{nH}}{p_{50}^{nH} + pO_2^{nH}}
\]
Where
- Y = degree of oxygen saturation in the protein;
- pO\(_ {2}\) = oxygen pressure;
- p\(_{50}\) = oxygen pressure at 50% saturation;
- nH = Hill coefficient for the interaction;
Suggestion:
1. Run the application ("add plot"). Note that the value of ‘nH’ for the Hill constant is "1," meaning there is no cooperativity effect.
2. Now replace the value of "nH" with the Hill coefficient for hemoglobin, 2.8, and run again!
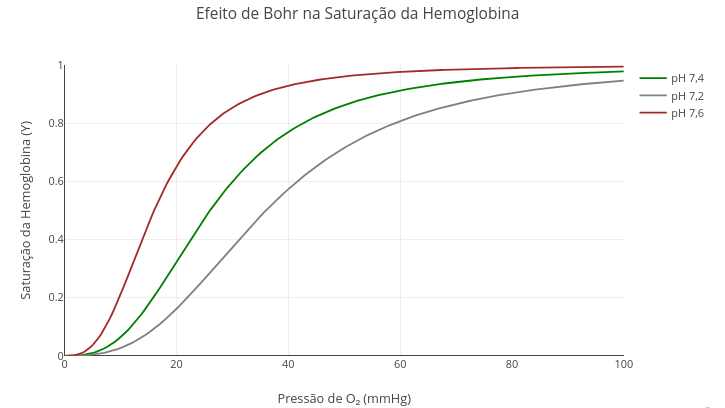
10 Bohr effect on hemoglobin (pH)
Context:
Equation:
\[
Y(pO_2) = \frac{{pO_2^n}}{{P_{50}^n + pO_2^n}}, \quad \text{where } P_{50} = P_{50,\text{ref}} + \alpha (pH_{\text{ref}} - pH)
\]
Where,
- Y = hemoglobin saturation,
- pO₂ = partial pressure of oxygen (in mmHg),
- P₅₀ = pressure of O₂ at which hemoglobin is 50% saturated,
- P\(_{50,ref}\) = 26 mmHg (standard value),
- \(\alpha\) = 50 (intensity of the Bohr effect),
- pH\(_{ref}\) = 7.4,
- n = 2.8 = Hill coefficient for hemoglobin.
1. Try changing the reference pH for the interaction;
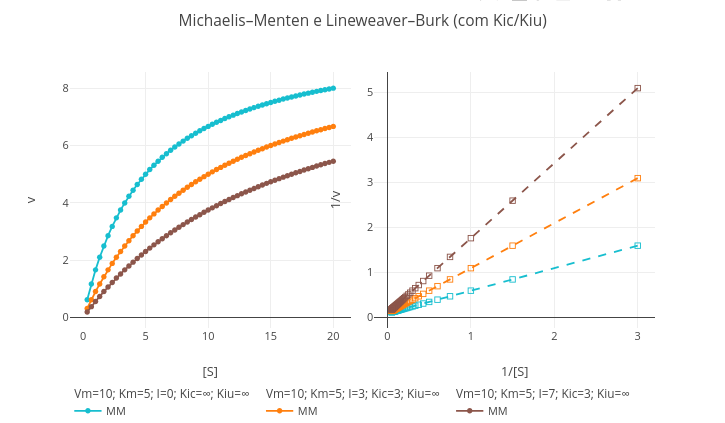
2. Simulate other allosteric models by changing the value of "n"11 Enzyme catalysis and inhibition
Context:
Equation:
\[
v=\frac{Vm*S}{Km(1+\frac{I}{Kic})+S(1+\frac{I}{Kiu})}
\]
Where
- S = substrate content for reaction;
- Vm = reaction limit speed (in books, maximum speed);
- Km = Michaelis-Mentem constant;
- Kic = inhibitor dissociation equilibrium constant for competitive model;
- Kiu = inhibitor dissociation equilibrium constant for noncompetitive model
Suggestion:
"A. Enzymatic catalysis in the absence of inhibitor."
1. Just run the application with the general equation. Note that the values for Kic and Kiu are high (1e20). Thus, with high "dissociation constants," the interaction of the inhibitor with the enzyme is irrelevant, returning the model to the classic Michaelis-Mentem equation.
2. Try changing the values of Vm and Km, comparing graphs.
3. Use the geographic coordinates feature on the icon bar ("Toggle Spike Lines") to consolidate the mathematical meaning of Km, as well as to observe the effect of different values on the graph visualization.
"B. Competitive inhibition model."
1. To observe or compare the Michaelis model with the competitive inhibition model, simply replace the Kic value with a consistent number (e.g., Kic= 3).
"C. Incompetitive inhibition model."
1. The same suggestion above applies to the incompetitive model, this time replacing the value for Kiu.
"D. Pure non-competitive inhibition model."
1. In this model, the simulation is based on equal values for Kic and Kiu.
"E. Mixed non-competitive inhibition model."
1. For this model, simply allocate different values for Kic and Kiu.
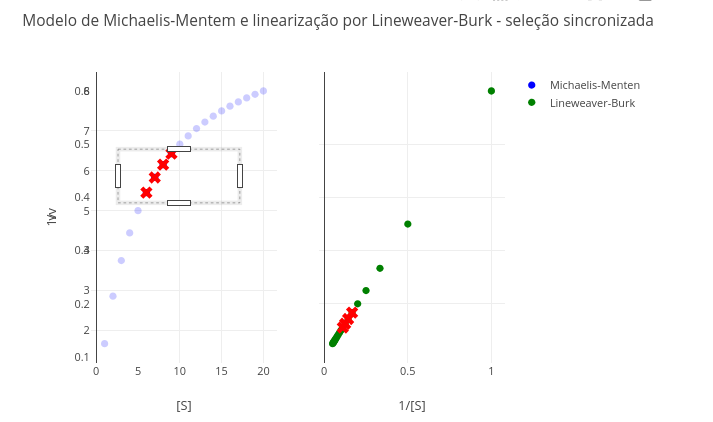
12 Linearization of kinetic data by Lineweaver-Burk
Context
12.1 Equation
\[
\frac{1}{v} = \frac{1}{S}*\frac{Km}{Vm} + \frac{1}{Vm}
\]
Suggestion
1. Try selecting the extremes of the Michaelis-Mentem graph (hyperbolic curve), and observe the same points in the double reciprocal. Which values are more reliable in the latter, the first or the last?
2. Research other forms of linearization (e.g., Eadie-Hofstee; "v/S" X "v"), and see how the transformation and selection of points presents itself. To do this, change the constants below:
const invS = S.map(s => 1/s);
const invV = V.map(v => 1/v);
13 Enzyme Inhibition Diagnosis (Michaelis-Mentem and Lineweaver-Burk)
Context
Suggestion
1. Simulate the conditions for competitive inhibition by entering a value for the inhibitor content ("I") and changing the value of "Km";
2. Do the same for a non-competitive model, but change the value of "Vm";
3. Try the pure non-competitive model by changing "Km" and "Vm" to the same value;
4. Test mixed competitive inhibition by entering different values for "Km" and "Vm".
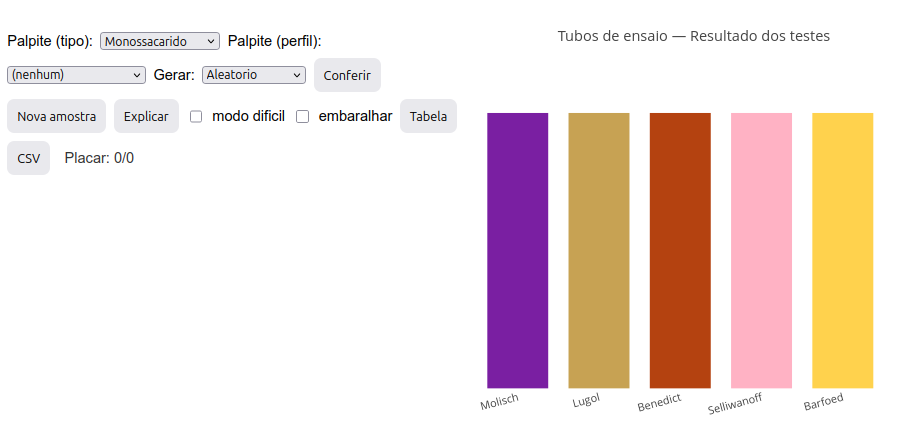
14 Application - Simulated experiment for carbohydrate characterization
Context:
Molish test - detects carbohydrates (purple ring); reaction with \(\alpha\)-naphthol producing furfural or hydroxymethylfurfural;
Lugol’s test (I₂/KI) - detects polysaccharides (dark blue tube);
Benedict’s test - detects reducing monosaccharides (and also lactose); tube with dark orange/brick-colored precipitate;
Selliwanoff test (resorcinol) - differentiates ketoses (red tube) from aldoses (pale pink tube);
Barfoed test - differentiates mono (tube with red precipitate - cuprous oxide) from oligosaccharides (yellowish tube).
Simulator instructions
Option A: discover the nature of a sample:
Click on the image below and select “add”. A set of 5 colored bars will be generated, representing the colors obtained in test tubes for the 5 different reactions for carbohydrate characterization: Molish, Lugol, Benedict, Selliwanoff, and Barfoed.
Discover the type of sample based on the color pattern of the tubes presented, providing a guess. The guess must be by type (in the “Guess (type)” menu - monosaccharide, di-oligosaccharide, polysaccharide, water. And by profile (in the “Guess (profile)” menu - reducing, non-reducing, aldose, ketose, monosaccharide, di-oligosaccharide, and polysaccharide;
After selecting from the two menus, click on “Check”. If you are correct, a “Score” just below will calculate the number of correct answers/number of samples ‘played’;
If you are wrong, try again or look for the explanation of the color pattern in “Explain”;
There are two other possibilities: “Difficult mode,” which hides the names of the reactions while maintaining their sequence, and “Shuffle,” which changes the order of the tubes;
For a new sample, just click on “New sample”;
Option B: discover the color pattern of a reaction for a selected sample:
- Select a sample in “Generate,” and click “New sample.” A set of tubes will be generated with the expected reaction pattern for the sample.
Suggestion:
1. Try clicking on “New sample” to check the frequency of possibilities;
2. Try the two operation options of the “simulator/application/game”);
3. Try “hard mode” (no reference to reactions in sequence) or “shuffle” (permutation of the order of reactions). Obviously, however, avoid both simultaneously!
15 Thermodynamic stability of nucleic acids
Context:
Equation:
\[ y(T) = \frac{1}{1 + e^{-\frac{T - T_m}{\beta}}} \]
Where,
- y(T): fraction of denatured DNA at a given temperature T;
- Tm: transition temperature (melting, temperature at which 50% of molecules are double-stranded and 50% are single-stranded);
- \(\beta\): parameter that adjusts the slope of the curve (affected by trehalose and guanidine).
Note:
- Trehalose as a stabilizer (reduces \(\beta\));
- Guanidine as a denaturant (increases \(\beta\));
[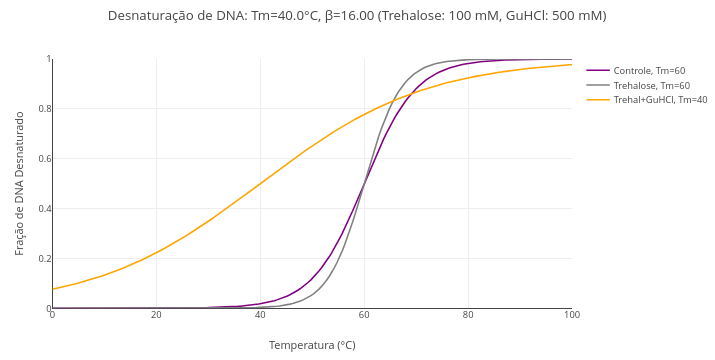 ] (Eq/jsp_denat_DNA_no_osmol.html){target=“_blank”}
] (Eq/jsp_denat_DNA_no_osmol.html){target=“_blank”}
Suggestion:
1. Try testing various conditions involved in the simulation, such as:
a) variation of Tm;
b) variation of the $\beta$ parameter;
c) variation of trehalose content;
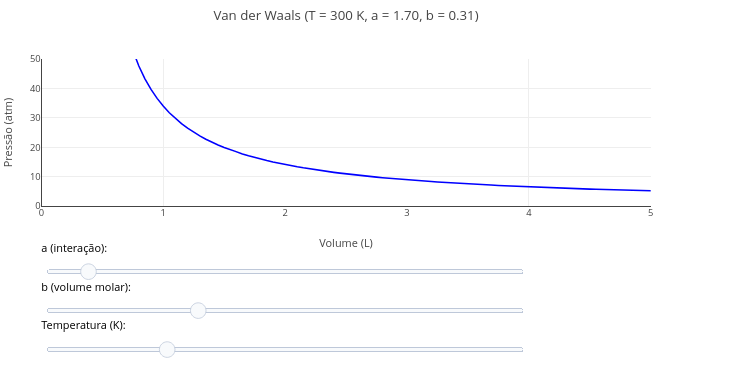
d) variation of guanidine chloride content.16 Van der Waals equation for ideal gases
Context:
Equation:
\[ P = \frac{RT}{V - b} - \frac{a}{V^2} \]
- P = gas pressure (atm);
- V = molar volume (L);
- T = temperature (K);
- R = 0.0821 = ideal gas constant (L·atm/mol·K);
- a = intermolecular attraction constant (L\(^{2}\)·atm/mol$^{2})
- b = excluded volume constant (L/mol)
Suggestion:
1. Try varying the parameters of the equation using the slider for temperature, as well as for coefficients "a and b".
2. Discuss which of the coefficients has the greatest effect on the curve profile, and the reason for this.
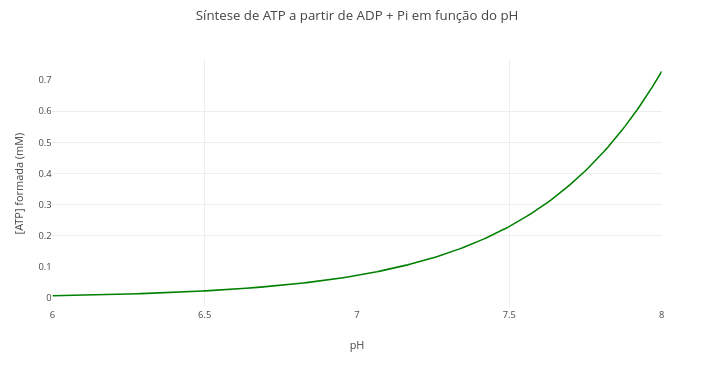
17 Balance of ATP production from reagents, temperature, and pH
Context:
Equation:
\[ \Delta G = \Delta G^{\circ'} + RT \ln\left(\frac{[\text{ADP}] \cdot [\text{P}_i]}{[\text{ATP}]}\right) + 2{,}303 \cdot RT \cdot n_H \cdot \text{pH} \]
Where,
- \(\Delta\)G = Gibbs energy of the reaction (positive for spontaneously unfavorable synthesis, kJ/mol);
- \(\Delta\)G\(^{o'}\) = 30.5 kJ/mol standard biological Gibbs energy for ATP synthesis;
- R = 8.314 J/mol/K (universal gas constant);
- T=310 K (physiological temperature);
- nH\(^ {+}\) = 1 (number of protons involved in the reaction);
- [ADP], [Pi], [ATP] = molar concentrations of reactants and product
Suggestion:
1. Change the quantities involved in the expression and compare with previous visualizations. For example, temperature, pH, and ADP and Pi levels.18 Variation of Gibbs energy with temperature
Context:
Equation:
\[ \Delta G(T) = \Delta H^\circ - T\,\Delta S^\circ + \Delta C_p \left(T - T_0 - T \ln\left(\frac{T}{T_0}\right)\right) \]
Where,
- \(\Delta\)G(T) = Gibbs energy of the reaction at each temperature value, kJ/mol);
- \(\Delta\)H\(^{o}\) = standard enthalpy of the reaction at T\(_{0}\), usually 298 K (J/mol);
- \(\Delta\)S\(^{o}\) = standard entropy of the reaction at T\(_{0}\);
- \(\Delta\)Cp = change in heat capacity of the reaction (J/mol·K), assumed to be constant with temperature;
- T = temperature of interest (K);
- T\(_{0}\) = reference temperature, usually 298 K.
- R = 8.314 J/mol/K (universal gas constant);
Suggestion:
1. Try varying one or more parameters of the expression;
2. Test the behavior of the Gibbs curve at a high reference temperature (simulation for extremophile organism);
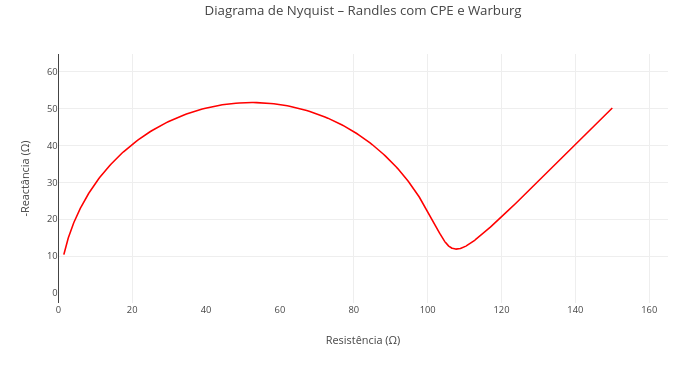
3. Simulate the situation where the variation in heat capacity is zero19 Electrochemical impedance spectroscopy (EIS)
Context:
Equation:
\[ Z_{\text{total}}(\omega) = R_s + \left[ \left( \frac{1}{R_p} + Q (j\omega)^n \right)^{-1} \right] + \frac{\sigma}{\sqrt{\omega}} (1 - j) \]
Where:
- Z\(_{total}\) = total impedance at a given frequency;
- \(\omega\) = Angular frequency (rad/s), \(\omega\)=2πf or \(\omega\)=2πf;
- R\(_{p}\) = Ohmic resistance (resistance of the electrolytic solution, wires, contacts, etc.);
- R\(_{p}\) = Polarization resistance (associated with charge transfer processes, such as electrochemical reactions);
- Q = Constant associated with the constant phase element (CPE), replaces an ideal capacitor to represent non-ideal behaviors;
- n = CPE exponent, between 0 and 1; defines the degree of ideality of the capacitive behavior (n = 1: ideal capacitor; n < 1: dispersion);
- \(\sigma\) = Warburg coefficient, associated with ion diffusion in the electrochemical system;
- j = Imaginary unit, j\(^ {2}\) = −1;
Suggestion
1. Check the effect of Rs on the graph by canceling its value (solution resistance);
2. Observe the deformation of the semicircle by varying the values of the constant phase element (e.g., Q = 1e-3; n = 0.6 - dispersion of capacitive behavior);
2. Try combining other values of the code header parameters to highlight common situations in electroanalysis: Rs, Rp, Q, n, and sigma;
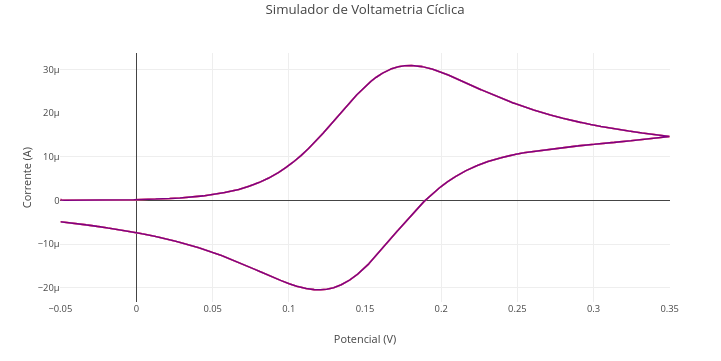
3. Reduce the Warburg model with constant phase element to a simple Randles model, consisting of only two resistors in series, the second in parallel with an ideal capacitor, and without Warburg diffusion (sigma = 0; n = 1).20 Cyclic voltammetry
Context:
Equation:
\[ j = j_0 \left[ \exp\left(\frac{\alpha n F (E - E^0)}{RT}\right) - \exp\left(\frac{-(1 - \alpha) n F (E - E^0)}{RT}\right) \right] \] Where:
- j = current density;
- j\(_{0}\) = exchange current;
- \(\alpha\) = charge transfer coefficient;
- E = potential applied to the electrode;
- E\(^{0}\) = standard electrode potential;
- n = number of electrons;
- F = Faraday constant (96485 C·mol⁻¹)
- R = universal gas constant (8.314 J·mol⁻¹·K⁻¹);
- T = temperature
\[ \frac{\partial C(x,t)} {\partial t} = D \frac{\partial^2 C(x,t)} {\partial x^2} \]
Where:
- C(x,t) = concentration of the electroanalytical species (mol/cm³), as a function of position x and time t;
- D = diffusion coefficient of the species (cm²/s);
- t = time (s);
- x = distance from the electrode surface (cm);
- \(\delta\) = notation for partial derivative.
$$
E = E^0 + ( ) $$
\[ i(t) = n F A D \left. \frac{\partial C(x,t)} {\partial x} \right|_{x=0} \] Where:
- A = electrode surface area (cm²);
- i(t) = current at time t (A, Ampere).
Cyclic Voltametry Simulator
Suggestion:
1. Observe the number of values at the beginning of the code, tangible to "parametric manipulation." Try to understand what they represent, and consciously vary their values, aiming to add value to the learning of the simulation. This is the essence of "parametric manipulation" that involves "reproducible teaching"!21 Diagrams and flowcharts
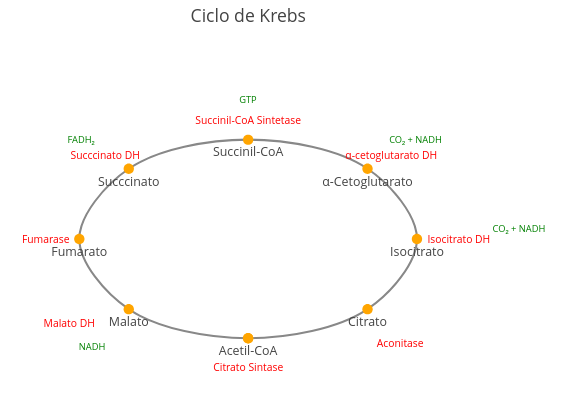
Context: Diagram
Suggestion:
1. Try repositioning enzymes and metabolites by clicking and dragging the terms;
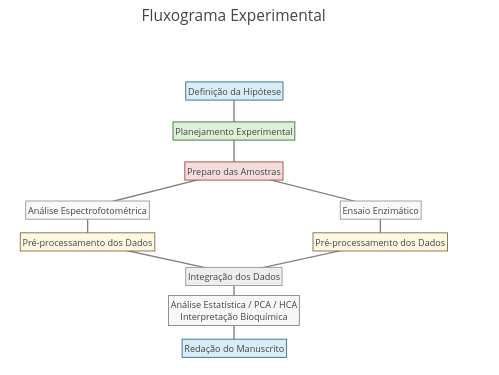
2. Try replacing the names in the code to produce another metabolic cycle, such as the urea cycle.Context: Flowchart
Suggestion:
1. Reposition terms and connectors by dragging them with the mouse;
2. For a different flowchart in the content, modify the terms in the code;
2. For a different flowchart in the format, change the font and connector characteristics in the "annotations" constant.
Data Analysis
22 User data insertion
Context
Suggestion:
1. Try changing the data entered, overlaying the graph or not;
2. Try changing the data representation in "mode" and "type" to points, lines, points+lines, bars.
23 Loading a file for analysis
Context - CSV file
Instructions:
- 1 Click add plot and select a CSV file from the browse button at the top. Note: variable X in the 1st column of the file, and variable Y in the 2nd column;
- Click add plot again to view the resulting graph.
1. Try other CSV files;
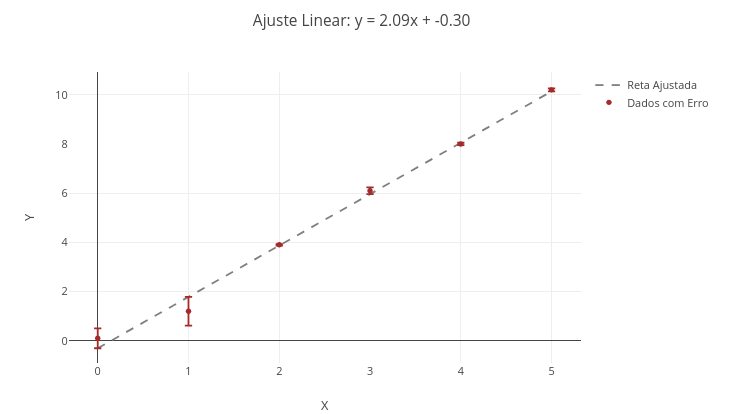
2. Vary the aspects of the graph, such as type, color, marker size, etc.24 Linear data adjustment
Context:
Equation:
\[ y = \alpha x + \beta + \varepsilon \] Where:
- y = dependent variable;
- x = independent variable;
- \(\alpha\) = slope of the adjusted line;
- \(\beta\) = intercept of the adjusted line;
- \(\epsilon\) = measurement error.
\[ \alpha = \frac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - \left( \sum x_i \right)^2} \]
\[ \beta = \frac{\sum y_i - \alpha \sum x_i}{n} \]
\[ \hat{y}_i = \alpha x_i + \beta \]
\[ \varepsilon_i = \left| y_i - \hat{y}_i \right| \]
Suggestion:
1. Show the points overlapping or not overlapping the fit line. For overlap, choose "showPoints = true" and "showLine = true";
2. Change the data and perform a new fit to obtain other parameters of the line.25 Polynomial regression
Context:
25.1 Equation
\[ y = \beta_0 + \beta_1 x + \beta_2 x^2 + \cdots + \beta_g x^g \] | Thus, the Vandermonde matrix is constructed as:
\[ X = \begin{bmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^g \\\\ 1 & x_2 & x_2^2 & \cdots & x_2^g \\\\ \vdots & \vdots & \vdots & & \vdots \\\\ 1 & x_n & x_n^2 & \cdots & x_n^g \end{bmatrix} \]
\[
\boldsymbol{\beta} = (X^T X)^{-1} X^T \mathbf{y}
\]
Where:
- T represents the transposed matrix
Suggestion:
1. Try degree 1 for the polynomial, i.e., a reduction of the treatment to linear adjustment;
2. Change the formatting of labels, colors, sizes, etc., in the code;
3. Overlap some adjustments, edit, and reposition the legend;
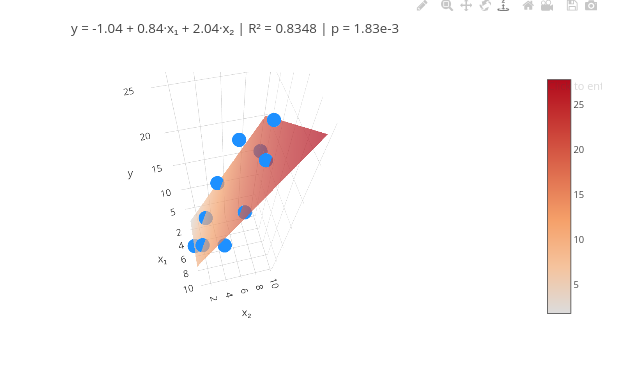
4. Test the code with another data vector.26 Multilinear regression
Context:
Equation:
\[ y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \cdots + \beta_p x_{pi} + \varepsilon_i \]
\[ \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon} \]
\[ \hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y} \]
Where: - \(\beta\) = coefficient vector; - y = response vector; - X = design matrix; - \(\epsilon\) = random noise
\[ \hat{\mathbf{y}} = \mathbf{X} \hat{\boldsymbol{\beta}} \] \[ \mathbf{e} = \mathbf{y} - \hat{\mathbf{y}} \]
Instructions - 1. Note that there is a Boolean flag (showFit) at the beginning of the code: false for data only, and true for the fit. - 2. You can click on add plot to view the data with the flag set to false, followed by another add plot with the flag set to true.
Suggestion:
1. QSAR ("Quantitative Structure-Activity Relationship") results use multilinear adjustment analysis to identify the strength of predictor variables. Try a dataset on the internet that has two variables (e.g., concentration, pH, compound A, B, etc.).
2. For more predictor variables, see the code below !!26.1 Context: Multiple linear adjustment with 3 or more predictor variables
Suggestion:
1. Try varying the number of predictors (xi). To do this:
a. If you want to reduce it, simply remove the desired vector(s) and correct its quantity in the line: "const X = x1.map((_, i)";
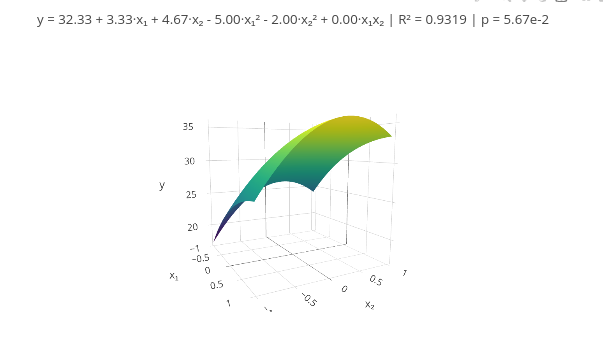
b. If you want to increase it, add a new vector in the corresponding line and update the quantity in the mapping of "const X = x1.map((_, i)".27 Response Surface Methodology (RSM)
Equation:
\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{11} x_1^2 + \beta_{22} x_2^2 + \beta_{12} x_1 x_2 + \varepsilon \]
\[ \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon} \]
\[
\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}
\]
Suggestion:
1. As suggested above, try using data from the literature or another source whose responses are already known, replacing the respective vectors at the beginning of the code. This allows you to compare the effectiveness of using the tool presented.28 Data smoothing - Spline and Savitzky-Golay filter
Context - Cubic spline
\[ S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3 \]
Where:
- S\(_{i}\)(x) = cubic spline function in the interval [xi,xi+1];
- a\(_{i, b\){i}\(, c\){i}\(, d\)_{i}$ = specific coefficients for segment i;
- x\(_{i}\) = starting point of the interval;
- x = independent variable.
28.1 Context - Savitzky-Golay filter
\[ \tilde{y}_i = \sum_{j=-m}^{m} c_j \cdot y_{i+j} \]
Where:
- y\(_{i}\) = smoothed value at position i;
- y\(_ {i+j}\) = actual values of the series within the window;
- c\(_{i}\) = filter coefficients derived from a polynomial regression;
- m = number of points on each side of the central window.
Instructions:
- The code has two true/false flags, one for “useGolay” and another for “useSpline”;
- View the raw data by setting both flags to false;
- To overlay a cubic spline, change its constant to true;
- To overlay the Savitzky-Golay filter, change its constant to true;
- To adjust the filter, modify its parameters in the constants window (sliding window) and/or degree (degree of the polynomial).
Suggestion:
1. Compare the smoothing effects of the two polynomial interpolation treatments;
2. Apply only the filter, adjusting the moving window and polynomial degree parameters;
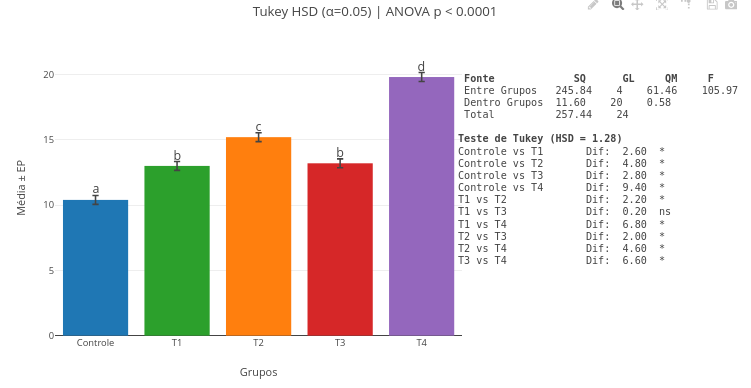
3. Try interpolation with other raw data in the code, replacing the constants "x_values" and "y_raw" constants with numerical vectors;29 ANOVA and Tukey-HSD test
Context:
Equation:
\[ \text{HSD}_{ij} = q_{\alpha} \cdot \sqrt{\frac{\text{MS}_{\text{within}}}{2} \left( \frac{1}{n_i} + \frac{1}{n_j} \right)} \]
Where:
- HSD = minimum value of the difference between two means for it to be considered significant;
- q\(_ {\alpha}\) = critical value of the studentized distribution q (Tukey distribution), depending on the number of groups and the significance level \(\alpha\);
- MS\(_{within}\) = mean square within groups (error) obtained from ANAVA;
- n: number of observations per group (i and j if there are groups of different sizes).
Suggestion:
1. You can click and drag the minimum difference markers (a, b, etc.) above the graph for better visual adjustment, as well as the ANOVA table and the statistical test result;
2. Change the vector values, redo the simultaneous analysis and graph, and notice the difference in the values obtained. Note that, as stated at the bottom, you must refresh the website page to clear previous data retained in the cache;
3. Enter other data in the respective vectors, either your own or from another source;
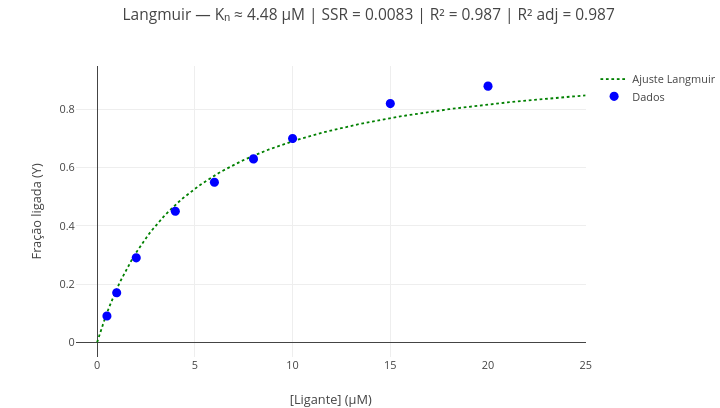
4. Enter new data vectors, or delete some, for a customized calculation and graph.30 Nonlinear data adjustment
Context: Ligand-protein interaction (grid search algorithm)
Equation:
\[ Y = \frac{aX}{K_d + X} \] Where:
- Y = fraction of occupied sites;
- X = concentration of free ligand;
- a = saturation value (sites of the same affinity completely occupied);
- Kd = equilibrium dissociation constant of the complex.
\[ SSR(a, K_d) = \sum_{i=1}^n \left( y_i - \frac{a x_i}{K_d + x_i} \right)^2 \]
Where:
SSR = sum of the squares of the residuals (inversely proportional to the quality of the fit)
Suggestion:
1. As in the previous example, alternately display the points and the adjustment curve using the "Boolean" operation ("showPoints = true/false"; "showCurve = true/false");
2. Change the data and perform a new fit to obtain other parameters of the equation (Kd, SSR, R², adjusted R²). Note: Adjusted R² corresponds to the value of R² corrected for the number of model parameters (in this case, "2"), directly affecting the "degrees of freedom" for the fit.
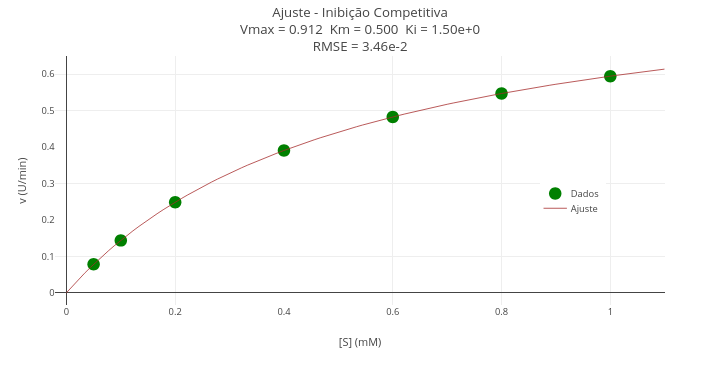
Context - Competitive inhibition in enzyme kinetics (Gauss-Newton algorithm)
Equation:
\[ \theta_{k+1} = \theta_k + \left(J^T J\right)^{-1} J^T \cdot r \]
Instructions
- Note that the code has a flag for true/false in the fit constant. Leave it at false for data representation only (x and y vectors, or S and v);
- In the Plot area of the code, set the trace constant so that it also includes the data vectors;
- Click add plot to view the experimental points;
- To superimpose the fitted curve, update the constants fit and trace (vectors S_fit and v_fit), and choose lines in mode.
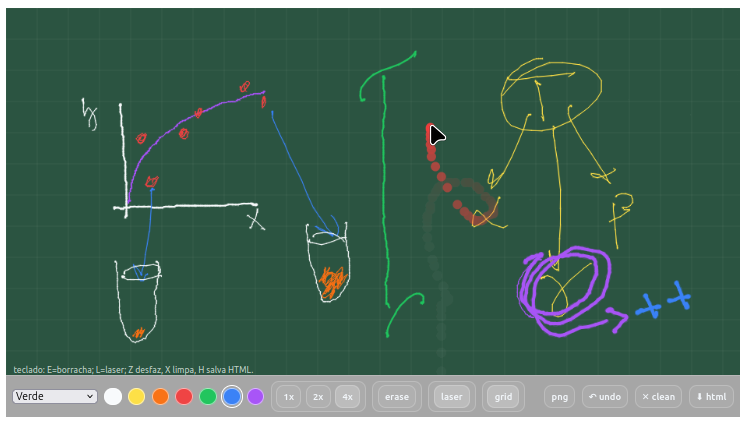
31 Application - Digital Whiteboard
- It can be exported as a self-sufficient HTML file using a button on the whiteboard itself, allowing the generated image to be shared and edited further.
- It allows customization of the code that produces it, allowing you to insert/change pens, thicknesses, and different actions not provided for in the source code.
- Write with 7 colors and 3 different thicknesses;
- Access 4 different colored backgrounds;
- Overlay the plane with a grid;
- Use an eraser;
- Use a laser pointer to locate what you want to highlight;
- Save the image as a PNG, indicating the date and time;
- Undo and clean commands for the board;
- Keyboard shortcuts: E=eraser; L=laser; Z undo, X clean, H save HTML
31.1 Suggestion:
1. You can change the thickness of the pens in "var baseWidth = 1;" ;
2. The 1x, 2x, 4x buttons are multipliers; edit the button creation lines to change the label/multiplier (e.g., "addSize(‘3x’, 3, true)").