Capítulo 8 Membranas
8.1 Concentração micelar crítica (CMC)
A concentração micelar crítica refere-se ao teor de um surfactante mínimo acima do qual esse pode reorganizar-se em micelas ou lipossomos. É bastante utilizado na caracterização de tais compostos, como biosurfactantes na indústria, e pode ser medido por diversas técnicas, incluindo tensão superficial, fluorescência de polarização, turbidimetria e absorção molecular (fotometria).
De modo geral a determinação de cmc é obtida pelo valor da concentração do surfactante no ponto de cruzamento de duas retas obtidas por ajuste linear dos dados em baixo e alto teor do analito, como segue:
\[\begin{equation}
y_1 = y_2 \\
a_1+b_1*x = a_2+b_2*x\\
a_1-a_2 = b_2*x-b_1*x\\
a_1-a_2 = x(b_2-b_1)\\
x = \frac{a_1-a_2}{b2-b1}
\tag{8.1}
\end{equation}\]
De modo geral a determinação de cmc é obtida pelo valor da concentração do surfactante no ponto de cruzamento de duas retas obtidas por ajuste linear dos dados em baixo e alto teor do analito, como segue:
O ponto de intersecção pode ser obtido manualmente, pelo comando locator já referido, ou de forma automática. Nesse caso, o exemplo do R que ilustra esse cálculo baseia-se em resultados de espectrofometria obtidos para um corante, o amarelo ácido 29 (Duff and Giles 1972).
conc<-c(1e-5, 0.00179,0.00357,0.00527,0.00881,0.0106,0.0141,0.0159) # teor do corante (mol/L)
A385 <-c(0.003,0.421,0.712,0.905,1.09,1.17,1.41,1.47) # absorbância em 385 nm
# Gráfico
plot(A385~conc,xlab="[amarelo ácido 29]", ylab="Abs 385")
#Ajuste linear para 2 conjuntos de dados
# 1o. conjunto
linCmc1=lm(A385~conc,subset=(conc<0.007&conc>0)) # 1o. ajuste linear com limites
abline(linCmc1,col="blue", lty="dotted") # linha de regressão
# 2o. conjunto:
linCmc2=lm(A385~conc,subset=(conc<0.02&conc>0.007)) # 2o. ajuste linear com limites
abline(linCmc2,col="blue", lty="dotted") # linha de regressão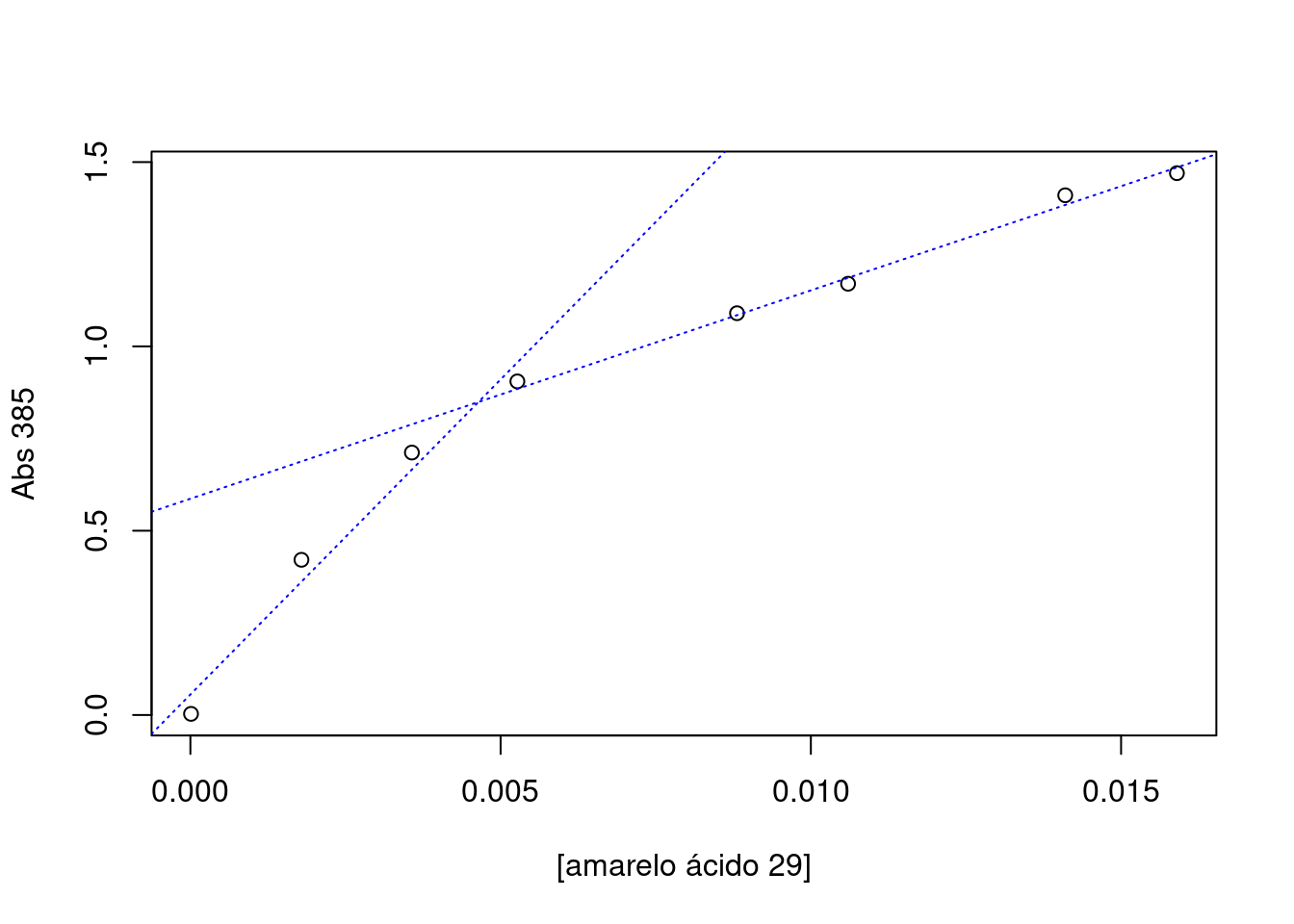
# Cálculo de CMC por intersecção das automática das duas retas:
cmc_auto<-abs((coef(linCmc2)[1]-coef(linCmc1)[1])/(coef(linCmc1)[2]-coef(linCmc2)[2]))
as.numeric(cmc_auto) # fornece o cmc em mol/L## [1] 0.004642773 O valor encontrado pelos autores foi de 0,004 mol/L.
8.2 Transporte em membranas e Teoria Quimiosmótica
O equilíbrio de transporte de solutos por membranas envolve um formalismo que abrange o potencial eletroquímico dos solutos envolvidos, suas concentrações (ou atividade), cargas, potenciais elétricos e volumes parciais em unidade molal. À despeito dessa complexidade, contudo, podemos ilustrar o transporte de íons H⁺ de modo simplificado, seguindo-se a equação abaixo:
\[\begin{equation}
\Delta G_{transp}=2.303(RT*log\frac{H^+_{in}}{H^+_{out}}) + z * F * \Delta \phi
\end{equation}\]
Onde F representa a constante de Faraday, 96485 J\(^{-1}\)\(V^{-1}\)\(mol^{-1}\) (também representado como 1 mol de elétrons), e z a carga do íon equanto que \(\Delta\)\(\phi\) representa a variação de potencial elétrico, e \(\Delta\)pH a variação do valor de pH, ambos obtidos por medições entre o lado interno (matriz mitocondrial) e externo (espaço intermembranas). H\(^{+}\)\(_{in}\) e H\(^{+}\)\(_{out}\) representam o teor de prótons do lado interno e externo da membrana, respectivamente.
Agora, considerando a carga unitária de H⁺ e a definição para pH (-log H⁺),
\[\begin{equation}
\Delta G_{transp}=\Delta \phi * F-2.303RT*\Delta pH
\end{equation}\]
Tangente ao transporte de solutos e íons por membranas celulares, é possível prever-se, por exemplo, o teor de ATP formado durante a fosforilação oxidativa que envolve o retorno de íons H⁺ do espaço intermembranas à matriz mitocondrial. Ilustrando-se, considerando um valor de \(\Delta\)\(\phi\) de 70 mV e um \(\Delta\)pH de 1,4 para as medidas entre matriz e espaço intermembranas mitocondriais, prevê-se a obtenção de ATP pelas relações que seguem, considerando a energia de 31 kJ/mol de ATP :
R = 8.341 # J/mol
T = 298 # K
F = 96485 # constante de Faraday
Dphi = 70e-3 # variação de potencial elétrico in/out membranas
DpH = -1.4 # variação de pH in/out membranas
DG_transp = F*Dphi-2.303*R*T*DpH # equação de transporte
DG_transp_4 = 4 * DG_transp # 4 mol de H+
# Considerando cada mol de ATP para 31 kJ/mol...
DG_transp_4/31e3## [1] 1.905559 Percebe-se, portanto, a produção de 2 mols de ATP nas condições explicitadas.
8.3 Proteínas de transporte em membranas
Enquanto prótons como H\(^{+}\) são transportados em função de seu gradiente de concentração entre o lado interno e externo de membranas, outros compostos e solutos dependem de uma proteína transportadora, como glicose e ácido cítrico. Nesse caso, o transporte não é passivo, mas de difusão facilitada, e seu comportamento cinético pela membrana obedece o formalismo de Michaelis-Menten como segue.
\[\begin{equation}
v_{transp}=\frac{V_{max}*S_{out}}{K_{transp}+S_{out}}
\end{equation}
\]
Onde, analogamente, V\(_{max}\) representa a velocidade máxima (ou limite) de transporte do substrato, S\(_{out}\) o teor do substrato transportado, e K\(_{transp}\) a constante de dissociação do complexo proteína-substrato (ou concentração do substrato a meia saturação do transportador).
References
Duff, DG, and CH Giles. 1972. “Spectrophotometric Determination of the Critical Micelle Concentration of Surfactants.” Journal of Colloid and Interface Science 41 (3): 407–14.